Раздел 2. Математическое описание САР
Структурная схема системы стабилизации и передаточные функции её элементов
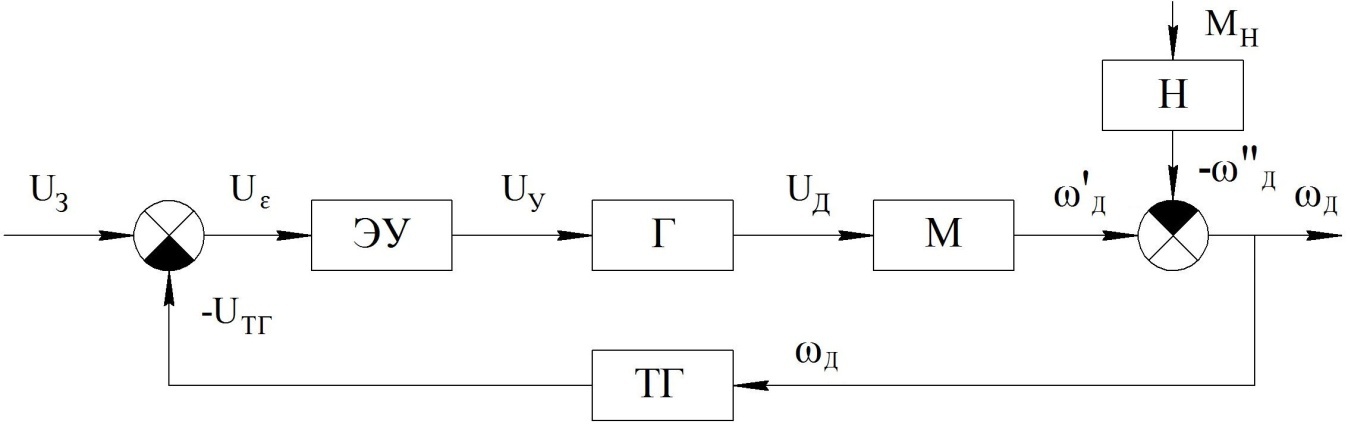
Рис.2. Структурная схема системы стабилизации
Дифференциальные уравнения элементов системы:
1. ЭУ – электронный усилитель
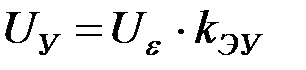
2. Г – генератор
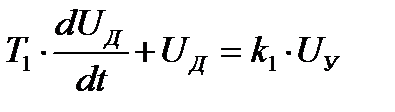
3. М – двигатель постоянного тока
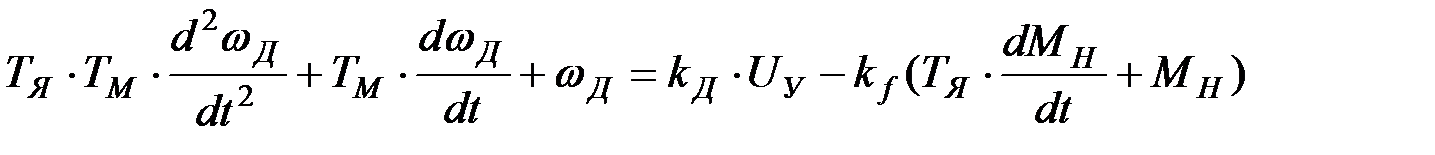
4. ТГ – тахогенератор
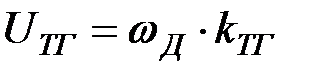
Таблица 1. Исходные данные системы
| № Варианта | Т1 с | Тм с | Тя с | k1 В/в | kД Рад/Вс | kf Рад/ снм | kТГ Вс/ рад | kЭУ В/В | Мсном Н·м | Δωдном рад/с | Δωдст рад/с | ||
| 0.24 | 0.132 | 0.0109 | 3.09 | 1.37 | 3.6 | 0.45 | 13.4 | 1.2 | |||||
| Постоянная времени генератора | Электромеханическая постоянная времени двигателя | Электромагнитная постоянная времени двигателя | Передаточный коэффициент генератора | П.К. Двигателя по управляющему воздействию | П.К. Двигателя по возмущающему воздействию | Передаточный коэффициент тахогенератора | Передаточный коэффициент электронного дви | Номинальный момент сопротивления | Номинальная угловая скорость | Требуемая статическая ошибка системы | |||
Передаточные функции звеньев:
1. WЭУ (p) = 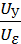 = kЭУ = 10
= kЭУ = 10
2. WГ (p) = 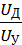 =
= 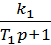 =
= 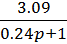
3. WД (p) = 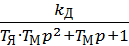 =
= 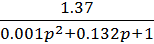
ωД (p) = 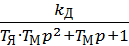
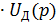 -
- 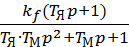
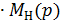
ω'Д (p) = 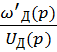 =
= 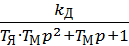 =
= 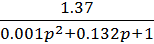
ω''Д (p) = 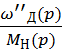 =
= 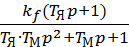 =
= 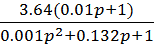
4. WТГ (p) = kТГ = 0.45
Статическая ошибка САР
Передаточная функция разомкнутой системы:
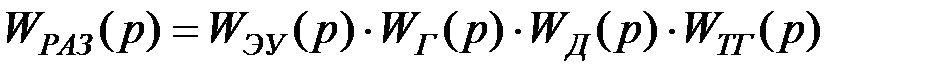
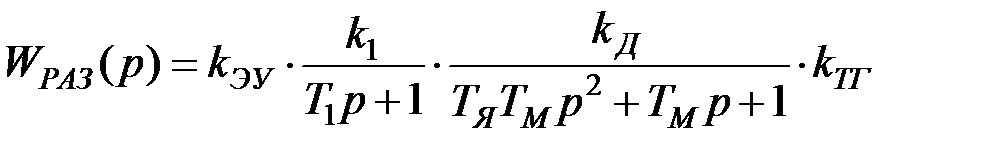
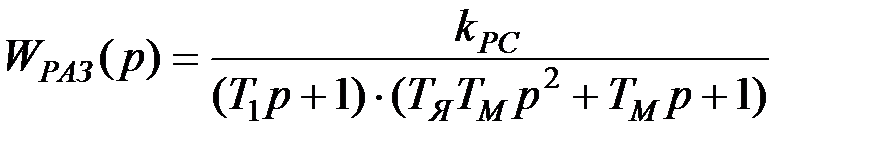
где 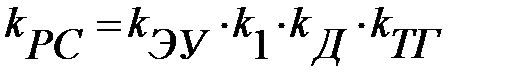 – коэффициент передачи разомкнутой системы.
– коэффициент передачи разомкнутой системы.
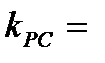 10
10  3.09
3.09  1.37
1.37  0.45 = 19.05
0.45 = 19.05
Статическая ошибка
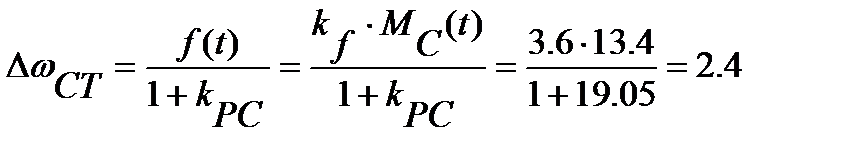
Получили статическую ошибку 2.4, а требуемое (разрешенное) значение 1.2
Вывод: в систему необходимо ввести корректирующее звено.
Раздел 3. Исследование САР без корректирующего звена (КЗ)
Составим структурно-математическую схему системы стабилизации без корректирующего звена, заменив элементы схемы на их передаточные функции (рис.3)
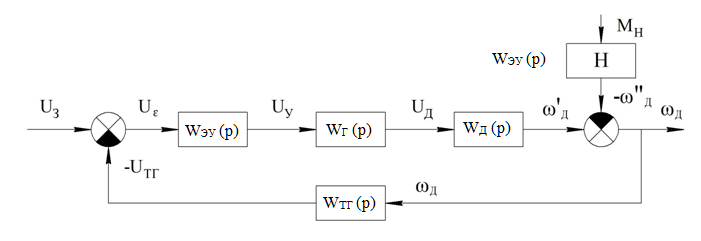
Рис.3. Структурно-математическая схема системы стабилизации без КЗ
Исследование САР по критерию Гурвица
Для исследования устойчивости замкнутой САР по критерию устойчивости Гурвица необходимо составить определитель Гурвица. Для этого понадобится характеристическое уравнение замкнутой системы.
Составим передаточную функцию разомкнутой системы, для чего перемножим все передаточные функции, включая обратную связь.
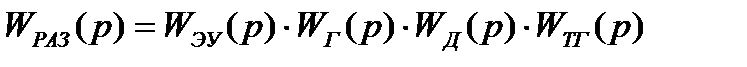
После подстановки численных значений получим:
Wраз (p) = 10 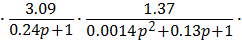 0.45
0.45
Wраз (p) = 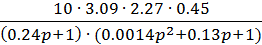 =
= 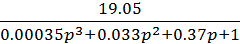
Составим характеристическое уравнение:
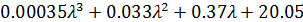
где: a0 = 0.00035, a1 = 0.033, a2 = 0.37, a3 = 20.05
Определитель Гурвица:
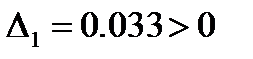
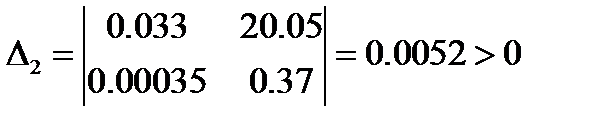
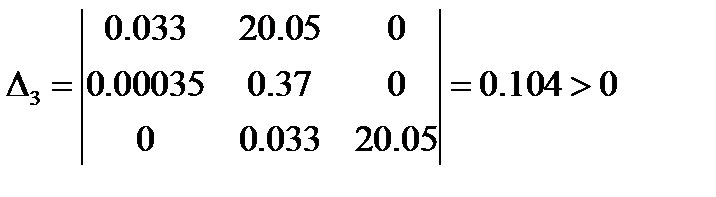
Вывод: система устойчива, так как не имеет отрицательных миноров.
Исследование САР по критерию Михайлова
Wраз (p) = 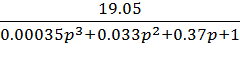
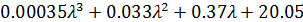 = 0
= 0
Производим замену 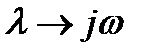
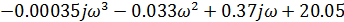 = 0
= 0
UD(𝜔) = 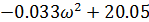
j  VD(𝜔) =
VD(𝜔) = 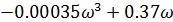
Составим таблицу:
| ω | UD(ω) | i×VD(ω) | ω | UD(ω) | i×VD(ω) |
| 20.05 | 12.62 | 4.77 | |||
| 20.02 | 0.37 | 6.85 | 5.52 | ||
| 19.92 | 0.74 | -0.57 | 5.55 | ||
| 19.75 | 1.11 | -9.65 | 4.68 | ||
| 19.52 | 1.47 | -20.37 | 2.73 | ||
| 19.22 | 1.83 | -32.75 | -0.48 | ||
| 18.86 | 2.18 | -46.77 | -5.13 | ||
| 18.43 | 2.52 | -62.45 | -11.4 | ||
| 17.94 | 2.85 | -80 | -19.47 | ||
| 17.38 | 3.17 | -98.75 | -29.52 | ||
| 16.75 | 3.48 | -119.37 | -41.73 |
Вывод: Система устойчива. Годограф огибает против часовой стрелки начало координат и проходит через 3 квадранта, порядок характеристического уравнения = 3.
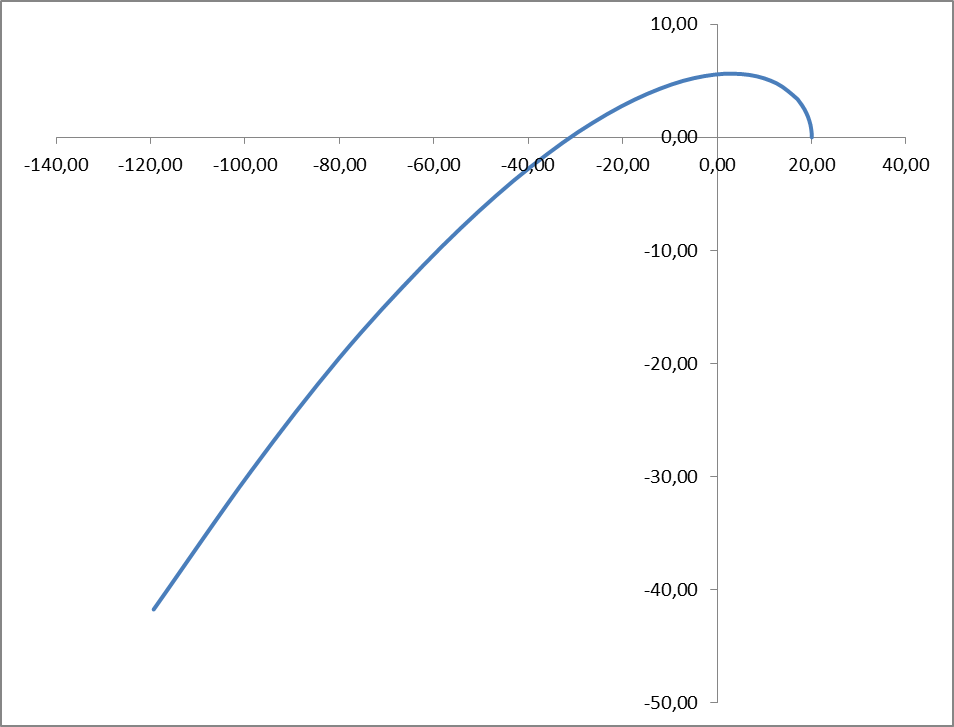
Рис.4. График годографа Михайлова
