Простейшие законы распределения случайной величины
а) Равномерное распределения
Если случайная величина с равной вероятностью может принимать значения в области х1£х£х2, то такое распределение называют равномерным (рисунок 20.2а,б).
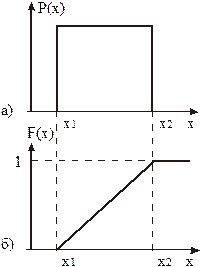 |
Рисунок 20.2
Аналитически функция распределения плотности вероятности и интегральная функция распределения записываются следующим образом:
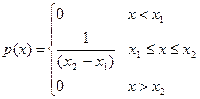  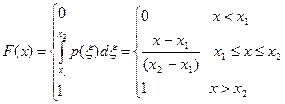 | (20.7) |
Вычисление первого и второго центрального момента по формулам
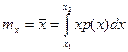 и и 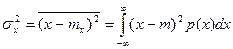 | (20.8) |
приводит к следующим результатам
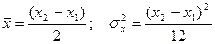 | (20.9) |
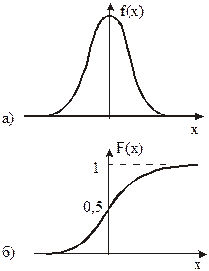 |
б) Гауссово (нормальное распределение).
Рисунок 20.3
Нормальный закон распределения или закон Гаусса играет важную роль во всех практических приложениях теории вероятностей. На рисунке 20.3а,б соответственно, показаны дифференциальная f(x) и интегральная F(x) функции распределения, которые соответственно записываются:
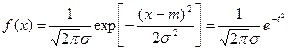 , где , где 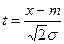 | (20.10) |
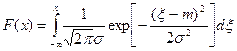 | (20.11) |
Последний интеграл не выражается через элементарные функции. Для него введена специальная функция называемая интегралом вероятности или функцией Лапласа, для которой составлены таблицы. Интеграл вероятности обозначают обычно:
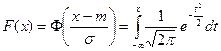 | (20.12) |
Первый начальный и второй центральный моменты, вычисленные по формулам (20.8), для нормального распределения равны:
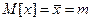 и и 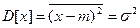 | (20.13) |
т.е. параметры функции распределения имеют смысл математического ожидания и дисперсии. Для нормального распределения справедливо соотношение
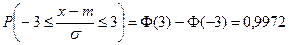 | (20.14) |
т.е. случайная величина с вероятностью 0,9972 не выходит за пределы 3s. Этот способ оценки возможных значений СВ называют правилом «трех сигм» и часто используют при выборе допусков параметров и других расчетов.
в) Распределение Релея.
При решении радиотехнических задач часто встречаются величины распределенные по закону Релея.
Аналитически, распределение Релея записывается в виде:
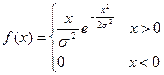 | (20.15) |
График функции f(x) показан на рисунке 20.4.
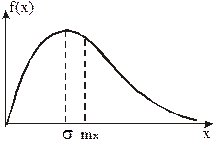 |
Рисунок 20.4
Интегральная функция распределения равна
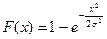 | (20.16) |
Математическое ожидание СВ распределенной по Релею равно
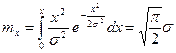 | (20.17) |
Второй начальный момент
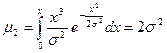 | (20.18) |
Дисперсия СВ х имеет значение
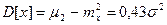 | (20.19) |
Модой функции распределения называют точку, где 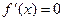 т.е. точку максимума функции f(x). В данном случае
т.е. точку максимума функции f(x). В данном случае
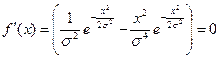 |
откуда имеем
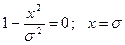 т.е.
т.е. 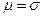
Таким образом, для релеевского закона в отличие от нормального мода функции распределения не совпадает с положением математического ожидания случайной величины.
В статистической радиотехнике часто используются другие распределения – логорифмически нормальное, гамма распределение, c2 – распределение.
Вопросы для самостоятельной подготовки
1. Дайте определения и перечислите свойства интегральной и дифференциальной функции распределения вероятностей.
2. Сформулируйте аксиомы теории вероятностей.
3. В чем разница между математической и эмпирической (выборочной) вероятностями?
4. Какой физический смысл в радиотехнике имеют математическое ожидание и дисперсия случайного процесса?
5. Определить разброс чувствительности приемника содержащего 7 каскадов усиления с одиночными контурами если крутизна транзистора распределена по нормальному закону и имеет среднее значение Y21=10 мА/В и дисперсию sY=2 мА/В, а сопротивление контура Zр=20 кОм; sz=4 кОм, усиление одного каскада определяется по формуле N1=Y21×Zp, а семи каскадов по формуле N=(N1)7. Вычислите минимальное и максимальное усиление приемника и его разброс в пределах трех сигм.
Решение см. П.П.Месяцев. Применение теории вероятностей и математической статистики при конструировании и производстве радиоаппаратуры. М.,Оборонгиз,1958, (стр. 84 пример 82).
