Определители второго и третьего порядков. Их свойства

Понятие определителя вводится только для квадратных матриц. Рассмотрим квадратную матрицу 2^го порядка: .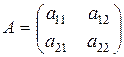

Определение. Определителем 2^го порядка матрицы 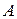называется число:

.

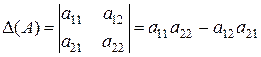Пусть 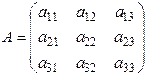– матрица 3^го порядка.

Определение. Минором элемента 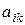называется определитель 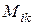, составленный из элементов, оставшихся после вычеркивания из матрицы 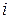-той строки и 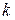-того столбца.

Определение. Алгебраическим дополнением элемента 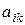называется число

.

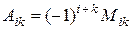Определение. Определителем 3^го порядка (матрицы 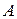) называется сумма произведений элементов первой строки матрицы на их алгебраические дополнения.

.

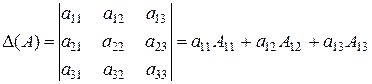В дальнейшем при вычислении определителей мы будем пользоваться более короткой записью.

Определение. Определителем 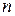-го порядканазывается сумма произведений элементов 1-ой строки на их алгебраические дополнения.

Свойства определителей:

1. Определитель не меняется при транспонировании.

2. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен 0.

3. Если две строки (два столбца) поменять местами, то определитель меняет знак.

4. Если элементы какой-либо строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.

5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен 0.

6. Справедливо равенство

.

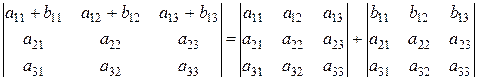7. Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.

8. Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю.

9. Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения другой строки (столбца) равна 0.

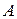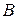Теорема. Если и – квадратные матрицы 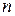-го порядка, то

.

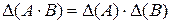Обратная матрица.

Определение. Матрица 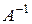называется обратной к квадратной матрице 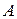, если

.

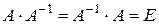Определение. Матрица 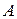называется вырожденной, если 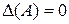; в противном случае

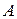– невырожденная матрица.

Теорема.Для того, чтобы матрица 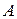имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. .

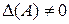В таком случае,

,

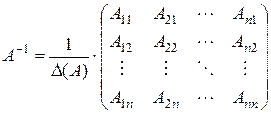т.е. обратная матрица есть разделенная на 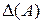транспонированная матрица алгебраических дополнений элементов матрицы .

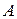Теорема. Есл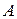и и 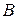невырожденные квадратные матрицы одинакового порядка, то

.

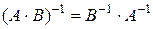Ранг матрица.

Рассмотрим матрицу 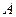размера :

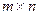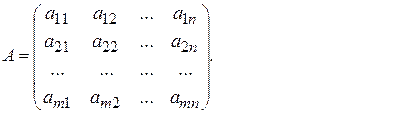
Выберем в матрице 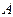произвольно 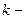строк и 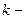столбцов 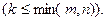Элементы, стоящие на пересечении этих строк и столбцов, составляют матрицу порядка 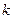. Определитель этой матрицы называется минором 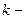го порядка.

Если все миноры 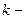го порядка равны нулю, то равны нулю и все миноры более высокого порядка.

Наивысший порядок отличных от нуля миноров матрицы называется рангом этой матрицы ( 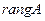или 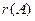).