Иррационал теңдеуді шығару
56. 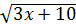 -
- 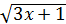 = 1 теңдеуін шешіңіз
= 1 теңдеуін шешіңіз
Шешуі: 1 тәсілі. Екінші (алгебралық) қосылғышты теңдеудің оң жақ бөлігіне шығарсақ, арифметикалық түбір қарастырылғандықтан, оны квадраттауға болады. Квадраттап, ықшамдасақ, 4= 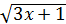 болады. Бұдан х=5. Бұл бастапқы теңдеудің шешімі. Есепті дәрежелеу тәсілімен шештік.
болады. Бұдан х=5. Бұл бастапқы теңдеудің шешімі. Есепті дәрежелеу тәсілімен шештік.
2 тәсілі. 3x+1=y десек, 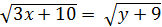 Сонда
Сонда 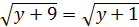
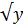 +1
+1 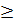 0⇒ (
0⇒ ( 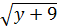 )2= (√y+1)2
)2= (√y+1)2 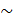 y=16
y=16
Демек, бастапқы белгісізге оралсақ, 3x+1=16⇒ x=5
Бұл ізделінді- х. Есепті белгілеу және дәрежелеумен шештік.
3 тәсілі. Радикалдар қосындысын у деп белгілесек, әрі мұны бастапқы теңдеумен мүшелеп көбейтсек, у=9 болады. Сонда бастапқы теңдеу мына системаға эквивалентті:
+ 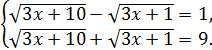
2 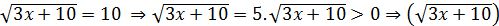 2=25
2=25 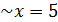
Жауабы: x=5
57. 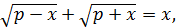 p- нақты оң сан. Теңдеудің оң шешімдерін табу керек.
p- нақты оң сан. Теңдеудің оң шешімдерін табу керек.
Шешуі: 1 тәсіл. Радикалдар айырымын у деп белгілеп, берілген теңдеумен мұны мүшелеп көбейтсек, аралық амалдарды орындағаннан кейін 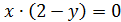 екендігін табуға болады. Бұдан
екендігін табуға болады. Бұдан 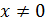 , себебі 2
, себебі 2 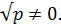 Олай болса y=2. Радикалдар айырымы 2-ге тең болғандықтан, бастапқы теңдеу мына системаға эквивалентті:
Олай болса y=2. Радикалдар айырымы 2-ге тең болғандықтан, бастапқы теңдеу мына системаға эквивалентті:
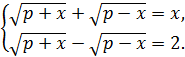
Системаның теңдеулерін біріне-бірін қосу арқылы x = 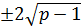 екенін табуға болады.
екенін табуға болады. 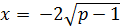 түбірі бастапқы теңдеуді қанағаттандырмайды, себебі теңдеудің оң шешімдері ғана сұралып отыр. p>1 болғанда
түбірі бастапқы теңдеуді қанағаттандырмайды, себебі теңдеудің оң шешімдері ғана сұралып отыр. p>1 болғанда 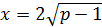 түбірі теңдеуді қанағаттандырады. Демек, осы түбірді зерттеуіміз керек.
түбірі теңдеуді қанағаттандырады. Демек, осы түбірді зерттеуіміз керек.
Теңдеудің түбірлерін зерттеу
Бастапқы теңдеуге зерттелетін түбірді қойып, теңдеуді түрлендіреміз. Бұдан шыққан соңғы өрнек теңдеудің оң жақ бөлігіне тең болуы үшін 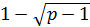 ˂0, яғни p≥2 болуы қажетті және жеткілікті. Сонымен, p≥2 болса, берілген теңдеудің жалғыз ғана
˂0, яғни p≥2 болуы қажетті және жеткілікті. Сонымен, p≥2 болса, берілген теңдеудің жалғыз ғана 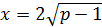 деген шешімі бар. Ал егер 0˂p˂2 болса, теңдеудің шешімі жоқ.
деген шешімі бар. Ал егер 0˂p˂2 болса, теңдеудің шешімі жоқ.
Жауабы: 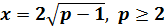
2 тәсіл. Берілген теңдеуді біртіндеп екі рет квадраттасақ, ол x4 - (4-4p)  x2 = 0 теңдеуіне келеді
x2 = 0 теңдеуіне келеді
Бұдан х1=x2=0, x3=2 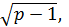 x4= - 2
x4= - 2 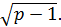 Берілуі бойынша p оң сан болғандықтан, табылған x=0 түбірі бастапқы теңдеуді қанағаттандырмайды, өйткені
Берілуі бойынша p оң сан болғандықтан, табылған x=0 түбірі бастапқы теңдеуді қанағаттандырмайды, өйткені 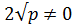 Қалған түбірлерін зерттеу жоғарыда келтірілгендей етіп жүргізіледі.
Қалған түбірлерін зерттеу жоғарыда келтірілгендей етіп жүргізіледі.
58. 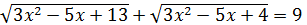 теңдеуін шешіңіз.
теңдеуін шешіңіз.
Шешуі: 1 тәсіл. Радикалдардың түйіндесін у деп белгілеп, берілген теңдеумен мұны мүшелеп көбейтсек, қажетті түрлендірулерден кейін у=1 болады. Түйіндес радикалдың мәні 1 болғандықтан, бастапқы теңдеудің орнына мына ситеманы шешсек болғаны:
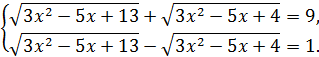
Ескерте кететін бір жағдай, радикал астындағы көпмүшелердің бос мүшеден басқа мүшелері сәйкес келсе, берілген теңдеудің түйіндесін белгілеп, бастапқы теңдеуді онымен эквивалентті системамен алмастырамыз. Система теңдеулерін өзара қосу, не біреуінен екіншісінен азайту арқылы шешуге болады. Қай амалдың тиімділігі радикал астындағы (кіші) бос мүшеге байланысты. Әрине, басқаша жағдайда да есепті шешуге болады. Бұл есепті жоғарыда көрсетілген тәсілдердің бірімен де шешуге болады.
Екінші ескертетін бір жай түйіндес радикалдар әрқашанда сан ретінде табыла бермейді, ол бастапқы белгісізбен де өрнектелуі мүмкін. Көрсетілген тәсілмен барлық есептерді шешуге болады деген ойдан аулақ болу керек, өйткені жалпы жағдайда иррационал теңдеулерді шешу мәселесі табылған жоқ. Сондықтан көрсетілген тәсіл тек кейбір есептерді шешуге жарамды. Иррационал теңдеулерді шешкенде дәрежелеу т.б көмекші түрлендірулер жүргізудің салдарынан бөгде түбір пайда болуы мүмкін. Сондықтан иррационал теңдеулерді шешкенде оқушылар теңдеудегі белгісіздердің қабылдай алатын мүмкін мәндері мен табылған шешімдерді тексеріп отыруды әдетке айналдыру керек.
Үшінші ескертетін жағдай, бұл тәсілді басқа типті есептерді шешуге пайдаланып көруге болады, мысалы алгебралық теңдеулер системасына, т.б.
Түйіндестер тәсілі анық болу үшін тағы да мысалдар келтірелік:
59. 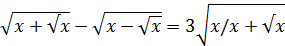 / 2 теңдеуін шешіңіз
/ 2 теңдеуін шешіңіз
Шешуі: 1 тәсілі.
х 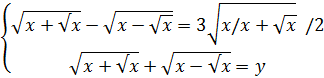
. 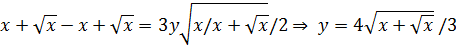
Сонда
+ 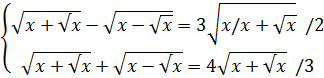
2 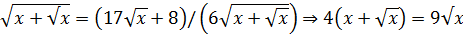
4 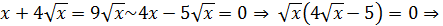 x1=0, x 2=25/16
x1=0, x 2=25/16
Жауабы: x=25/16
2 тәсілі.Белгісіздіңмүмкінмәндержиыны х≥1 теңсіздігіменанықталады. Берілгентеңдеудіортақбөлімгекелтірсек,
2 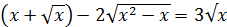
Қатынасы шығады. Бұдан 2 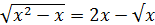 болып, х≥1 шарты орындалғанда, соңғы теңдеудің екі жақ бөлігіде оң сан. Демек оны квадраттауға болады. Квадраттап ықшамдасақ,
болып, х≥1 шарты орындалғанда, соңғы теңдеудің екі жақ бөлігіде оң сан. Демек оны квадраттауға болады. Квадраттап ықшамдасақ,
x (4 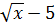 )=0
)=0
Бұдан х1 =0, x2=25/16 х2-нің мәндері ғана анықталу облысында жатыр, оны тексеру бастапқы теңдеудің шешімі ---- ендігін көрсетеді.
60. 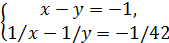
системасын шешіңіз.
Шешуі: 1 тәсілі. Системаның екінші теңдеуінен x-y=xy/42 және х-у=-1 екенін ескерсек, ху=42 болады.
Сонда
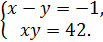
Егер x+y=c десек, бастапқы системаның бірінші теңдеуін алсақ, с-ні табуға болады.
± 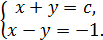
x 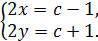
4xy=c2-1. xy=42
екенін ескерсек, с2=169.Бұданc=±13. демек,x1=6, x2=-7, y1=7, y2= -6.
Жауабы: 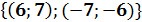
2 тәсілі.Берілгенсистеманыңбіртеңдеуіненбірбелгісіздітауыпалып, екіншісінеқоюарқылы да шешугеболады.
Жаттығулар.
61. 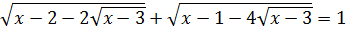
Нұсқау. Әуелі 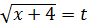 деп белгілеп, бастапқы теңдеуді түрлендіргеннен кейін түйіндесін жаңа белгісізбен белгілеңіз.
деп белгілеп, бастапқы теңдеуді түрлендіргеннен кейін түйіндесін жаңа белгісізбен белгілеңіз.
Жауабы: 4˂х≤7.
62. 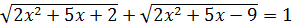
Жауабы: 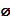
63. 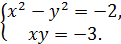
Системасын шешіңіз.
Нұсқау. 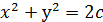 деп алыңыз.
деп алыңыз.
64. 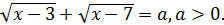
Нұсқау. Радикалдарды белгілеу арқылы да шешуге болады.
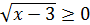 және
және 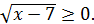
Егер бірінші радикалды у, ал екінші радикалды z десек, онда
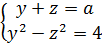
системасына келтіруге болады. Мұнан y=(a+4/а) /2, z= (a-4/а) /2 екенін табамыз. x-ке оралып,
x-(a2+12a+4) /4а
екенін табамыз.
Параметрлі зерттеу.
z ≥ 0 ⇒ a – 4 / a ≥ 0 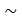 a2 ≥ 4 ⇒ a ≥ 2.
a2 ≥ 4 ⇒ a ≥ 2.
Сонымен,
x=(a2+12a+4)/4a, a≥2, a 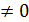
65. 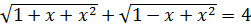
Нұсқау. Есепті түбірдің біреуінен жекелеу, сосын дәрежелеу арқылы да шешуге болады. Көптеген есептер осы тәсілмен шешіледі. Теңдеудің сол жақ бөлігінің екінші қосылғышын оң жағына шығарып екі рет квадраттағаннан кейін x = ±4 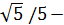 шешімін табамыз
шешімін табамыз
