Метод суммирования значений всех показателей

Оценка 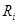каждого подразделения i получается по формуле:

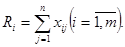(1)

Данным методом пользуются в случае одинаковой направленности исходных показателей и их общей сопоставимости (например, все показатели выражены в процентах выполнения плана). Наилучшее подразделение определяется по максимальной сумме показателей-стимуляторов и по минимальной сумме показателей-дестимуляторов. 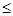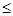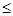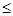Таким образом, критерии оценки наилучшего подразделения для показателей-стимуляторов – max R_i (1 i m), а для показателей-дестимуляторов – min R_i (1 i m).

Метод суммы мест

По исходным данным (матрице Х и вектору S) строится вспомогательная матрица Р по следующим правилам:

а) при s_i = +1 элементы столбца j матрицы Х упорядочиваются по убыванию и элементу 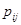придается значение, соответствующее месту элемента 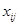среди упорядоченных элементов j-ого столбца;

б) при s_i = -1 элементы столбца j матрицы Х упорядочиваются по возрастанию и элементу 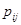придается значение, соответствующее месту элемента 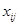среди упорядоченных элементов j-ого столбца.

Таким образом, по каждому j-му показателю объекты упорядочиваются по значениям этого показателя. Оценка R_i каждого подразделения i вычисляется по формуле:

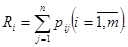(2)

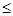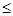Критерий оценки наилучшего подразделения: min R_i (1 i m).

Метод суммы баллов

При построении балльных оценок, кроме исходных данных о значениях показателей, задаются шкалы для оценки каждого показателя. Наиболее распространенными являются непрерывные и дискретные шкалы. Они характеризуются минимальным и максимальным количеством баллов, которыми может быть оценен показатель. Верхняя и нижняя границы шкалы могут иметь как положительное, так и отрицательное значение.

Дискретная шкала задает определенное число уровней оценок (баллов), с помощью которых оценивается показатель. Как правило, в этом случае выбираются целочисленные балльные оценки. Например, показатель производительности труда может оцениваться одним из шести чисел: 0,1,2,3,4,5, а качество продукции – одним из трех чисел: 0,1,2.

В случае непрерывной шкалы оценки могут принадлежать любой точке некоторого отрезка, который определяет шкалу данного показателя. Например, показатель выполнения плана по выпуску продукции может оцениваться десятибалльной непрерывной шкалой, то есть оценки выбираются из отрезка [0,10] и могут быть любыми числами, принадлежащими этому отрезку.

Существуют следующие способы исчисления балльной оценки для конкретного значения показателя:

· непрерывное отображение отрезка, в пределах которого изменяется данный показатель на заданную шкалу;

· с помощью задания интервалов изменения показателя и соответствующих балльных оценок.

Предположим, что известны значения показателей (матрица Х), шкалы оценок по каждому показателю и способы оценки. Тогда можно построить вспомогательную матрицу В, где элементы матрицы – балльные оценки соответствующих показателей. Оценка R_i каждого подразделения i вычисляется по формуле:

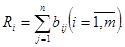(3)

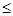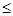Критерий оценки наилучшего подразделения: max R_i (1 i m).

Относительную значимость показателей в рассматриваемом методе можно задавать с помощью соответствующих нижних и верхних границ в шкалах оценок. Метод суммы баллов требует разработки большого числа шкальных оценок, которые необходимо согласовывать между собой.

Метод расстояний

В данном методе, помимо информации о показателях (х), коэффициентах сравнительной значимости показателей 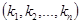и характеристик направления действия показателей 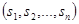, требуется определить по имеющейся информации подразделение-эталон. Это реально не существующее подразделение характеризуется наилучшими значениями по каждому показателю среди всех имеющихся. Показатели подразделения-эталона 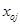строятся следующим образом:

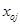= max 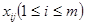при s_j = +1;

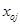= min 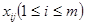при s_j = -1.

В каждом столбце матрицы Х находится наилучшее значение показателя; найденные значения образуют дополнительную строку чисел 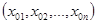- показателей подразделения-эталона.

Оценка R_i каждого i-ого подразделения вычисляется как квадрат расстояний между двумя точками в m-мерном пространстве, координаты первой – это значения показателей подразделения-эталона, а координаты второй – показатели подразделений i.

R_i вычисляется по формуле:

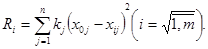(4)

Для вычисления «действительного» расстояния между точками m-мерного пространства необходимо извлечь квадратный корень из всех величин 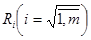, но, как правило, это действие не производится, поскольку оно не влияет на упорядоченность оценок.

Коэффициенты сравнительной значимости k_j необходимы для придания веса различным показателям в соответствии с их важностью. Чем больше k_j, тем более значим показатель j, тем в большей степени отклонение от эталона будет влиять на общую суммарную оценку R_i.

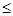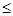Критерий оценки наилучшего подразделения: min R_i (1 i m).

Метод расстояний наиболее формализованный из рассмотренных выше. Он легко позволяет учитывать значимость показателей, и его идея определения оценок как расстояний между точками-подразделениями и точкой-эталоном весьма убедительна.

Вместе с тем и этот методом имеет ряд недостатков:

1. Процедура вычислений сложна, а результаты не столь наглядны.

2. Сама по себе процедура оценки нуждается в совершенствовании: вариации различных показателей могут существенно отличаться, а это означает, что показатели с большей вариацией будут иметь больший вес в суммарной оценке, и, следовательно, неявно они получают преимущество по сравнению с другими показателями.

Сложность и не наглядность метода, возможно, и могут служить препятствием для его широкого применения, но в научных исследованиях на первый план выдвигаются требования обоснованности и логической непротиворечивости метода.