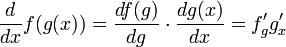Определение производной функции, ее геометрический смысл

Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием.

Определение

Пусть в некоторой окрестности точки 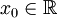определена функция 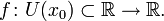Производной функции f в точке x₀ называется предел, если он существует,

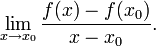
Общепринятые обозначения производной функции y = f(x) в точке x₀:

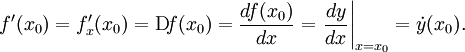
Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

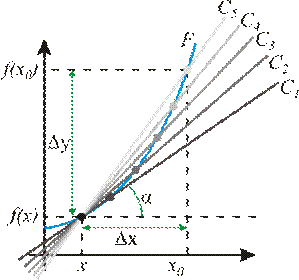
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло серая линия C). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₀ — C₅). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция 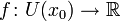имеет конечную производную в точке x₀, то в окрестности U(x₀) её можно приблизить линейной функцией

f_l(x) = f(x₀) + f'(x₀)(x − x₀).

Функция f_l называется касательной к f в точке x₀. Число f'(x₀) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Правила дифференцирования функций

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.

• (f + g)' = f' + g' (производная суммы равна сумме производных)
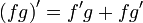• (отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу)
• 
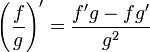
• Если функция задана параметрически:

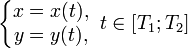, то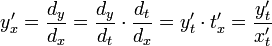

• 

Следующие свойства производной служат дополнением к правилам дифференцирования:

• если функция дифференцируема на интервале (a,b), то она непрерывна на интервале (a,b);
• если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f'(x) = 0 (это так называемая лемма Ферма);
• производная данной функции единственна, но у разных функций могут быть одинаковые производные.

Понятие дифференциала функции, свойства дифференциала функции