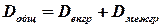Групповая и общая средние
Допустим, что все значения количественного признака X разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.
Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
Общей средней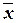 
называют среднее арифметическое значений признака, принадлежащих всей совокупности.
Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.
Выборочная дисперсия
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения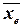 
, вводят сводную характеристику - выборочную дисперсию.
Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения :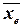
.
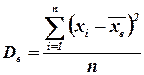Формула для вычисления дисперсии
Теорема. Дисперсия равна среднему квадратов значений признака минус квадрат общей средней:
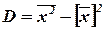
Групповая, внутри групповая, межгрупповая и общая дисперсии
Допустим, что все значения количественного признака X разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю (см. § 6) и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
,
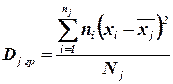где ni - частота значения хi; j - номер группы;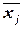 
- групповая средняя группы j; 
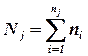- объем группы j.
Зная дисперсию каждой группы, можно найти их среднюю арифметическую.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
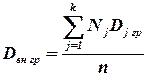
где Nj — объем группы j;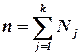 
- объем всей совокупности.
Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
,
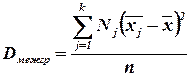где 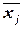- групповая средняя группы j; Nj—объем группы j; 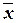- общая средняя; 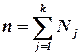- объем всей совокупности.
Теперь целесообразно ввести специальный термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
,
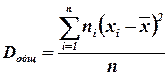где ni - частота значения хi ; 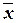- общая средняя; п — объем всей совокупности.
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
