Оценки математического ожидания и среднего квадратического отклонения нормально распределенного признака

1. Для оценки математического ожидания М (Х) = а нормально распределенного признака по выборочной средней и известному среднему квадратическому отклонению 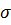служит следующий доверительный интервал:

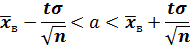
где значение аргумента интегральной функции Лапласа (в таблице № 2).

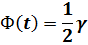
2. При исправленном среднем квадратическом отклонении S получим:

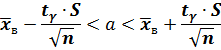
где 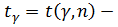значения в таблице № 3.

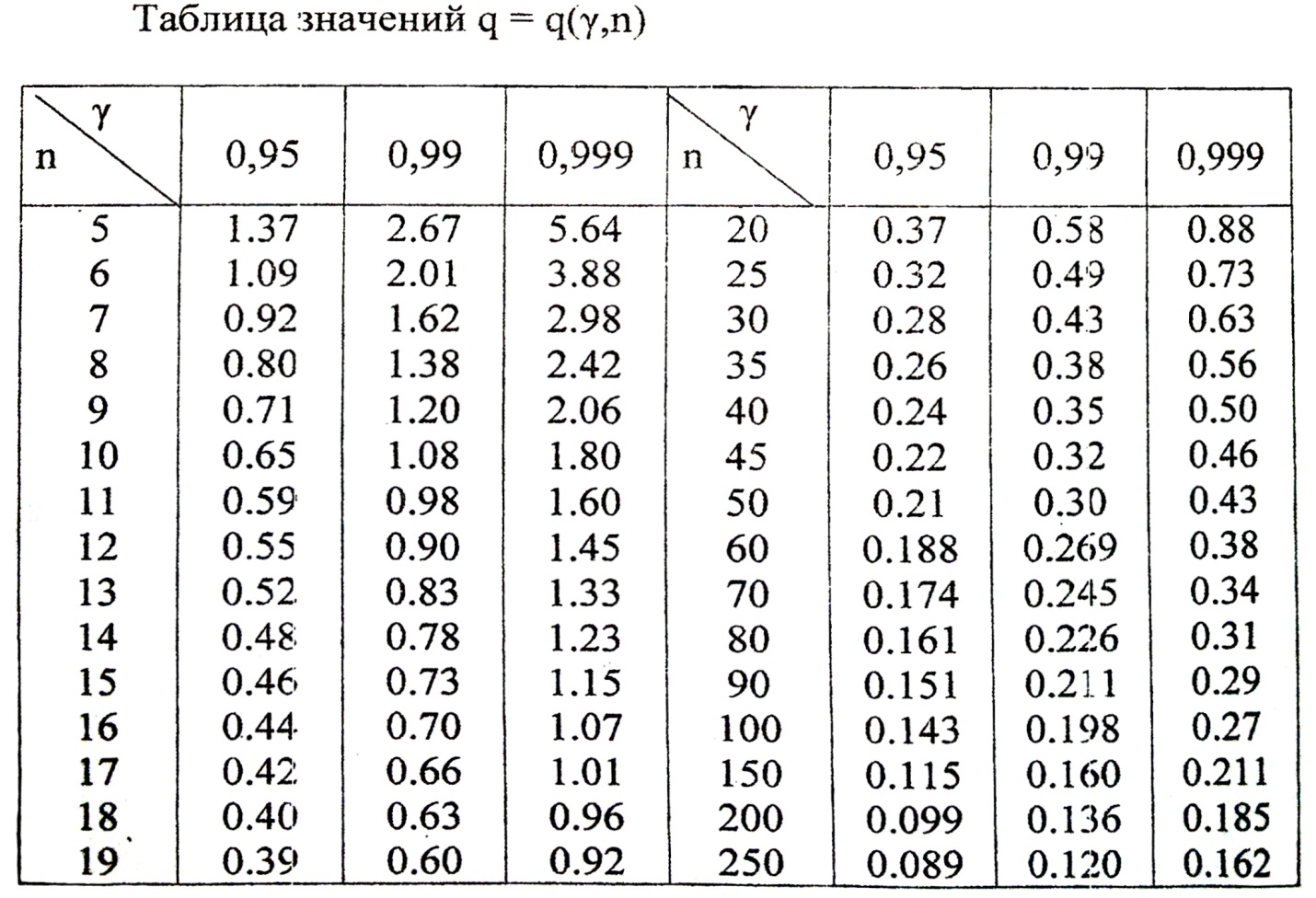
3. Доверительный интервал для оценки среднего квадратического отклонения 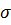при большом числе измерений 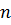имеет вид:

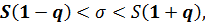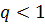при ,

при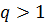

где 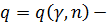значения в таблице № 4.

Пример 1.

Задана выборка значений признака X, имеющего нормальное распределение:

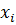	‒2

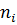Найти: а) выборочную среднюю 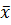и исправленное среднее квадратическое отклонение s; б) указать доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание а признака X; в) указать доверительный интервал, покрывающий с надежностью 0,95 среднее квадратическое отклонение 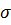признака X.

Решение:

а) Вычисляем объем выборки: .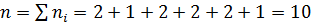

Тогда

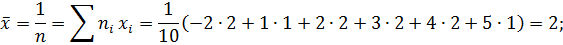
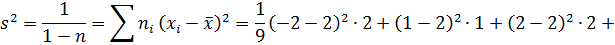
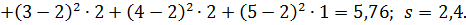
б) Искомый доверительный интервал для математического ожидания а имеет вид:

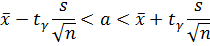
где 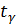находим по таблице приложения 2. При 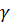= 0,95 n = 10 получаем 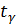= 2,26. Тогда

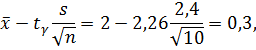
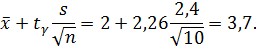
Таким образом,

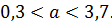
в) Доверительный интервал для генерального среднего квадратического отклонения а имеет вид:

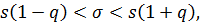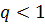
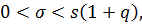если

если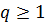

Соответствующие значения q указаны в таблице приложения 3. По заданным 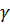= 0,95 и n = 10 находим q = 0,65. Теперь искомый доверительный интервал запишется следующим образом:

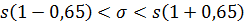
или

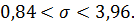
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ И ВЫБОРУ ВАРИАНТА

1. При выполнении контрольной работы студент должен руководствоваться следующими указаниями:

2. Работа должна выполняться в тетради (в клеточку) с полями, на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, специальность, номер группы, номер варианта.

3. Задачи располагаются в порядке номеров. Перед решением надо полностью переписать условие задачи.

4. Решение задач следует излагать подробно с указанием необходимых формул.

5. Задача геометрического содержания должна сопровождаться чертежом, выполненным аккуратно с указанием осей координат и единиц масштаба.

6. Контрольная работа должна выполняться самостоятельно. Если преподаватель установит несамостоятельность выполнения работы, то она не будет зачтена.

7. Студент должен исправить все недочеты и ошибки, указанные преподавателем в прорецензированной работе, после чего пройти собеседование по контрольной работе.

8. Вариант определяется по двум последним цифрам шифра по схеме:

1. По предпоследней цифре учебного шифра зачетной книжки выбирается номер строки;

2. По последней цифре учебного шифра зачетной книжки выбирается номер столбца;

3. На пересечении строки и столбца находится номер варианта.

9. Зачтенная контрольная работа является допуском студента к экзамену или зачету.

Для решения задач необходимо изучить следующие вопросы:

1) .Основные понятия и теоремы теории вероятностей.

2) Повторные независимые испытания. Формулы Бернулли, Муавра – Лапласа, Пуассона.

3) Случайные величины и их числовые характеристики.

4) Основные законы распределения.

5) Основные понятия математической статистики.

6) Понятие оценки параметров. Методы нахождения оценок.

Задание №1.

№№ 1-10.Три орудия производят по одному выстрелу в цель независимо друг от друга. Вероятность попадания в цель для каждого из них равны соответственно m, n, k. Найти вероятность того что:

а) в цель попадёт только одно орудие; б) в цель попадут только два орудия;

в) в цель попадёт хотя бы одно орудие.

1. n=0,7; m=0,9; k=0,8. 6. n=0,65; m=0,7; k=0,9.

2. n=0,6; m=0,9; k=0,9. 7. n=0,8; m=0,6; k=0,85.

3. n=0,8; m=0,8; k=0,7. 8. n=0,7; m=0,75; k=0,9.

4. n=0,75; m=0,6; k=0,8. 9. n=0,85; m=0,6; k=0,7.

5. n=0,9; m=0,7; k=0,75. 10. n=0,95; m=0,8; k=0,65.

№№ 11-20.Три студента участвуют независимо друг от друга в олимпиаде по математике. Вероятности победы для каждого из них равны соответственно m₁, m₂, m₃. Какова вероятность того, что:

а) победит только один студент; б) победу разделят два студента;

в) победит хотя бы один студент.

№№ 21-30. Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике, соответственно равны k₁, k₂, k₃. Найти вероятность того, что разыскиваемая формула содержится:

а) только в одном справочнике;

б) только в двух справочниках;

в) хотя бы в одном справочнике.

Задание №2.

№№ 1-10.Из урны, содержащей n белых и m красных шаров наугад вынимают два шара. Какова вероятность того, что:

а) оба шара красные; б) один шар белый, другой – красный;

в) хотя бы один шар белый.

№№ 11-20.В академической группе обучается n студентов, среди которых m девушек. На уборку территории выбирают произвольно трёх студентов. Какова вероятность того, что:

а) все три студента - юноши; б) два студента – юноши, один студент – девушка;

в) хотя бы один студент – юноша.

№№ 21-30.В коробке находиться n одинаковых изделий, причём m из них окрашены. Найти вероятность того, что среди двух извлечённых наугад изделий окажутся:

а) одно окрашенное изделие; б) два окрашенных изделия;

в) хотя бы одно окрашенное изделие.

Задание №3.

В вычислительной лаборатории имеются m автоматов и n полуавтоматов. Вероятность того, что за время выполнения некоторого расчёта автомат не выйдет из строя, равна p′; для полуавтомата эта же вероятность равна p″. Студент производит расчёт на удачу выбранной машине. Определить вероятность того, что до окончания расчёта выбранная машина не выйдет из строя.

Задание №4.

№№ 1 – 8. У рыбака есть три излюбленных места рыбалки. Эти места он посещает с одинаковой вероятностью. Вероятность того, что рыба клюнет в первом месте, близка к - р₁, во втором месте – р₂, в третьем месте – р₃. Известно, что рыбак забросил удочку один раз. Какова вероятность, что он поймал рыбу в первом из излюбленных мест?

1. р₁ = 0,13; р₂ = 0,14; р₃ = 0,12

2. р₁ = 0,23; р₂ = 0,12; р₃ = 0,13

3. р₁ = 0,12; р₂ = 0,14; р₃ = 0,34

4. р₁ = 0,15; р₂ = 0,13; р₃ = 0,23

5. р₁ = 0,14; р₂ = 0,34; р₃ = 0,25

6. р₁ = 0,35; р₂ = 0,13; р₃ = 0,12

7. р₁ = 0,45; р₂ = 0,23; р₃ = 0,15

8. р₁ = 0,13; р₂ = 0,23; р₃ = 0,25

№№ 9 – 16. Студент может купить билет в одной из трёх касс автовокзала. Вероятность того, что он направится к первой кассе, примерно равна – 0,12, ко второй – 0,13, к третей – 0,16. Вероятности того, что билетов уже нет в кассах, примерно такие: в первой кассе – р₁, во второй – р₂, в третей – р₃. Какова вероятность того, что он купил билет? Определить вероятность того, что он купил билет во второй кассе?

9. р₁ = 0,15; р₂= 0,16; р₃= 0,18.

10. р₁ = 0,25; р₂= 0,13; р₃= 0,14.

11. р₁ = 0,35; р₂= 0,12; р₃= 0,38.

12. р₁ = 0,45; р₂= 0,23; р₃= 0,17.

13. р₁ = 0,16; р₂= 0,25; р₃= 0,27.

14. р₁ = 0,14; р₂= 0,18; р₃= 0,35.

15. р₁ = 0,13; р₂= 0,16; р₃= 0,15.

16. р₁ = 0,12; р₂= 0,13; р₃= 0,14.

№№ 17 – 24 Семена для посева в хозяйство поступают из трёх семеноводческих хозяйств. Причём первое и второе хозяйство присылают по 40 % всех семян. Всхожесть семян из первого хозяйства – р₁, второго – р₂, третьего – р₃.

1) Определить вероятность того, что наудачу взятое семя не взойдёт.

2) На удачу взятое семя не взошло. Какова вероятность, что оно получено от второго хозяйства?

17. р₁ = 90%; р₂ = 85%; р₃ = 95%

18. р₁ = 80%; р₂ = 93%; р₃ = 82%

19. р₁ = 78%; р₂ = 94%; р₃ = 85%

20. р₁ = 87%; р₂ = 89%; р₃ = 79%

21. р₁ = 91%; р₂ = 93%; р₃ = 86%

22. р₁ = 92%; р₂ = 88%; р₃ = 77%

23. р₁ = 97%; р₂ = 83%; р₃ = 88%

24. р₁ = 90%; р₂ = 81%; р₃ = 84%

№№ 25 – 30. Покупатель с равной вероятностью посещает каждый из трёх магазинов. Вероятность того, что покупатель приобретёт товар в первом магазине равна – р₁, втором – р₂, в третьем – р₃. Определить вероятность того, что покупатель приобретёт товар в каком – либо магазине. Покупатель приобрёл товар. Найти вероятность того, что он купил его во втором магазине?

25. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

26. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

27. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

28. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

29. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

30. р₁ = 0,4; р₂ = 0,6; р₃ = 0,8

Задание №5.

№№ 1-10.Всхожесть семян данного растения составляет p%. Какова вероятность того, что из n посеянных семян взойдут:

а) m семян;

б) не менее m семян.

№№ 11-20. В водоёме лососи составляют q%. Найти вероятность того, что из n пойманных в этом водоёме рыб окажется:

а) m лососей;

б) не более m лососей.

№№ 21-30. В партии деталей число бракованных составляет p%. Какова вероятность того, что среди взятых наудачу n деталей не бракованные окажутся:

а) m деталей;

б) менее m деталей.

Задание №6.

№№ 1-6.Вероятность поражения цели при каждом выстреле равна p. Найти наивероятнейшее число попаданий в серии из n выстрелов и вычислить вероятность соответствующего события.

1. p=0,2 n=5

2. p=0,3 n=6

3. p=0,35 n=4

4. p=0,25 n=7

5. p=0,4 n=3

6. p=0.15 n=8

№№ 7-12.Всхожесть семян растения данного сорта составляет m%. Посеяли n семян. Найти наивероятнейшее число всходов и вычислить вероятность соответствующего события.

7. m=90 n=8

8. m=80 n=5

9. m=95 n=6

10. m=85 n=7

11. m=70 n=4

12. m=75 n=9

№№ 13-24.На склад поступило n ящиков, содержащих стеклянные изделия. Вероятность того, что в любом ящике окажется битое изделие, равна p. Найти наивероятнейшее число ящиков, содержащих неповреждённые изделия и вычислить соответствующего события.

13,19. p=0,75 n=8

14,20. p=0,4 n=6

15,21. p=0,55 n=7

16,22. p=0,6 n=9

17,23. p=0,7 n=10

18,24. p=0,65 n=11

№№ 25-30.Вероятность того, что любой из лотерейных билетов окажется выигрышным, равна p. Приобретено n билетов. Найти наивероятнейшее число выигрышных среди них, и вычислить вероятность соответствующего события.

25. p=0,3 n=6

26. p=0,45 n=7

27. p=0,55 n=8

28. p=0,4 n=10

29. p=0,5 n=9

30. p=0,35 n=11

Задание №7.

№№ 1-10.Баскетболист забрасывает штрафной примерно с вероятностью p. Какова вероятность того, что среди n бросков будут удачными:

а) все броски;

б) не менее k₁ и не более k₂ бросков.

1. n=20 p=0,8 k₁=15 k₂=18

2. n=18 p=0,7 k₁=10 k₂=15

3. n=12 p=0,85 k₁=8 k₂=12

4. n=20 p=0,6 k₁=16 k₂=19

5. n=18 p=0,9 k₁=14 k₂=18

6. n=19 p=0,8 k₁=13 k₂=16

7. n=16 p=0,75 k₁=11 k₂=15

8. n=20 p=0.3 k₁=4 k₂=10

9. n=15 p=0,5 k₁=5 k₂=9

10. n=19 p=0,45 k₁=7 k₂=11

№№ 11-20.Вероятность рождения девочки равна p. Чему равна вероятность того, что среди n новорождённых:

а) все девочки;

б) не менее k₁ и не более k₂ девочек.

11. n=30 p=0,485 k₁=13 k₂=18

12. n=32 p=0,48 k₁=10 k₂=20

13. n=29 p=0,49 k₁=10 k₂=18

14. n=26 p=0,495 k₁=8 k₂=14

15. n=31 p=0,475 k₁=12 k₂=16

16. n=33 p=0,47 k₁=13 k₂=17

17. n=34 p=0,46 k₁=12 k₂=19

18. n=35 p=0,465 k₁=14 k₂=20

19. n=36 p=0,45 k₁=12 k₂=17

20. n=33 p=0,455 k₁=13 k₂=16

№№ 21-30.Вероятность того, что саженец ели прижился, и будет расти примерно равна p. Посажено n саженцев ели. Какова вероятность того, что нормально вырастут:

а) все посаженные ели;

б) не менее k₁ и не более k₂ елей.

21. n=400 p=0,8 k₁=300 k₂=340

22. n=420 p=0,75 k₁=310 k₂=320

23. n=350 p=0,9 k₁=300 k₂=330

24. n=300 p=0,85 k₁=240 k₂=270

25. n=320 p=0,95 k₁=290 k₂=318

26. n=450 p=0,7 k₁=290 k₂=330

27. n=500 p=0,65 k₁=315 k₂=335

28. n=440 p=0,55 k₁=222 k₂=262

29. n=480 p=0,5 k₁=220 k₂=260

30. n=380 p=0,6 k₁=200 k₂=256

Задание №8.

Две независимые дискретные случайные величины X и Y заданы своими законами распределения. Найти математическое ожидание и дисперсию для случайной величины W=2X – 3Y

1. X -3 -7 1 2 Y 2 4

Y 0,1 0,2 0,2 0,5 P 0,7 0,3

2. X -3 2 6 4 Y 3 6

Y 0,3 0,3 0,2 0,2 P 0,8 0,2

3. X -5 1 2 4 Y 2 4

Y 0,2 0,3 0,1 0,4 P 0,6 0,4

4. X -4 0 2 5 Y 3 5

Y 0,1 0,5 0,2 0,2 P 0,2 0,8

5. X -2 -1 3 7 Y 1 6

Y 0,1 0,3 0,3 0,3 P 0,3 0,7

6. X -3 -1 0 2 Y 0 4

Y 0,2 0,3 0,4 0,1 P 0,9 0,1

7. X -5 -2 3 2 Y 1 7

Y 0,1 0,6 0,1 0,2 P 0,4 0,6

8. X -4 -1 3 8 Y 2 3

Y 0,1 0,3 0,5 0,1 P 0,7 0,3

9. X -7 0 1 2 Y -4 4

Y 0,5 0,1 0,1 0,3 P 0,3 0,7

10. X -2 -1 0 1 Y -3 4

Y 0,4 0,4 0,1 0,1 P 0,2 0,8

11. X -8 -6 -1 5 Y -2 1

Y 0,6 0,1 0,2 0,1 P 0,8 0,2

12. X -7 -4 0 3 Y -4 3

Y 0,3 0,3 0,1 0,3 P 0,1 0,9

13. X -2 0 1 4 Y -6 3

Y 0,3 0,2 0,3 0,2 P 0,4 0,6

14. X -6 -3 -2 3 Y -8 2

Y 0,1 0,2 0,4 0,3 P 0,7 0,3

15. X -5 -4 -2 2 Y -3 3

Y 0,1 0,3 0,4 0,2 P 0,6 0,4

16. X -2 -1 3 4 Y -4 0

Y 0,2 0,2 0,2 0,4 P 0,9 0,1

17. X -3 3 4 6 Y 0 3

Y 0,1 0,2 0,3 0,4 P 0,2 0,8

18. X -6 -2 1 2 Y -1 3

Y 0,3 0,3 0,2 0,2 P 0,7 0,3

19. X -2 -1 1 2 Y 1 3

Y 0,6 0,1 0,1 0,2 P 0,4 0,6

20. X -4 -3 0 4 Y -2 3

Y 0,3 0,5 0,1 0,1 P 0,5 0,5

21. X -6 -5 3 4 Y 0 3

Y 0,2 0,2 0,2 0,4 P 0,4 0,6

22. X -7 -2 2 7 Y -3 0

Y 0,2 0,4 0,1 0,3 P 0,5 0,5

23. X -3 -2 3 4 Y -4 1

Y 0,3 0,4 0,1 0,2 P 0,6 0,4

24. X -7 0 1 3 Y -1 1

Y 0,3 0,2 0,3 0,2 P 0,4 0,6

25. X -4 -3 0 4 Y 0 3

Y 0,5 0,3 0,1 0,1 P 0,9 0,3

26. X -5 -2 2 6 Y -3 1

Y 0,3 0,2 0,4 0,1 P 0,5 0,5

27. X -9 0 1 2 Y -3 0

Y 0,7 0,1 0,1 0,1 P 0,7 0,3

28. X -6 -5 -4 2 Y -1 4

Y 0,2 0,6 0,1 0,1 P 0,2 0,8

29. X -1 0 3 4 Y -1 7

Y 0,3 0,1 0,3 0,3 P 0,9 0,1

30. X -4 -3 -2 8 Y -4 2

Y 0,5 0,1 0,2 0,2 P 0,3 0,7

Задание №9

В задачах 1 – 30 задана выборка значений нормально распределённого признака X (даны значения признака x_i и соответствующие им частоты n_i). Найти: а) выборочную среднюю x и исправленное среднее квадратическое отклонение s; б) доверительный интервал, покрывающий неизвестное математическое ожидание a признака X; в) доверительный интервал, покрывающий неизвестное среднее квадратическое отклонение g признака X (надёжность оценки во всех вариантах считать равной y=0,95).

1. x_i -3 1 2 4 5 7

n_i 1 2 2 3 2 4

2. x_i -5 -2 3 4 6 7

n_i 2 3 1 3 4 5

3. x_i -3 -2 1 2 4 6

n_i 3 2 2 4 5 1

4. x_i -5 -4 2 4 7 8

n_i 1 2 4 5 4 3

5. x_i -6 -4 -3 2 3 5

n_i 2 4 6 1 3 5

6. x_i -2 -1 1 3 5 6

n_i 1 2 4 6 3 1

7. x_i -7 -6 -4 2 3 5

n_i 1 3 5 3 4 2

8. x_i -3 -2 1 4 5 7

n_i 2 4 6 1 3 3

9. x_i -5 -2 -1 2 4 6

n_i 1 4 6 5 1 3

10. x_i -6 -2 -1 3 5 7

n_i 1 2 4 4 5 1

11. x_i -3 1 4 5 7 8

n_i 4 2 3 5 1 1

12. x_i -3 -2 1 3 4 7

n_i 1 4 4 3 5 1

13. x_i -3 -1 3 4 5 6

n_i 2 4 5 4 3 2

14. x_i -5 -4 1 3 6 8

n_i 2 3 3 4 3 1

15. x_i 2 4 5 7 8 9

n_i 1 4 3 3 4 1

16. x_i -2 -1 1 3 5 6

n_i 2 2 3 1 4 5

17. x_i -1 2 3 5 7 9

n_i 2 3 5 5 1 1

18. x_i -5 -4 6 7 8 9

n_i 3 3 1 4 2 2

19. x_i -4 -2 -1 3 5 6

n_i 1 5 5 4 3 1

20. x_i -2 -1 2 4 5 7

n_i 1 5 5 1 3 3

21. x_i -4 -2 -1 2 3 7

n_i 1 4 4 3 1 2

22. x_i -5 -3 -1 2 4 7

n_i 2 1 1 4 3 2

23. x_i -3 -2 1 3 5 8

n_i 1 2 4 3 2 1

24. x_i -4 -3 2 3 4 6

n_i 2 4 3 5 2 2

25. x_i -3 -1 2 4 5 6

n_i 1 3 4 5 2 1

26. x_i -6 -3 -1 2 3 5

n_i 2 4 5 4 3 2

27. x_i -5 -4 2 4 7 8

n_i 1 3 3 5 4 2

28. x_i -3 -2 1 4 5 7

n_i 1 4 6 5 1 3

29. x_i -1 2 3 5 7 9

n_i 1 4 3 3 4 1

30. x_i -6 -4 -3 2 3 5

n_i 2 4 5 1 1 3

ПРИЛОЖЕНИЕ 1

ЧАСТЬ 1

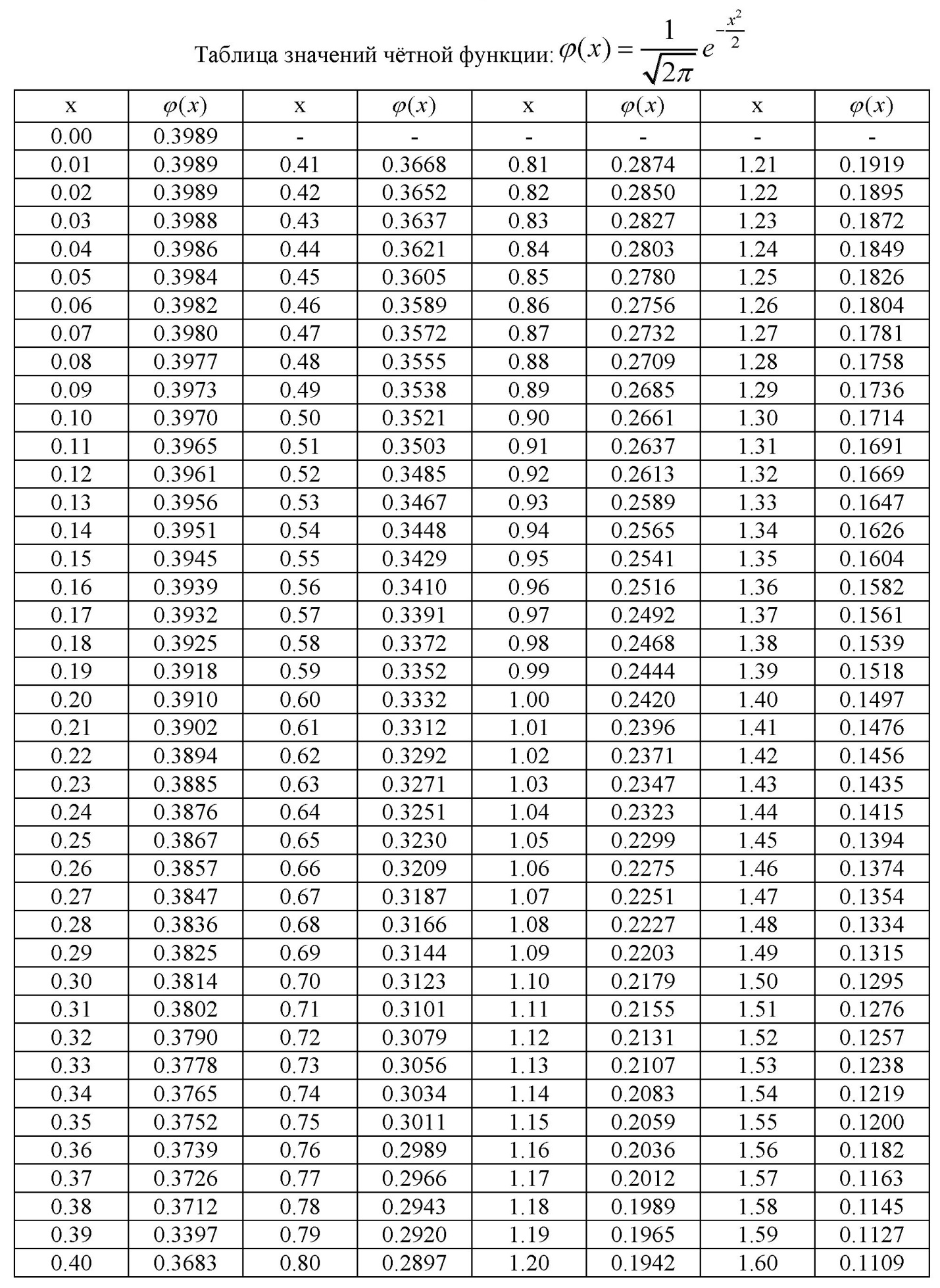
ПРИЛОЖЕНИЕ 1

ЧАСТЬ 2

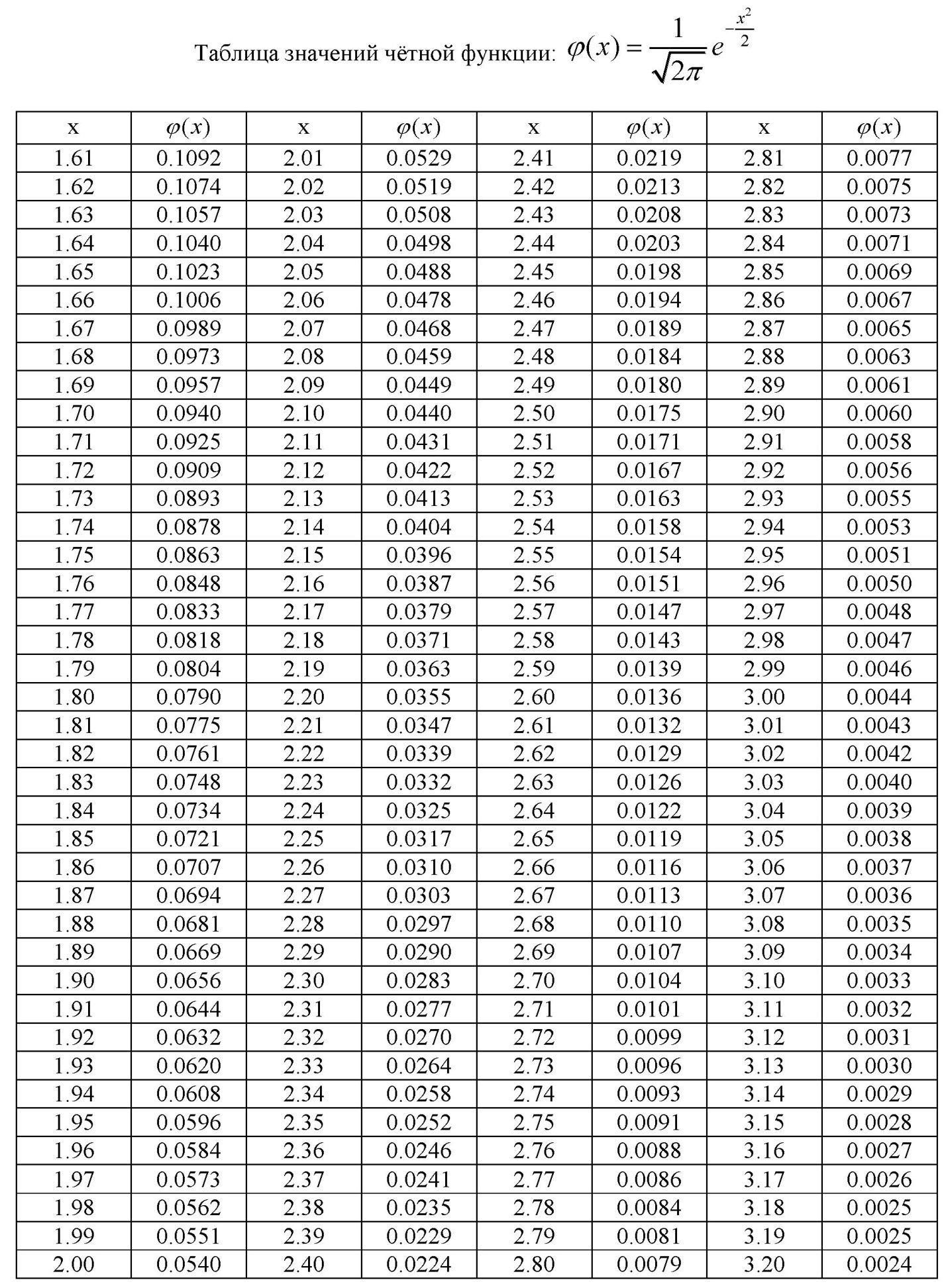
ПРИЛОЖЕНИЕ 1

ЧАСТЬ 3

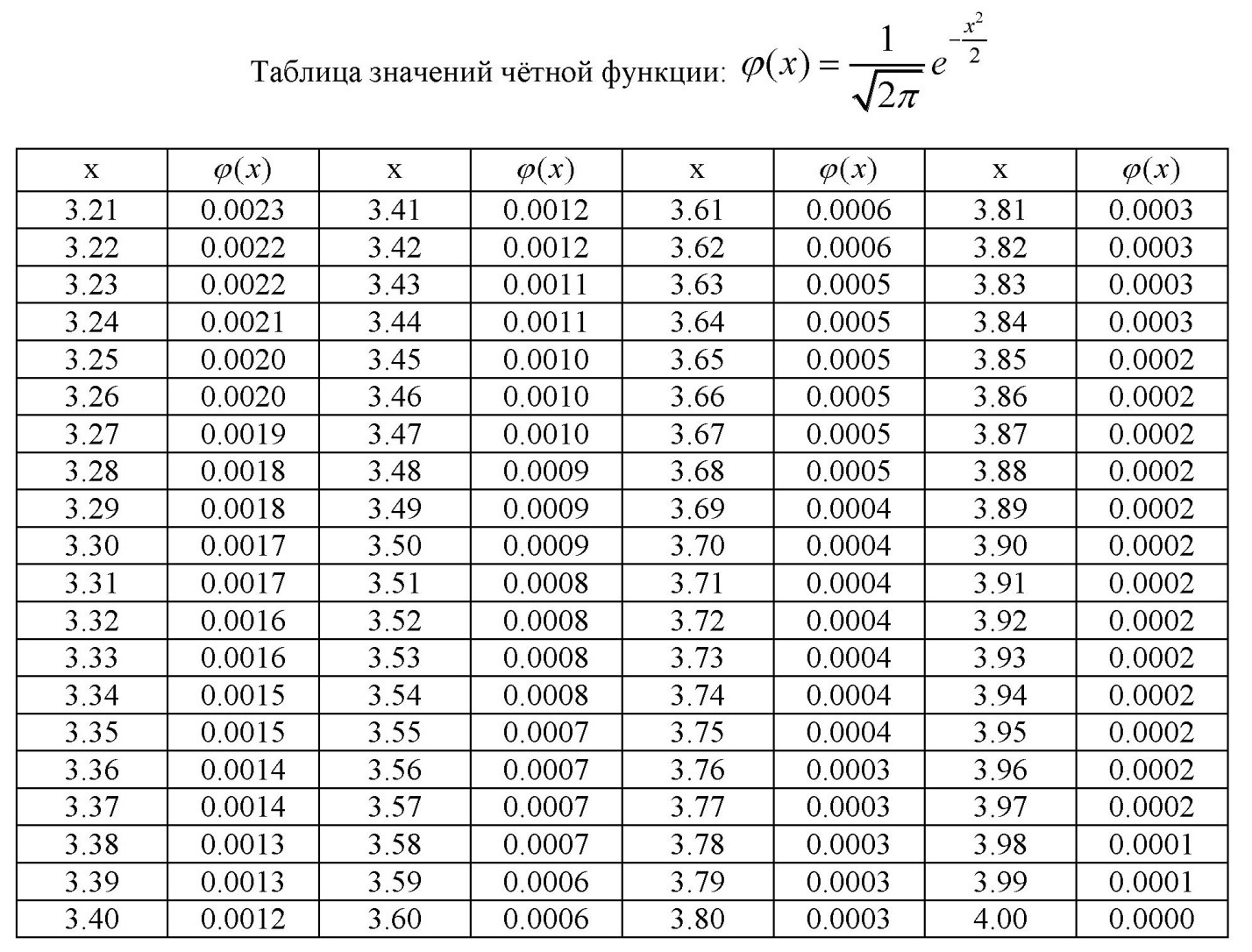
ПРИЛОЖЕНИЕ 2

ЧАСТЬ 1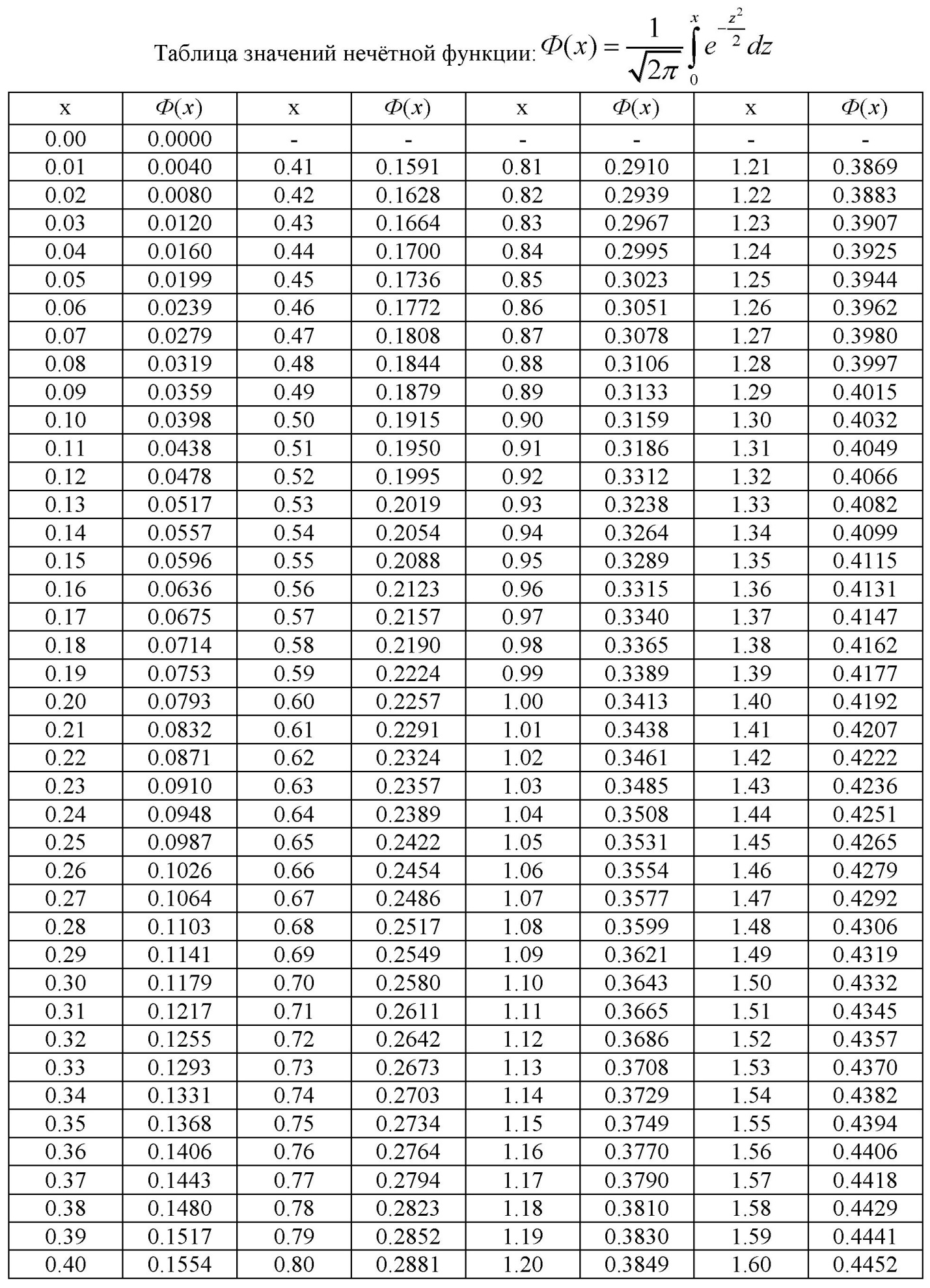

ПРИЛОЖЕНИЕ 2

ЧАСТЬ 2

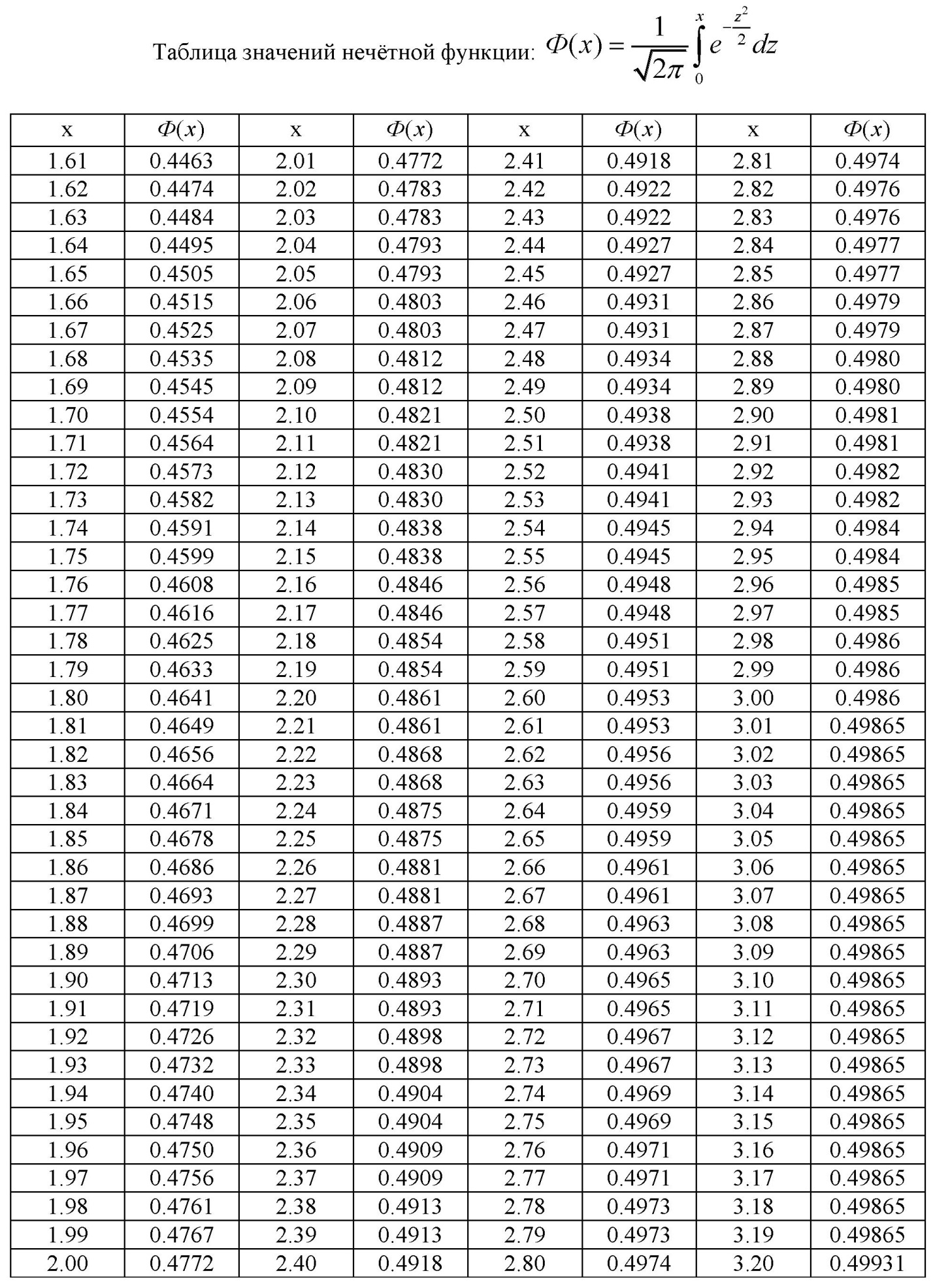
ПРИЛОЖЕНИЕ 2

ЧАСТЬ 3

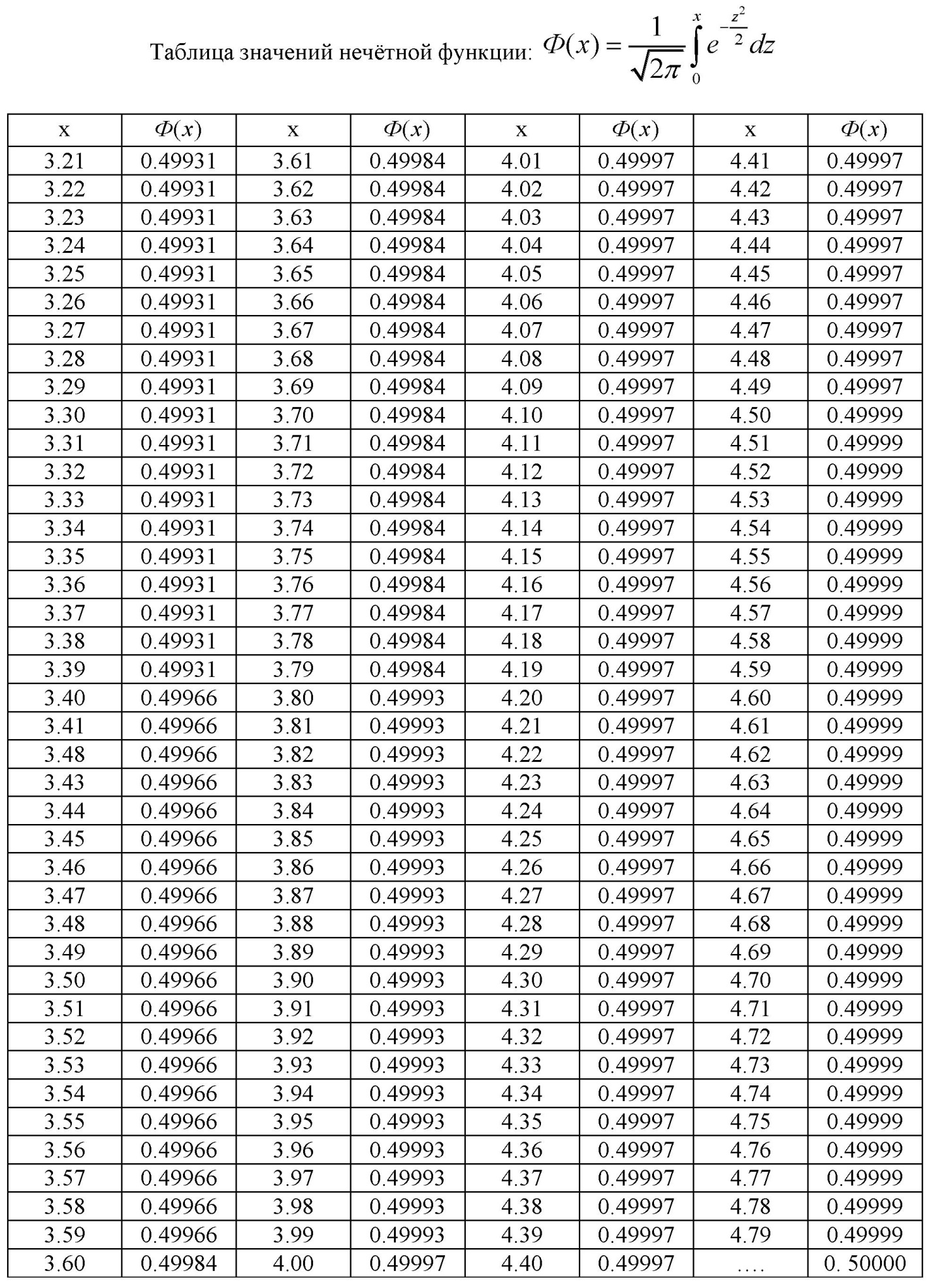
ПРИЛОЖЕНИЕ 3

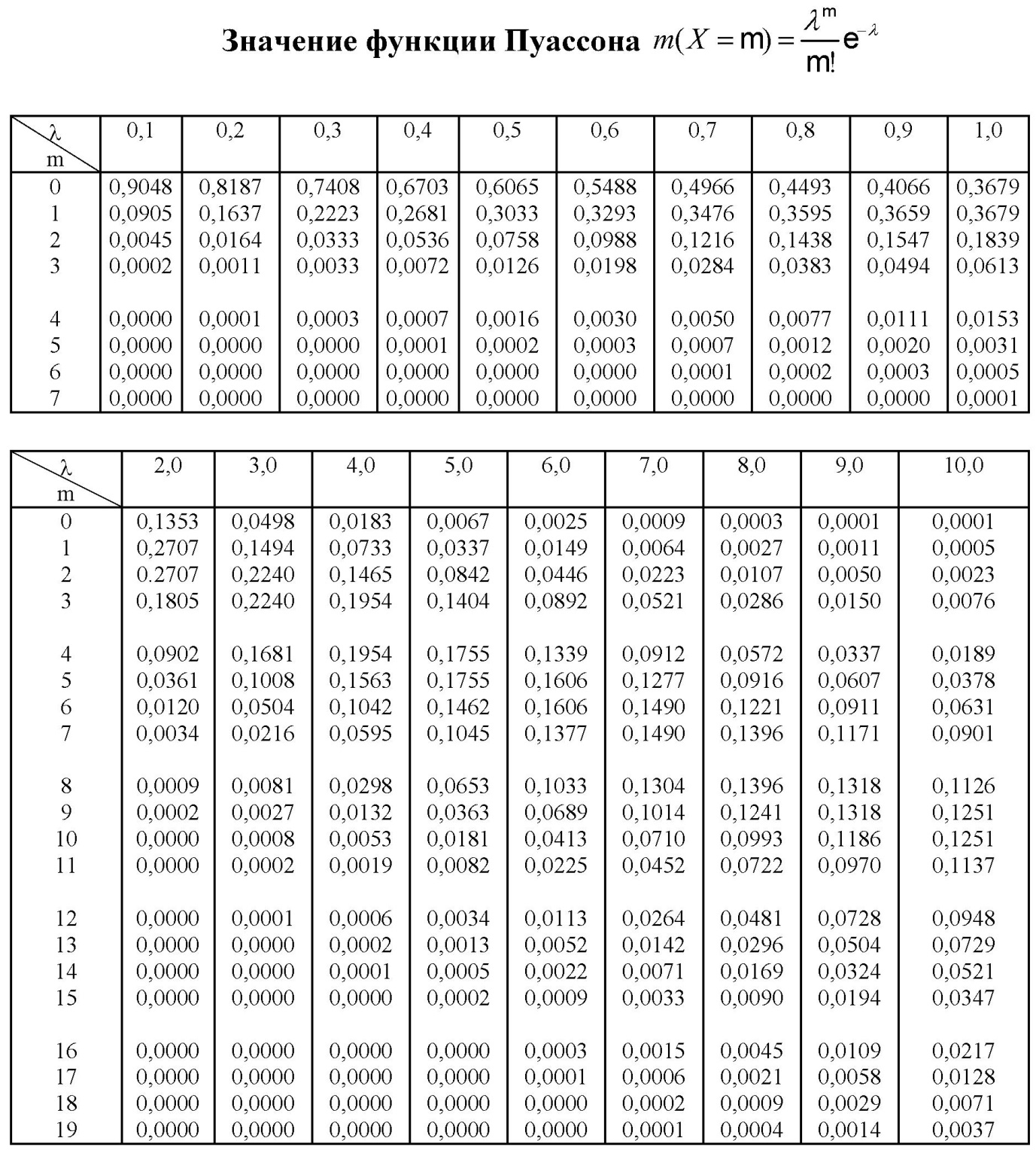
ПРИЛОЖЕНИЕ 4

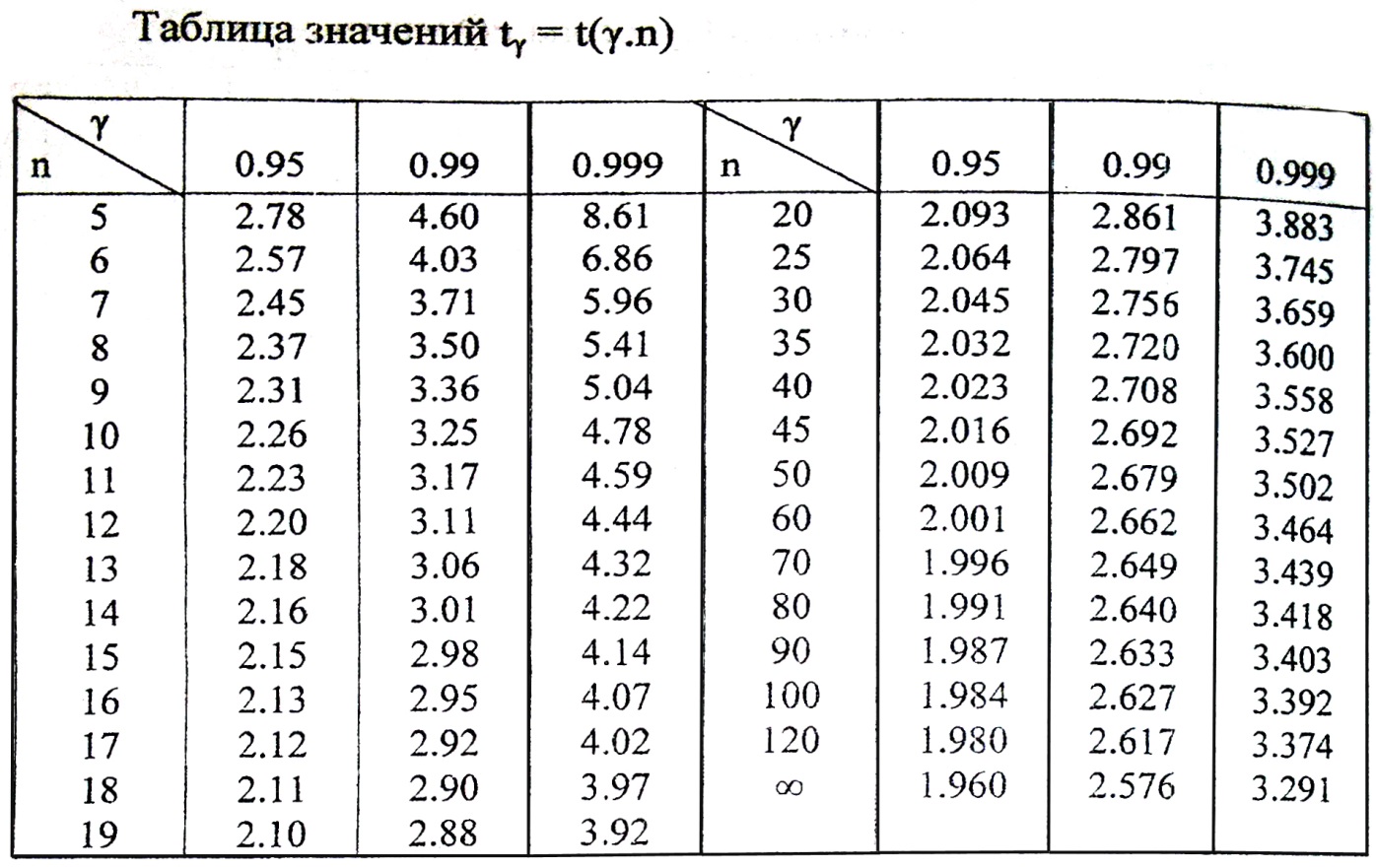
ПРИЛОЖЕНИЕ 5