Свойства степенных рядов

Рассмотрим степенной ряд 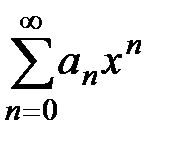, у которого интервал сходимости 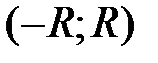, тогда сумма степенного ряда 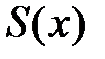определена для всех 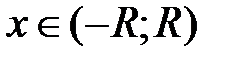и можно записать равенство .

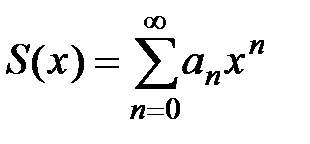Свойство 1. Степенной ряд 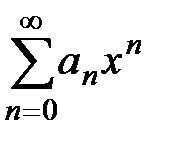сходится абсолютно в любом промежутке 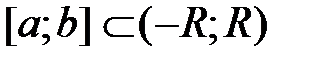, лежащем в интервале сходимости, причём сумма степенного ряда является непрерывной функцией при всех .

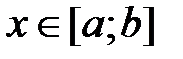Свойство 2. Если отрезок 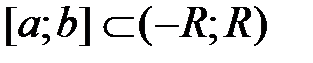, то степенной ряд можно
почленно интегрировать от a до b, т.е. если

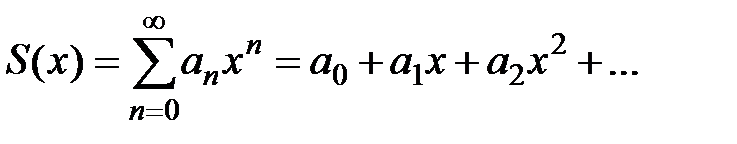, то

.
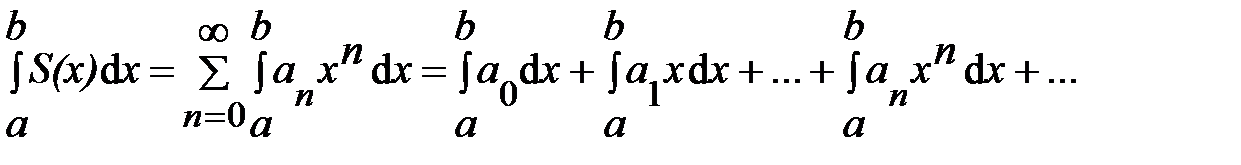При этом радиус сходимости не меняется:

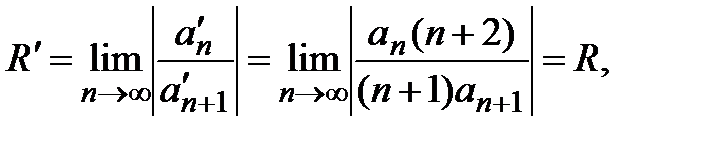
где 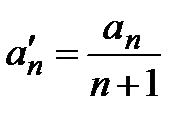− коэффициенты проинтегрированного ряда.

Свойство 3. Сумма степенного ряда есть функция, имеющая внутри интервала сходимости производные любого порядка. Производные от суммы степенного ряда будут суммами рядов, полученных из данного степенного ряда почленным дифференцированием соответствующее число раз, причём радиусы сходимости таких рядов будут те же, что и у исходного ряда.

Если ,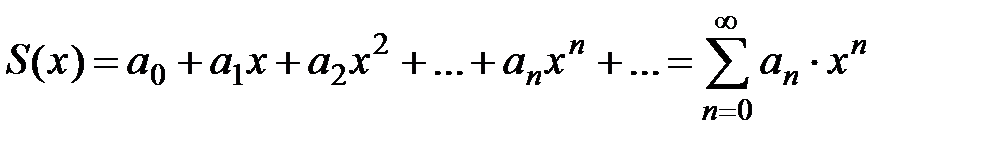
то ,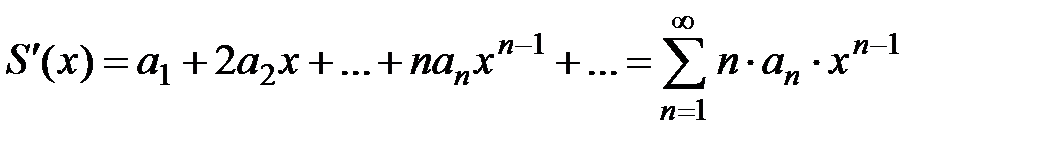
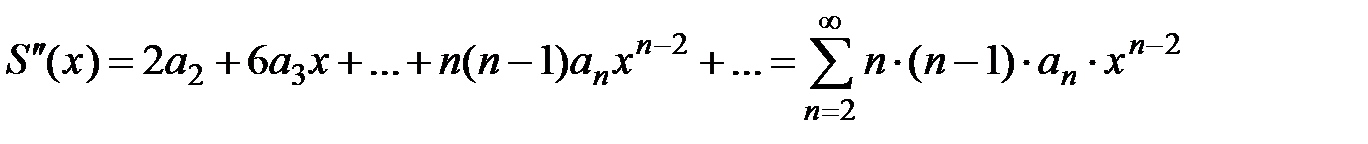, …, и т.д.

Формула Тейлора

Рассмотрим важную задачу, которая решается в теории функциональных рядов: по заданной функции найти сходящийся функциональный ряд того или иного типа, сумма которого в области сходимости равнялась бы заданной функции. Такая задача называется разложением функции в ряд, например, степенной.

Пусть функция 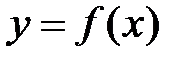определена в некоторой окрестности точки

х₀: 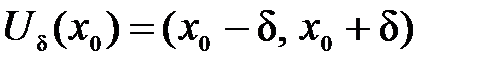, где 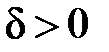, причём в этой окрестности функция имеет все производные до 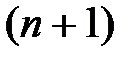-го порядка.

Задача: Подберём многочлен n-й степени

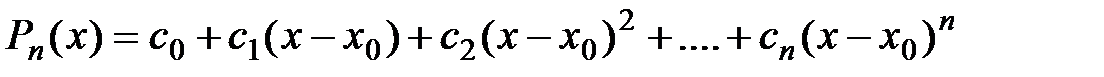по степеням 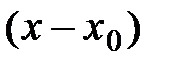так, чтобы в точке х₀ совпадали значения 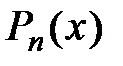и 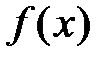, а также значения их производных до ( 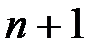)-го порядка включительно. Тогда считаем, что в окрестности точки х₀ такой многочлен 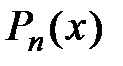будет приближать данную функцию с некоторой точностью.

Коэффициенты многочлена 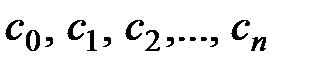являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий:

, , , … , .

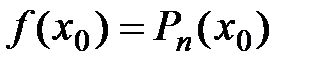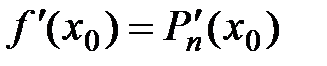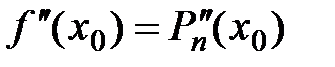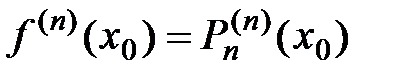Для нахождения этих коэффициентов найдём производные до n-го порядка от :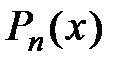

,

,

…

,

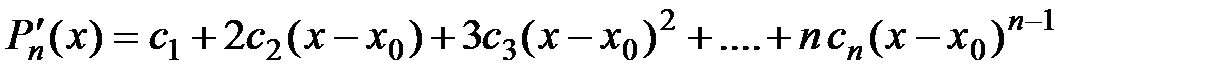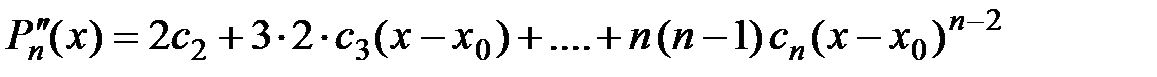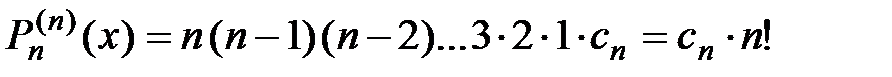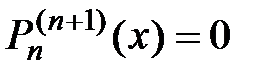, при всех 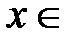R.

Подставим в эти соотношения 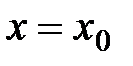и приравняем 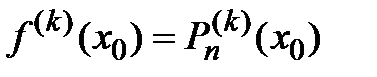, где :

, , ,

, … .

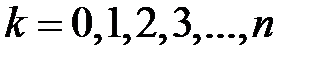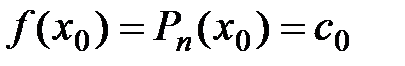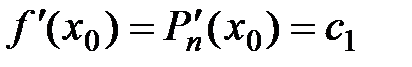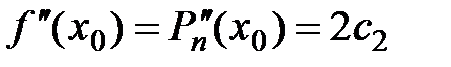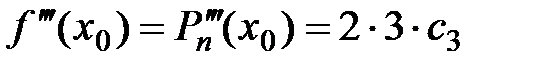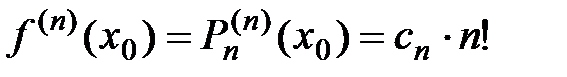Находим выражения для 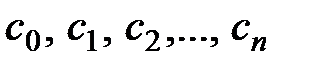, решая полученную систему уравнений:

.

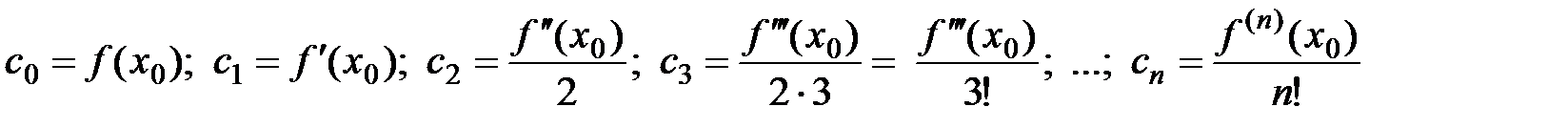Получаем общую формулу для определения коэффициентов многочлена :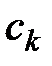

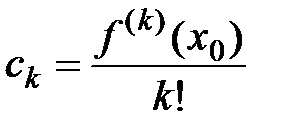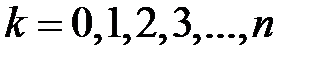, . (4)

Тогда многочлен примет следующий вид: .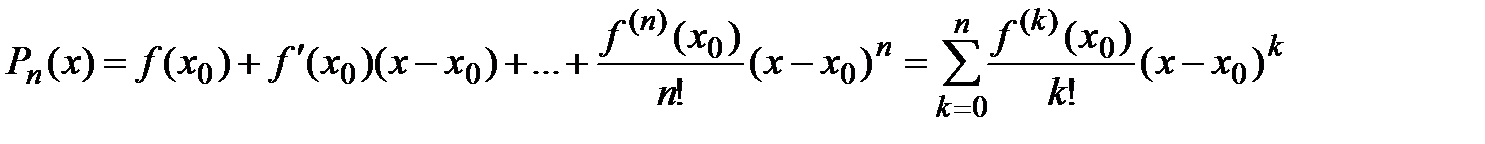
Этот многочлен называется многочленом Тейлора для функции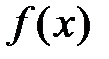

по степеням 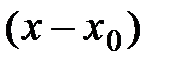, где 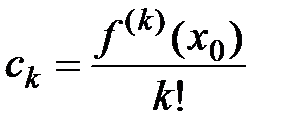называются коэффициентами многочлена Тейлора, .

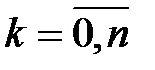Таким образом, для каждой функции 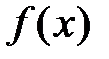, удовлетворяющей поставленным условиям при 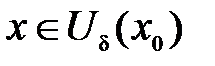, можно найти многочлен Тейлора 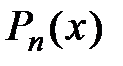(в точке х₀ функция 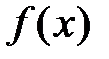и многочлен 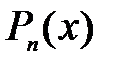совпадают со своими производными до n-го порядка).

Разность 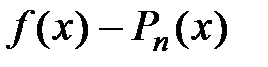, обозначенную через 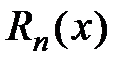, называют остаточным членом формулы Тейлора, которая имеет вид:

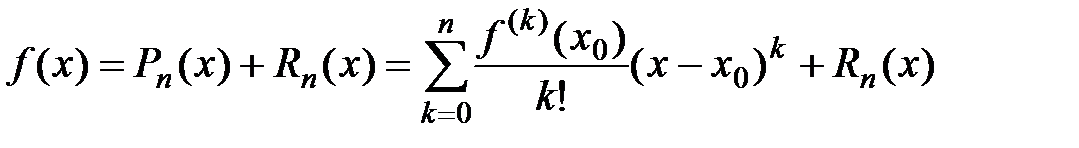(5)

Формула (5) называется формулой Тейлора для функции 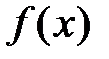по степеням 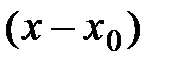порядка n. Отметим, что

.

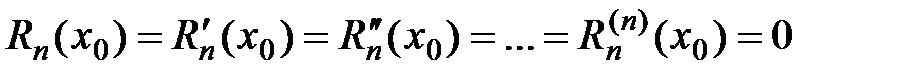Величина остаточного члена формулы Тейлора 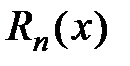играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов.

1) Остаточный член в форме Пеано. Преобразуем остаточный член формулы Тейлора, используя некоторые понятия из теории пределов.

а) Функция 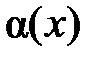называется бесконечно малой при 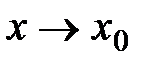, если .

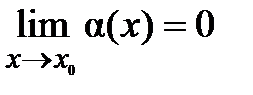б) Бесконечно малая функция 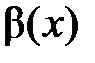называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции 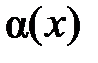при 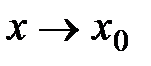, если существует 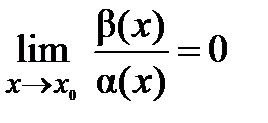и записывается следующим образом: 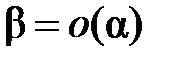(что читается так: «β есть о малое от α).

Рассмотрим формулу Тейлора для функции 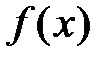по степеням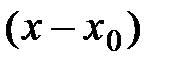
порядка n: 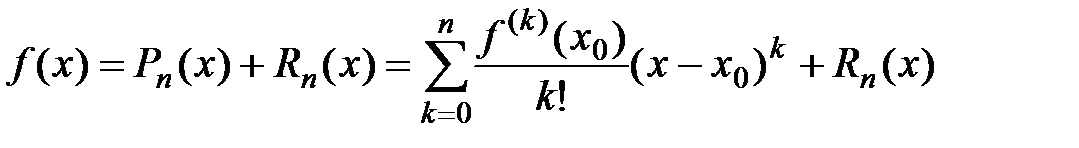. Остаточный член в формуле Тейлора имеет вид: 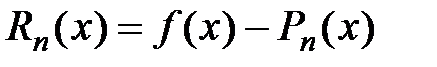. Из построения многочлена Тейлора следует 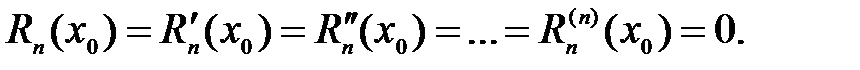Тогда 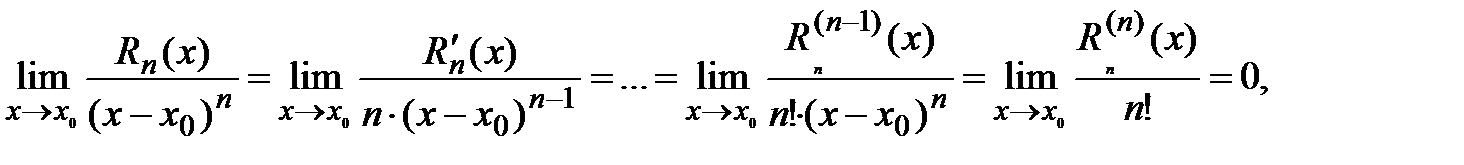откуда остаточный член формулы Тейлора можно записать в виде: 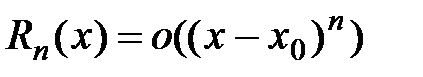, т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно 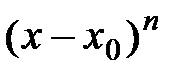при .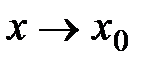

Формула Тейлора 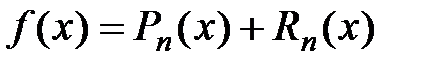, в которой ,
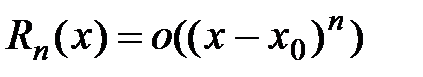называется формулой Тейлора с остаточным членов в форме Пеано. Поскольку остаточный член при 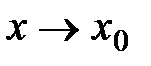является бесконечно малой величиной, то можно считать, что разность 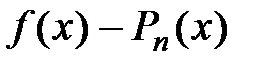бесконечно мала, т.е. .

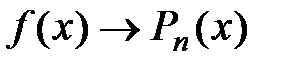2) Остаточный член в форме Лагранжа. Запишем остаточный член в виде

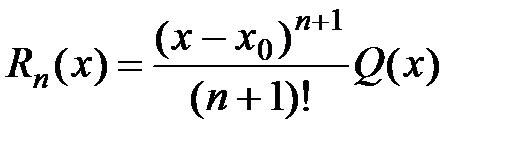, где Q(x) есть некоторая функция, подлежащая определению. Можно доказать, что 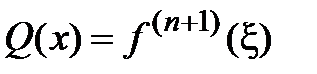, где точка ξ заключена между х и х₀: 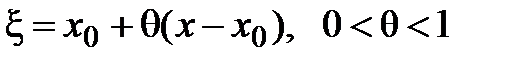, т.е. остаточный член имеет вид: 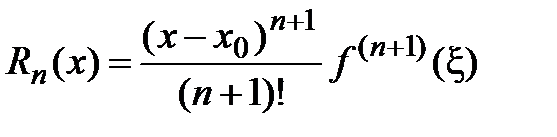. Тогда формула Тейлора примет вид 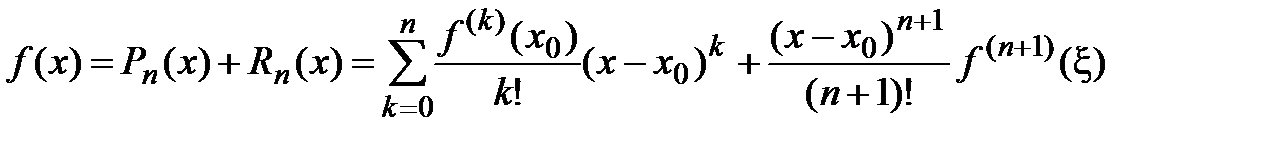, который называется формулой Тейлора с остаточным членом в форме Лагранжа.

Рассмотрим частные случаи формулы Тейлора.

– Если в формуле Тейлора с остаточным членом в форме Лагранжа положить 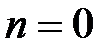, то получаем формулу конечного приращения: 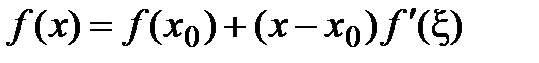(теорема Лагранжа).

– Если в формуле Тейлора положить 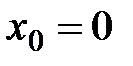, то получим формулу, которую называют формулой Маклорена:

,

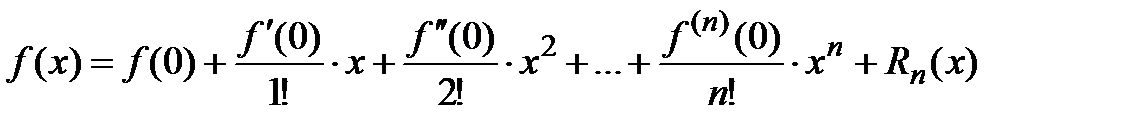где остаточный член можно записать в форме Пеано: 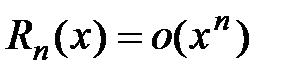или в форме Лагранжа:

.

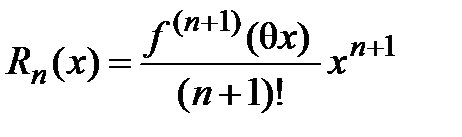Формула Маклорена является разложением функции 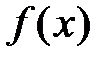в виде многочлена по степеням х.

Пример 5. Разложить функцию 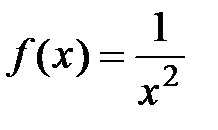в виде многочлена третьего

порядка по степеням 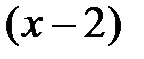с остаточным членом в форме Лагранжа.

Решение. Запишем формулу Тейлора для функции 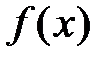в точке 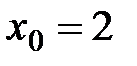в

виде многочлена 3-го порядка с остаточным членом в форме Лагранжа

,

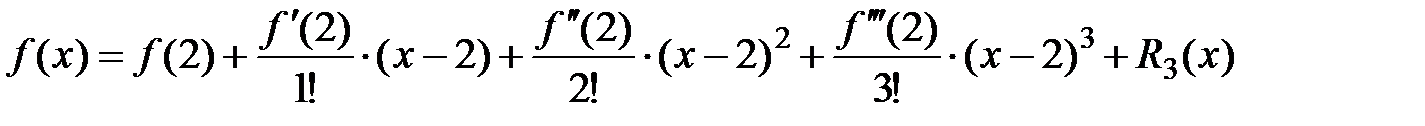где .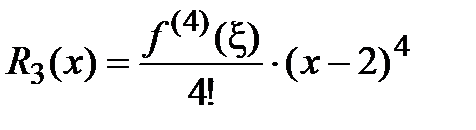

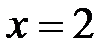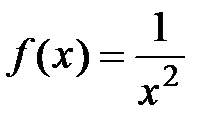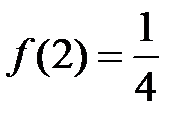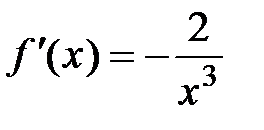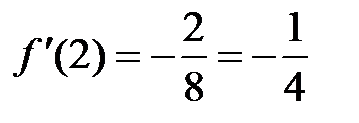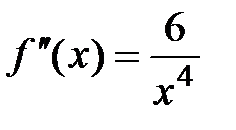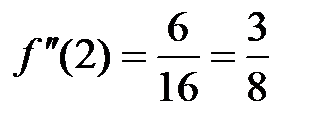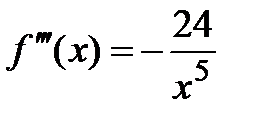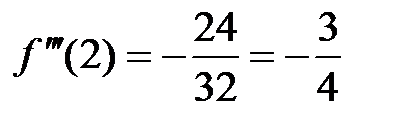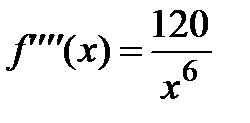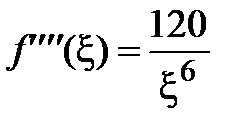Находим производные нужного порядка в точке :

, ; , ;
, ; , ; , , где .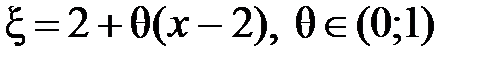

Полученные данные подставляем в формулу Тейлора 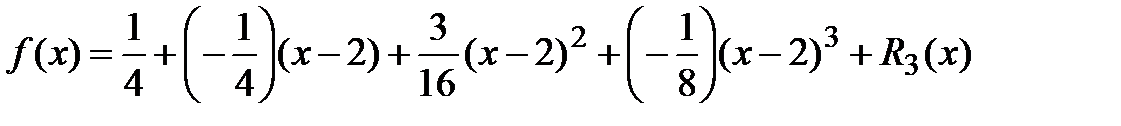и вычисляем .

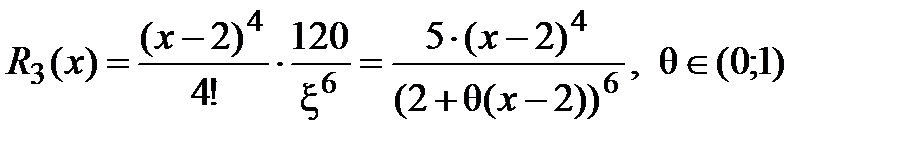Можно сказать, что функция 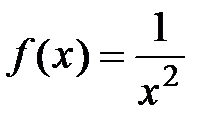заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора 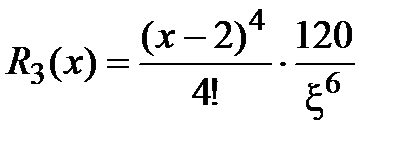при 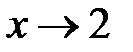.