Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 82 + 0 * 81 + 0 * 80 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
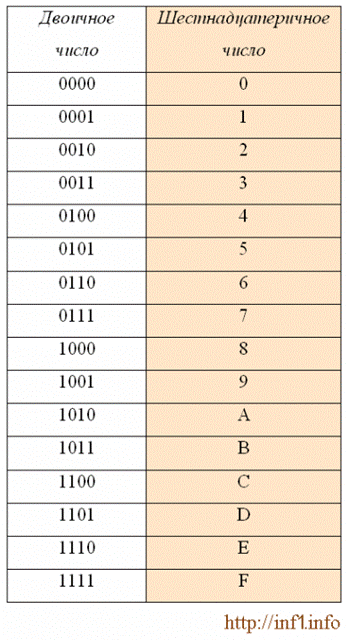
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи - это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние.
Системы счисления. Перевод чисел
В десятичную систему счисления
Из двоичной
101,012 = = 1 * 22 + 0 * 21 + 1 * 20 + 0 * 2-1 + 1 * 2-2 = = 4 + 0 + 1 + 0 + 1/4 = = 5,2510Из восьмеричной
253,318 = = 2 * 82 + 5 * 81 + 3 * 80 + 3 * 8-1 + 1 * 8-2 = = 128 + 40 + 3 + 3/8 + 1/64 = = 171 + 0,375 + 0,015625 = = 171,39062510Из шестнадцатеричной
42D16 == 4 * 162 + 2 * 161 + 13 * 160 == 1024 + 32 + 13 == 106910Из десятичной системы счисления
При переводе целых чисел из десятичной системы счисления последовательно выполняют деление этого числа и получаемых целых частных на основание выбранной системы счисления. Деление выполняют до тех пор, пока частное не будет равно нулю.
Число получают путем «сбора» остатков, начиная с конца.
В двоичную
34 / 2 = 17 (0)17 / 2 = 8 (1)8 / 2 = 4 (0)4 / 2 = 2 (0)2 / 2 = 1 (0)1 / 2 = 0 (1)3410 = 1000102
В восьмеричную
472 / 8 = 59 (0)59 / 8 = 7 (3)7 / 8 = 0 (7)47210 = 7308
В шестнадцатеричную
924 / 16 = 57 (12)57 / 16 = 3 (9)3 / 16 = 0 (3)92410 = 39C16
Перевод десятичных дробей из десятичной системы счисления
Дробь в десятичной системе счисления последовательно умножают на основание выбранной системы счисления пока не получиться нулевая дробная часть или достигнута требуемая точность. При каждом последующем умножении целая часть отбрасывается. Целые части результатов и составляют новую дробь. Записываются по порядку.
В двоичную дробь
0,225 * 2 = 0,450,45 * 2 = 0,90,9 * 2 = 1,80,8 * 2 = 1,60,6 * 2 = 1,20,2 * 2 = 0,40,4 * 2 = 0,80,8 * 2 = 1,6…0,22510 = 0,00111001…2
В восьмеричную дробь
0,225 * 8 = 1,80,8 * 8 = 6,40,4 * 8 = 3,20,2 * 8 = 1,60,6 * 8 = 4,8…0,22510 = 0,16314…8
В шестнадцатеричную дробь
0,225 * 16 = 3,60,6 * 16 = 9,60,6 * 16 = 9,6…0,22510 = 0,699…16
Арифметические операции в двоичной системе счисления
В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).
Сложение
Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
0 + 0 = 01 + 0 = 10 + 1 = 11 + 1 = 10В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально).
Сложим для примера два любых двоичных числа:
1101+ 101 ------ 10010Вычитание
Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
0 - 0 = 01 - 0 = 10 - 1 = (заем из старшего разряда) 11 - 1 = 0Пример:
1110- 101 ---- 1001Умножение
Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
0 * 0 = 01 * 0 = 00 * 1 = 01 * 1 = 1Пример:
1110* 10------+ 0000 1110 ------ 11100Деление
Деление выполняется так же как в десятичной системе счисления:
1110 | 10 |----10 | 111---- 11 10---- 10 10---- 0