Отношения между понятиями

Отношения между понятиями тесно связаны с отношениями между их объемами, т.е. множествами.

Условимся понятия обозначать строчными буквами латинского алфавита: а, b, с,…,z.

Пусть заданы два понятия а и b. Объемы их обозначим соответственно A и В.

Если объемы понятий а и b не пересекаются, т.е. если 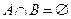, то говорят, что понятия а и bсовместимы.

Если объемы понятий а и b находятся в отношении пересечения, т.е. если 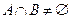, то говорят, что понятия aи bнесовместимы.

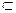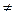Если объем понятия а является собственным подмножеством понятия b, т.е. если А В (А В), то говорят, что

1) понятие а является видовым по отношению к понятию b, а понятие b - родовым по отношению к понятию а.

2) понятие а уже понятия b, а понятие b шире понятия а.

3) понятие а есть частный случай понятия b, а понятие b, есть обобщение понятия а.

Например, если а - «прямоугольник», b - «четырехугольник», то их объемы А и В находятся в отношении включения 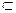(А В и А 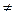В), поскольку всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» - видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» - родовое по отношению к понятию «прямоугольник».

Если объем понятия а равен объему понятия b, т.е. если А = В, то говорят, что понятия а и b тождественны.

Например, тождественны понятия «равносторонний треугольник» и «равноугольный треугольник», так как их объемы совпадают.

Пример. Установить отношения между следующими парами понятий a и b, если:

1) а - «прямоугольник», b - «ромб»; 2) а - «многоугольник», b - «параллелограмм»;

3) а - «прямая», b - «отрезок».

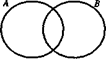
В случае 1) объемы понятий пересекаются, но не одно множество не является подмножеством другого. Следовательно, можно утверждать, что данные понятия а и b не находятся в отношении рода и вида.

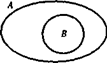
В случае 2) объемы данных понятий находятся в отношении включения, но не совпадают - всякий параллелограмм является многоугольником, но не наоборот. Следовательно, можно утверждать, что понятие «параллелограмм» - видовое по отношению к понятию «многоугольник», а понятие «многоугольник» - родовое по отношению к понятию «параллелограмм».

В случае 3) объемы понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком, Следовательно, данные понятия не находятся в отношении рода и вида.

О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок - часть прямой, а не ее вид. И если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как ее бесконечность.

Операции с понятиями

В процессе мышления с понятиями выполняют операции: обобщения, ограничения, определения и деления.

1. Обобщение понятия - это логическая операция, которая состоит в переходе от понятия с меньшим объемом (большим содержанием) к понятию с большим объемом (меньшим содержанием). Другими словами, обобщение понятия - это переход от видового понятия к родовому. При этом происходит расширение объема за счет отбрасывания существенных признаков.

Например, обобщая понятие "прямоугольник", можно перейти к понятию "четырехугольник", отбросив такое свойство, как "иметь все углы прямые".

2. Ограничение понятия - это логическая операция, которая состоит в переходе от понятия с большим объемом к понятию с меньшим объемом. Другими словами, ограничение понятия - это переход от родового понятия к видовому. При этом сужение объема происходит за счет расширения содержания.

Например, понятие "четырехугольник" можно ограничить, добавив к его содержанию свойство "иметь все прямые углы". В результате получим понятие "прямоугольник".

3. Определение понятия - это логическая операция, с помощью которой раскрывается содержание понятия, либо устанавливается значение термина.

Способы определения понятий различны.Прежде всего различают явные и неявные определения.

Неявные определения не имеют формы совпадения двух понятий. Примерами таких определений являются так называемые контекстуальные и остенсивные определения.

В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия. Посредством контекста устанавливается связь определяемого понятия с другими, известными, и тем, самым косвенно раскрывается его содержание. Примером контекстуального определения может быть определение уравнения и его решения, приведенное в учебнике математики, II класса (Моро М.И., Бантова М.А. Математика: Учеб. для 2 класса трехлетней начальной школы. - М.: Просвещение, 1987. - с. 196). Здесь после записи + 6 = 15 и перечня чисел 0, 5, 9, 10 идет текст: « К какому числу надо прибавить 6, чтобы, получилось 15? Обозначим неизвестное число латинской буквой х (икс):

х + 6= 15 - это уравнение.

Решить уравнение - значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9 + 6=15. Объясни, почему числа 0,5 и 10 не подходят».

Из приведенного текста следует, что уравнение - это равенство, в котором есть неизвестное число. Оно может быть обозначено буквой х и это число надо найти. Кроме того, из этого текста следует, что решение уравнения - это число, которое при подстановке вместо х обращает уравнение в верное равенство.

Остенсивные определения - это определения путем показа. Они используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают. Например, таким способом можно определить в начальной школе понятия равенства и неравенства:

2∙7>2∙6 78-9<78 37+6>37 9∙3=27 6∙4=4∙6 17-5=8+4

Это неравенства. Это равенства.

Остенсивные определения, как и контекстуальные, характеризуются некоторой незавершенностью. Действительно, определение посредством показа не выделяет числовые равенства (неравенства) из других предложений, в нем не указываются свойства, характерные для данных понятий. Они только связывают термины с определяемыми объектами. Поэтому после контекстуального или остенсивного определения понятия необходимо дальнейшее изучение свойств так определенных объектов.

Явные определенияимеют форму равенства, совпадения двух понятий.

Во всяком определении выделяют определяемое и определяющее понятия. Например, в предложении «Прямоугольником называется параллелограмм с прямым углом» определяемое понятие "прямоугольник"(т.е. что определяется), а определяющее понятие -"параллелограмм с прямым углом" (т.е. то, через что определяется данное понятие).

Если обозначить через а первое понятие, а через b - второе, то данное определение можно представить в таком виде:

а есть (по определению) b.

Слова «есть (по определению)» обычно заменяют символом 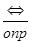, тогда определение выглядит так: a 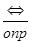b

Читают: «а равносильно b по определению». Можно прочитать эту запись еще и так: «а тогда и только тогда, когда b». Такова структура явных определений.

Среди явных определений в математике чаще всего используются определения через род и видовое отличие. Рассмотрим их подробнее.