Стохастической неопределенности
Принятие решения в условиях стохастической неопределенности можно описать с помощью матрицы «выигрышей» (или «потерь») c m возможными действиями (стратегиями) 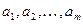 и n возможными случайными состояниями природы
и n возможными случайными состояниями природы 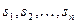 , которая имеет вид:
, которая имеет вид:
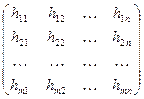 ,
,
где 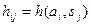 представляется как выигрыш (потеря), связанный с
представляется как выигрыш (потеря), связанный с 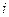 -ой стратегией ЛПР (игрока) и
-ой стратегией ЛПР (игрока) и 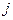 -м состоянием природы.
-м состоянием природы.
При решении задач наряду матрицами рассматривают соответствующие таблицы:
| Таблица 5.1. Исходная матрица в условиях неопределенности | ||||
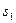 | 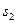 | … | 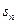 | |
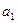 | 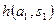 | 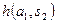 | … | 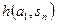 |
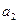 | 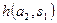 | 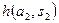 | … | 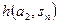 |
| … | … | … | … | … |
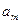 | 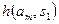 | 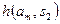 | … | 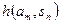 |
Для 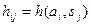 используют также термин: «полезность» принятого решения.
используют также термин: «полезность» принятого решения.
Таким образом, требуется найти вектор 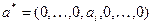 , который обеспечивает оптимум заданной функции полезности
, который обеспечивает оптимум заданной функции полезности 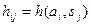 по некоторому критерию.
по некоторому критерию.
В условиях неопределенности вероятностное распределение, соответствующее состояниям природы, не известно. Поэтому выбор стратегии игроком принимается на основе ряда критериев:
1. Критерий Лапласа.
2. Максиминный (минимаксный) критерий.
3. Максимаксный критерий.
4. Критерий Гурвица.
5. Критерий Сэвиджа.
Критерий Лапласа опирается на следующее соображение: так как распределение вероятностей состояний среды неизвестно, можно считать их равными, то есть 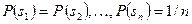 .
.
Выбор наилучшей стратегии выбирается на основе критерия максимизации выигрыша, если 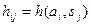 задает выигрыш:
задает выигрыш:
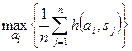 , (5.1)
, (5.1)
или минимизации потерь, если 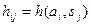 задает потерю:
задает потерю:
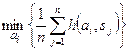 , (5.2)
, (5.2)
Пример T578. Хенк — прилежный студент, который обычно получает хорошие отметки благодаря, в частности, тому, что имеет возможность повторить материал в ночь перед экзаменом. Перед завтрашним экзаменом Хенк столкнулся с небольшой проблемой. Его сокурсники организовали на всю ночь вечеринку, в которой он хочет участвовать. Хенк имеет три альтернативы: 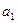 — участвовать в вечеринке всю ночь;
— участвовать в вечеринке всю ночь; 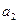 — половину ночи участвовать в вечеринке, а половину — учиться;
— половину ночи участвовать в вечеринке, а половину — учиться; 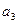 — учиться всю ночь.
— учиться всю ночь.
Профессор, принимающий завтрашний экзамен, непредсказуем, и экзамен может быть легким ( 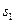 ), средним (
), средним ( 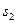 ) или трудным (
) или трудным ( 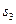 ). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно ожидать следующие баллы.
). В зависимости от сложности экзамена и времени, затраченного Хенком на повторение, можно ожидать следующие баллы.
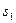 | 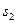 | 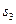 | |
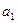 | |||
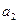 | |||
 |
Порекомендуйте Хенку, какой выбор он должен сделать.
Решение. Очевидно, что в данном случае необходимо воспользоваться формулой (5.1), чтобы максимизировать полученный балл. Рассчитаем ожидаемые значения баллов для каждого решения (стратегии):
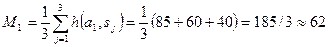 балла,
балла,
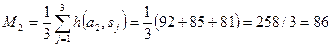 баллов,
баллов,
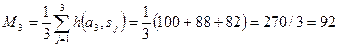 балла.
балла.
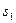 | 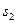 | 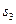 | М | |
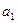 | ||||
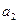 | ||||
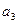 |
Лаплас рекомендует учиться всю ночь.
Максиминный (минимаксный) критерийназывают еще критерием Вальда, или критерием «осторожного наблюдателя», так как предполагается, что внешняя среда находится в самом невыгодном положении. Поэтому критерий сводится к выбору наилучшей альтернативы из наихудших, если 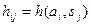 задает прибыль (максиминный критерий):
задает прибыль (максиминный критерий):
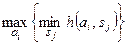 , (5.3)
, (5.3)
или к выбору наихудшей альтернативы из наилучших, если 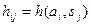 задает потери (минимаксный критерий):
задает потери (минимаксный критерий):
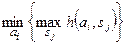 , (5.4)
, (5.4)
Применим критерии к предыдущей задаче.
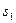 | 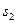 | 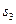 | 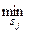 | |
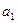 | ||||
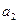 | ||||
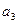 |
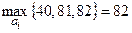 , критерий предлагает стратегию
, критерий предлагает стратегию 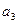 , оценивая при этом шансы Хенка, как получение 82 баллов, при условии, что он будет учиться всю ночь.
, оценивая при этом шансы Хенка, как получение 82 баллов, при условии, что он будет учиться всю ночь.
Максимаксный критерийназывают также критерием «здорового оптимиста», так как предполагается, что внешняя среда находится в самом выгодном положении. Поэтому критерий сводится к выбору наилучшей альтернативы из наилучших, если 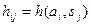 задает выигрыш:
задает выигрыш:
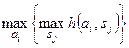 , (5.5)
, (5.5)
Применим критерий к предыдущей задаче.
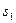 | 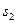 | 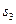 | 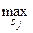 | |
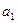 | ||||
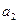 | ||||
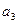 |
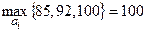 , критерий предлагает стратегию
, критерий предлагает стратегию 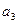 , оценивая при этом шансы Хенка, как получение 100 баллов, при условии, что он будет учиться всю ночь.
, оценивая при этом шансы Хенка, как получение 100 баллов, при условии, что он будет учиться всю ночь.
Критерий Гурвица предполагает, что внешняя среда может находиться в наилучшем состоянии с вероятностью 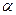 , а в наихудшем состоянии с вероятностью
, а в наихудшем состоянии с вероятностью 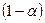 , где
, где 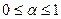 .
.
Если 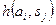 задает выигрыш, тогда решение по критерию Гурвица производится по условию:
задает выигрыш, тогда решение по критерию Гурвица производится по условию:
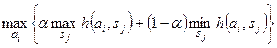 , (5.6)
, (5.6)
Если 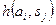 задает потери, тогда решение по критерию Гурвица производится по условию:
задает потери, тогда решение по критерию Гурвица производится по условию:
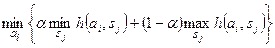 , (5.7)
, (5.7)
Параметр 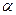 называют показателем оптимизма, так как выбором параметра можно задавать степень оптимизма. При
называют показателем оптимизма, так как выбором параметра можно задавать степень оптимизма. При 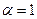 критерий Гурвица переходит в критерий оптимиста, а при
критерий Гурвица переходит в критерий оптимиста, а при 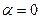 — в критерий пессимиста.
— в критерий пессимиста.
Рассмотрим решение предыдущей задачи с уровнем оптимизма 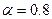 . Ожидаемое значения баллов для стратегии
. Ожидаемое значения баллов для стратегии 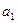 :
:
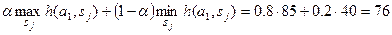 .
.
Аналогично рассчитаем значения для остальных стратегий. Для сравнения приведем результаты расчетов при различных 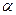 :
:
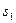 | 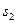 | 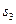 | 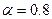 | 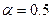 | 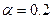 | |
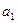 | 62,5 | |||||
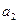 | 89,8 | 86,5 | 83,2 | |||
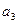 | 96,4 | 85,6 | ||||
| max: | 96,4 | 85,6 |
Наилучшим решением и для данного критерия является 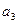 .
.
Критерий Сэвиджа строится на основе матрицы «потерь» 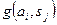 , которая получается из матрицы платежей (выигрышей или проигрышей) следующим образом:
, которая получается из матрицы платежей (выигрышей или проигрышей) следующим образом:
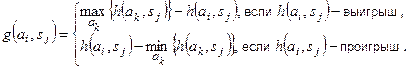
Построим матрицу потерь для рассматриваемого выше примера. В данном случае 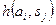 задает выигрыш. Поэтому найдем максимальные значения по столбцам:
задает выигрыш. Поэтому найдем максимальные значения по столбцам:
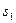 | 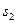 | 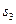 | |
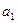 | |||
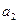 | |||
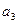 | |||
| max |
Вычтем полученные числа 100, 88, 82 из элементов соответствующих столбцов, получим матрицу потерь:
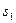 | 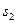 | 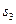 | |
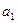 | |||
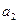 | |||
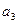 | |||
| max |
К полученной матрице применяется минимаксный критерий:
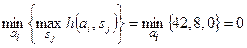 ,
,
что соответствует решению 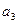 .
.
