Анализ модели. Составление пары симметричных двойственных задач
В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи)
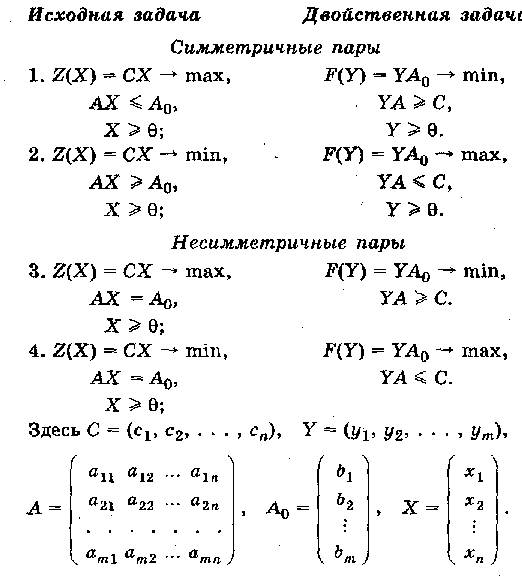
Правила составления двойственных задач:
1.Во всех ограничениях исходной задачи свободные члены должны находиться в правой части, а члены с неизвестными — в левой.
2. Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.
3. Если знаки неравенств в ограничениях исходной задачи «≤», то целевая функция Z(X) = с0 + с1 · x1 + с2 · x2 + … + сn · xn должна максимизироваться, а если «≥», то минимизироваться.
4. Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.
5. Целевая функция двойственной задачи имеет вид
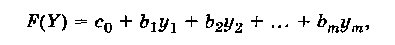
где с0 — свободный член целевой функции Z(X) исходной задачи, b1, b2, …, bm,— свободные члены в ограничениях исходной задачи, при этом bi— свободный член именно того ограничения исходной задачи, которому соответствует неизвестная yi, a y1, y2, …, ym— неизвестные в двойственной задаче.
6. Целевая функция F(Y) двойственной задачи должна оптимизироваться противоположным по сравнению с Z(X) образом, т.е. если Z(X) → max, то
F(Y)→ min, и если Z(X) → min, то F(Y) → max.
7. Каждому неизвестному хj, j = 1, 2, ..., п исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих п ограничений (вместе с условиями неотрицательности неизвестных yi, соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными yi у2, ..., ут — в левых. Все знаки неравенств имеют вид «≥», если F(Y) → min, и «≤», если
F(Y) → max.
Коэффициенты, с которыми неизвестные yl у2, …, ут входят в ограничение, соответствующее неизвестному xj, совпадают с коэффициентами при этом неизвестном х. в ограничениях исходной задачи, а именно: коэффициент при yiсовпадает с тем коэффициентом при хj с которым хj входит в ограничение исходной задачи, соответствующее неизвестному yi.
Двойственность
1) Составляем матрицу из полученной математической модели
7 6 2 1
А = 1 3 6 1
0 2 5 1
1 1 1 F
2) Транспонируем матрицу A
7 1 0 1
А-1 = 6 3 2 1
2 6 5 1
1 1 1 Z
3) Составляем двойственную задачу
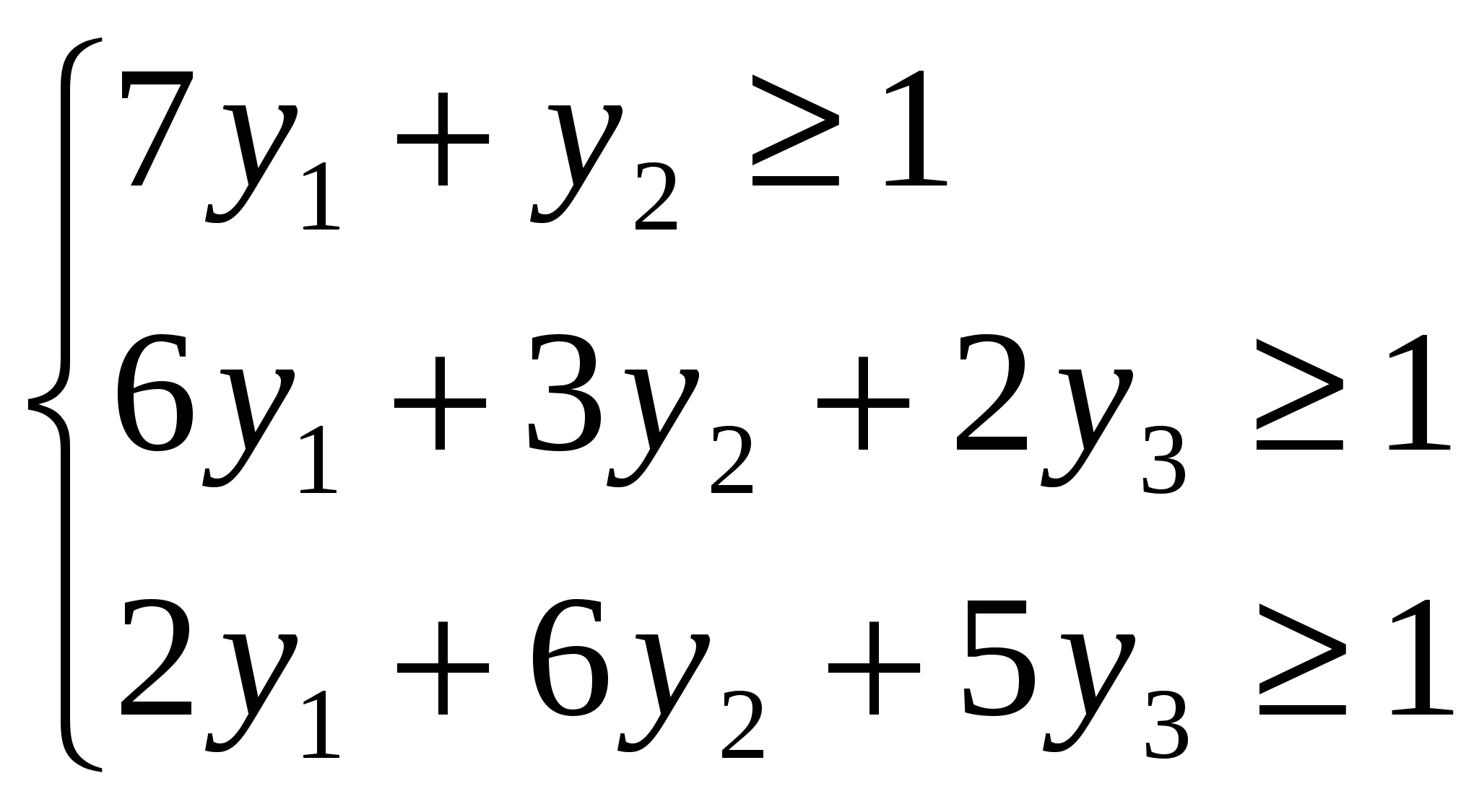
Z = y1 + y2 +y3 → Min
Вот и получили пару симметричных двойственных задач. Задача на максимум и на минимум
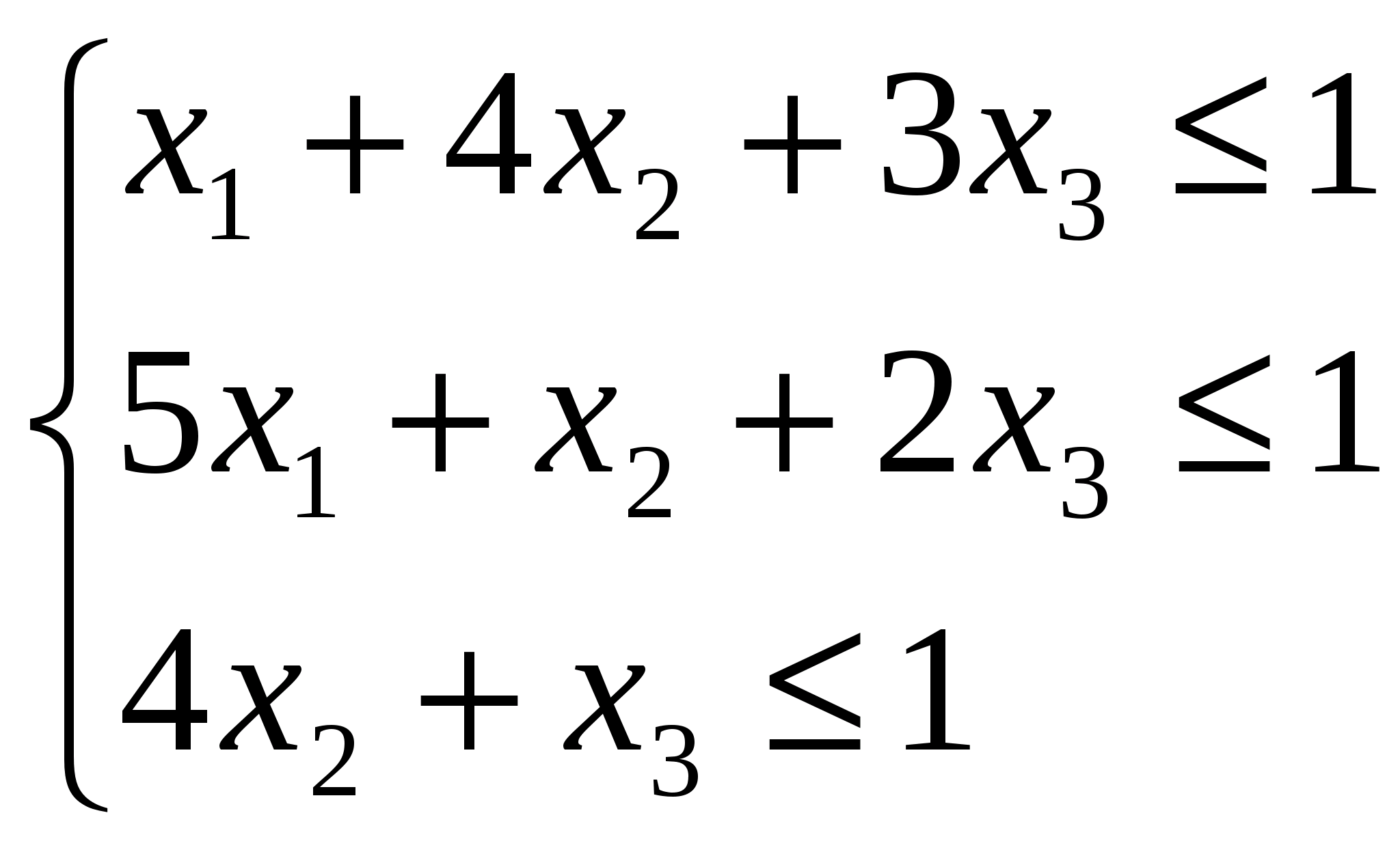
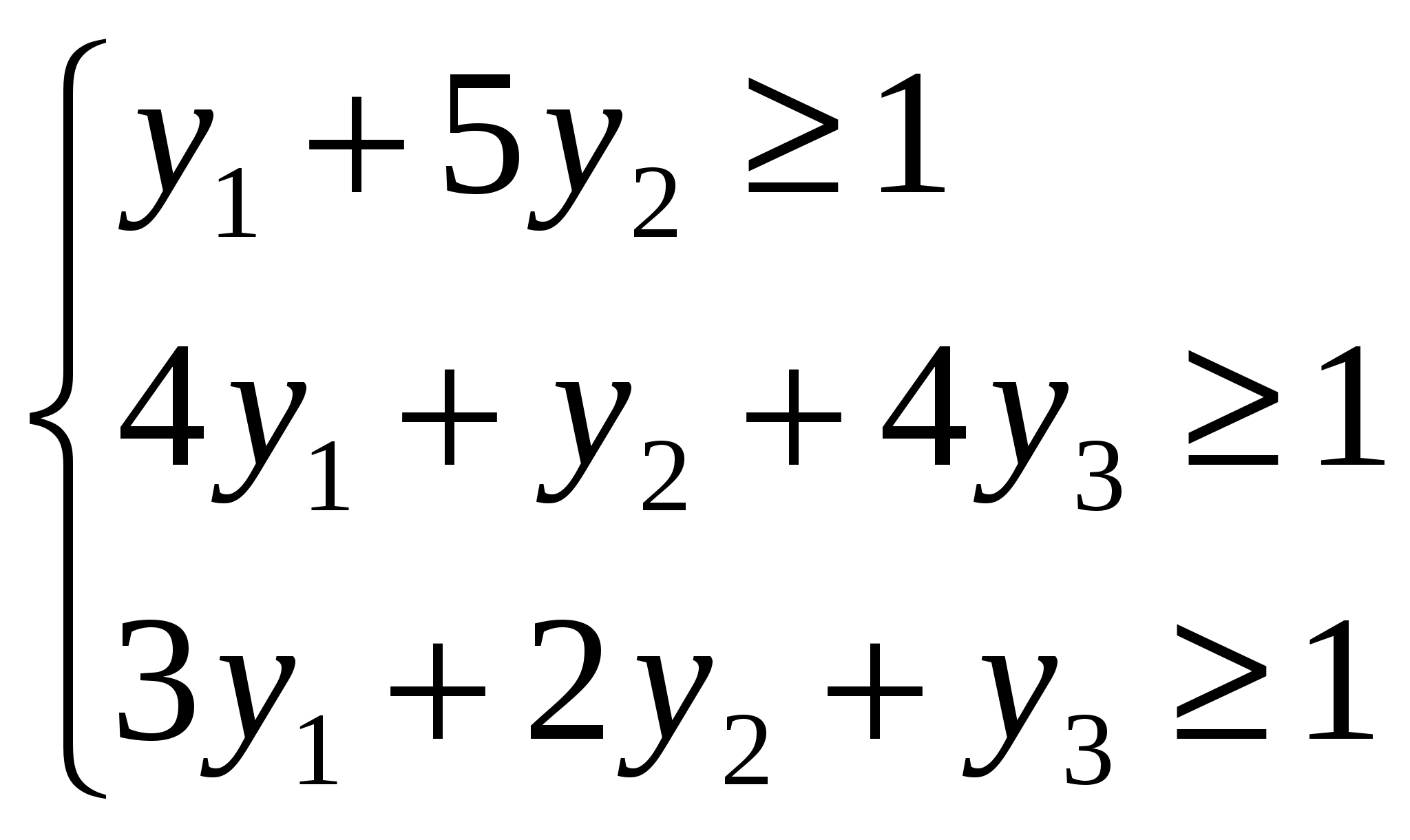
F(x) = x1 + x2 + x3 → max Z(x) = y1 + y2 +y3 → min
