Вычисление определенных интегралов по формуле трапеций и формуле Симпсона.
1. Вычислить интеграл по формуле трапеций с тремя десятичными знаками. 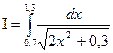
Решение: Для достижения заданной степени точности необходимо определить значение n max,
чтобы: 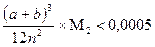 (*) Здесь a=0.7; b=1,3;
(*) Здесь a=0.7; b=1,3; 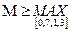 / f ”(x)/,
/ f ”(x)/,
где f (x)=1/ 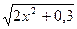

Находим: f ’(x)= 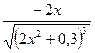 , f ”(x)=
, f ”(x)= 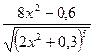 ;
;
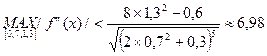
Положим M2=7, тогда неравенство (*) примет вид 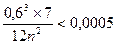
Откуда n2>252, т.е. n>16; возьмем n=20, Вычисление интеграла производим по формуле: 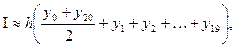 где: h=(b-a)/n=0,6/20=0,03, yi=y(xi)=1/
где: h=(b-a)/n=0,6/20=0,03, yi=y(xi)=1/ 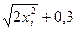 ; xi=0,7+ih (i=0,1,2,…,20) Все расчеты произведены в таблице:
; xi=0,7+ih (i=0,1,2,…,20) Все расчеты произведены в таблице:
Таблица 1.
| i | xi | xi2 | 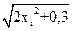 2xi2+0,3 2xi2+0,3 | 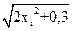 | y0,y20 | y1,…,y19 |
| 0,7 | 0,49 | 1,28 | 1,131371 | 0,883883 | ||
| 0,73 | 0,5329 | 1,3658 | 1,168674 | 0,85567 | ||
| 0,76 | 0,5776 | 1,4552 | 1,206317 | 0,82897 | ||
| 0,79 | 0,6241 | 1,5482 | 1,244267 | 0,803686 | ||
| 0,82 | 0,6724 | 1,6448 | 1,282498 | 0,779729 | ||
| 0,85 | 0,7225 | 1,745 | 1,320984 | 0,757011 | ||
| 0,88 | 0,7744 | 1,8488 | 1,359706 | 0,735453 | ||
| 0,91 | 0,8281 | 1,9562 | 1,398642 | 0,714979 | ||
| 0,94 | 0,8836 | 2,0672 | 1,437776 | 0,695519 | ||
| 0,97 | 0,9409 | 2,1818 | 1,477092 | 0,677006 | ||
| 2,3 | 1,516575 | 0,65938 | ||||
| 1,03 | 1,0609 | 2,4218 | 1,556213 | 0,642585 | ||
| 1,06 | 1,1236 | 2,5472 | 1,595995 | 0,626568 | ||
| 1,09 | 1,1881 | 2,6762 | 1,63591 | 0,611281 | ||
| 1,12 | 1,2544 | 2,8088 | 1,675947 | 0,596677 | ||
| 1,15 | 1,3225 | 2,945 | 1,7161 | 0,582717 | ||
| 1,18 | 1,3924 | 3,0848 | 1,75636 | 0,569359 | ||
| 1,21 | 1,4641 | 3,2282 | 1,796719 | 0,55657 | ||
| 1,24 | 1,5376 | 3,3752 | 1,837172 | 0,544315 | ||
| 1,27 | 1,6129 | 3,5258 | 1,877711 | 0,532563 | ||
| 1,3 | 1,69 | 3,68 | 1,918333 | 0,521286 | ||
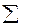 | 1,40517 | 12,77004 |
Таким образом,
I=0,03 ( 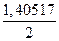 +12,77004)=0,40418»0,404
+12,77004)=0,40418»0,404
2) Пусть n=8, поэтому h=(b-a)/n=(1,6-1,2)/8=0,05.
Вычислительная формула:
I= 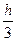 (y0+4y1+2y2+4y3+2y4+4y5+2y6+4y7+y8), где yi=y(xi)=
(y0+4y1+2y2+4y3+2y4+4y5+2y6+4y7+y8), где yi=y(xi)= 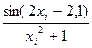 , xi=1,2+ih
, xi=1,2+ih
Вычисление значений функции, а также сложение значений функции, имеющих одинаковые коэффициенты в формуле, производим в таблице 2.
Таблица 2.
| / | xi | 2xi-2,l | sin (2xi-2,1) | xi2+1 | y0,y8 | y1, y3, y5, y7 | y2, y4, y6 |
| 0 | 1,20 | 0,30 | 0,29552 | 2,44 | 0,1211 | ||
| 1 | 1,25 | 0,40 | 0,38942 | 2,5625 | 0,1520 | ||
| 2 | 1,30 | 0,50 | 0,4794 | 2,69 | 0,1782 | ||
| 3 | 1,35 | 0,60 | 0,5646 | 2,8225 | 0,2000 | ||
| 4 | 1,40 | 0,70 | 0,6442 | 2,96 | 0,2176 | ||
| 5 | 1,45 | 0,80 | 0,7174 | 3,1024 | 0,2312 | ||
| 6 | 1,50 | 0,90 | 0,7833 | 3,25 | 0,2410 | ||
| 7 | 1,55 | 1,00 | 0,8415 | 3,4025 | 0,2473 | ||
| 8 | 1,60 | 1,10 | 0.8912 | 3,56 | 0,2503 | ||
| S | 0,3713 | 0,8305 | 0,6368 |
Следовательно, I» 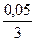 (0,3714+4 •0,8305+2 • 0,6368) »0,88278.Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. 3).
(0,3714+4 •0,8305+2 • 0,6368) »0,88278.Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. 3).
Так как max |D4yi|=0,0001, то остаточный член формулы
Rост< 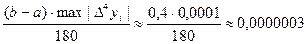
Вычисления производились с четырьмя значащими цифрами, а потому величина остаточного члена на погрешность не влияет.
Погрешность вычислений можно оценить из соотношения
DI = (b -a) •Dу < 0,4 • 0,0001 < 0,00005. Значит, полученные четыре десятичных знака верны.
Таблица 3.
| I | уi | Dyi | D2yi | D3yi | D4yi |
| 0 | 0,1211 | 0,0309 | -0,0047 | 0,0003 | -0,0001 |
| 1 | 0,1520 | 0,0262 | -0,0044 | 0,0002 | 0.0000 |
| 2 | 0,1782 | 0,0218 | -0,0042 | 0,0002 | 0.0000 |
| 3 | 0,2000 | 0,0176 | -0,0040 | 0,0002 | 0,0001 |
| 4 | 0,2176 | 0,0136 | -0,0038 | 0,0003 | -0,0001 |
| 5 | 0,2312 | 0.0098 | -0,0035 | 0,0002 | |
| 6 | 0,2410 | 0,0063 | -0,0033 | ||
| 7 | 0,2473 | 0,0030 | |||
| 8 | 0,2503 |
Самостоятельно:
1) 
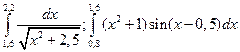
2) 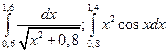
3) 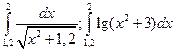
4) 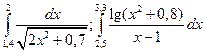
5) 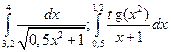
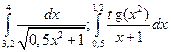
Лабораторная работа.
Вычисление определенных интегралов по формуле левых, правых и средних прямоугольников.
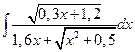 -?
-?
Для вычисления по формулам левых, правых и средних прямоугольников при n=10 разобьём отрезок интегрирования [1,5;2,3] на 10 частей с шагом 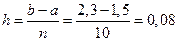 . Составим таблицу значений подинтегральной функции в точках деления отрезка:
. Составим таблицу значений подинтегральной функции в точках деления отрезка:
| i | xi |  0,3xi+1,2 0,3xi+1,2 |  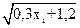 |  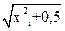 |  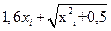 | yi |
| 1,5 | 1,65 | 1,284523 | 1,658312 | 4,058312 | 0,316517 | |
| 1,58 | 1,674 | 1,293832 | 1,731011 | 4,259011 | 0,303787 | |
| 1,66 | 1,698 | 1,303073 | 1,804328 | 4,460328 | 0,292147 | |
| 1,74 | 1,722 | 1,31225 | 1,878191 | 4,662191 | 0,281466 | |
| 1,82 | 1,746 | 1,321363 | 1,952537 | 4,864537 | 0,271632 | |
| 1,9 | 1,77 | 1,330413 | 2,027313 | 5,067313 | 0,262548 | |
| 1,98 | 1,794 | 1,339403 | 2,102475 | 5,270475 | 0,254133 | |
| 2,06 | 1,818 | 1,348332 | 2,177981 | 5,473981 | 0,246317 | |
| 2,14 | 1,842 | 1,357203 | 2,253797 | 5,677797 | 0,239037 | |
| 2,22 | 1,866 | 1,366016 | 2,329893 | 5,881893 | 0,232241 | |
| 2,3 | 1,89 | 1,374773 | 2,406242 | 6,086242 | 0,225882 | |
 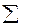 | 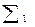 | 2,699825 | ||||
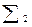 | 2,60919 |
В таблице найдены суммы: 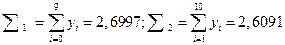
По формуле левых прямоугольников 
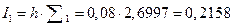
По формуле правых прямоугольников 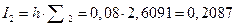
Эти значения отличаются уже в сотых долях. За окончательное значение примем полусумму найденных значений, округлив результат до тысячных: 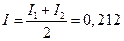

2) 
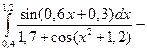 ?
?
Для решения воспользуемся формулой средних прямоугольников: 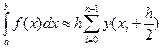
Вычисления производим с шагом h=(b-a)/10=(1,2-0,4)/10=0,08.
| i | xi | Xi+h/2 | Sin(0,6x+0,3) | 1,7+cos(x2+1,2) | Y(xi+h/2) |
| 0,4 | 0,44 | 0,534571 | 1,909239 | 0,279992 | |
| 0,48 | 0,52 | 0,574506 | 1,839936 | 0,312242 | |
| 0,56 | 0,6 | 0,613117 | 1,757165 | 0,348924 | |
| 0,64 | 0,68 | 0,650316 | 1,661206 | 0,391472 | |
| 0,72 | 0,76 | 0,686017 | 1,552932 | 0,441756 | |
| 0,8 | 0,84 | 0,720137 | 1,434036 | 0,502175 | |
| 0,88 | 0,92 | 0,752599 | 1,307265 | 0,575705 | |
| 0,96 | 0,783327 | 1,176628 | 0,665739 | ||
| 1,04 | 1,08 | 0,812251 | 1,047557 | 0,775376 | |
| 1,12 | 1,16 | 0,839303 | 0,92697 | 0,905426 | |
| 1,2 | 5,198807 |
Приближённое значение интеграла:
I=h 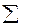 =0,1×5,198807=0,43580
=0,1×5,198807=0,43580
Самостоятельно:
1) 
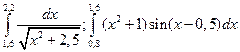
2) 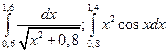
3) 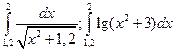
4) 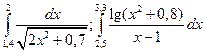
5) 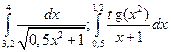
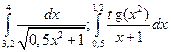
Лабораторная работа.
Задание: Используя метод Эйлера с уточнением, составить таблицу приближенных значений интеграла дифференциального уравнения y=f(x,y), удовлетворяющего начальным условиям y (x0)=y0 на отрезке [a,b]; шаг h=0,1. Все вычисления вести с четырьмя десятичными знаками.
Образец выполнения:
y¢=x+sin(y/2,25); y0(1,4)=2,2, xÎ[1,4;2,4]
Метод Эйлера с уточнением заключается в том, что каждое значение yk+1=y(xk+1), где y(x) — искомая функция, а xk+1=x0+h(k+1), k=0, 1, 2 …, определяется следующим образом:
За начальное приближение берется
y(0)k+1=yk+hf(xk, yk), где f(x, y)=y¢(x, y)
найденное значение y(0)k+1 уточняется по формуле
y(i)k+1=yk+h/2[f(xk, yk)+ f(xk+1, yk+1)] (i=1, 2…)
Уточнение продолжают до тех пор, пока в пределах требуемой точности два последовательных приближения не совпадут.
Все описанные вычисления удобно производить, составив следующие таблицы:
q Основную таблицу, в которой записывается ответ примера (таблица I);
q Таблицу, в которой выполняется процесс последовательных приближений (таблица II);
q Вспомогательную таблицу, в которой вычисляются значения функции f(xk, yk) (таблица III).
| Таблица I | ||||
| k | xk | yk | fk=f(xk, yk) | hfk |
| 0 | 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 | 2,2 2,4306 2,6761 2,9357 3,2084 3,4929 3,7876 4,0908 4,4006 4,7152 5,0328 | 2,2292 2,3821 2,5281 2,6648 2,7895 2,8998 2,9936 3,0696 3,1268 3,1654 | 0,2229 0,2382 0,2528 0,2665 0,2790 0,2900 0,2994 0,3070 0.3127 0.3165 |
Таблица II
| k+1 | xk+1 | yk | i | y k+1 | fk | f k+1 | fk+f k+1 | h/2(fk+f k+1) |
| 1,5 | 2,2 | 2,4229 | 2,2292 | 2,3805 | 4,6097 | 0,2305 | ||
| 2,4305 | 2,3820 | 4,6112 | 0,2306 | |||||
| 2,4306 | 2,3821 | 4,6113 | 0,2306 | |||||
| 1,6 | 2,4306 | 2,6688 2,6760 2,6761 | 2,3821 | 2,5268 2,5280 2,5281 | 4,9089 4,9101 4,9102 | 0,2454 0,2455 0,2455 | ||
| 1,7 | 2,6761 | 2,9289 2,9357 | 2,5281 | 2,6641 2,6648 | 5,1922 5,1929 | 0.2596 0,2596 | ||
| 1,8 | 2,9357 | 3,2022 3,2084 | 2,6648 | 2,7892 2,7895 | 5,4540 5,4543 | 0,2727 0,2727 | ||
| 1,9 | 3,2084 | 3,4874 3,4929 | 2,7895 | 2,8998 2,8998 | 5,6893 5,6893 | 0,2845 0,2845 | ||
| 2,0 | 3,4929 | 3,7829 3,7876 | 2,8998 | 2,9939 2,9936 | 5,8937 5,8934 | 0,2947 0,2947 | ||
| 2,1 | 3,7876 | 4,0870 4,0908 | 2,9936 | 3,0700 3,0696 | 6,0636 6,0632 | 0,3032 0,3032 | ||
| 2,2 | 4,0908 | 4,3978 4,4006 | 3,0696 | 3,1273 3,1268 | 6,1969 6,1964 | 0.3098 0.3098 | ||
| 2,3 | 4,4006 | 4,7133 4,7152 | 3,1268 | 3,1658 3,1654 | 6,2926 6,2922 | 0.3146 0.3146 | ||
| 2,4 | 4,7152 0 | 5,0517 5,0328 | 3,1654 | 3,1866 3,1863 | 6,3520 6,3517 | 0,3176 0,3176 |
Ответом являются значения yk(x), полученные в табл. I.
Варианты заданий:
1. y¢=x+cos 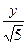 , y0(1,8)=2,6, xÎ[1,8;2,8]
, y0(1,8)=2,6, xÎ[1,8;2,8]
2. y¢=x+cos 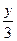 , y0(1,6)=4,6, xÎ[1,6;2,6]
, y0(1,6)=4,6, xÎ[1,6;2,6]
3. y¢=x+cos 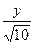 , y0(0,6)=0,8, xÎ[0,6;1,6]
, y0(0,6)=0,8, xÎ[0,6;1,6]
4. y¢=x+cos 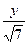 , y0(0,5)=0,6, xÎ[0,5;1,5]
, y0(0,5)=0,6, xÎ[0,5;1,5]
