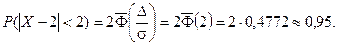Плотность распределения

Пример. Случайная величина подчинена закону распределения с плотностью:

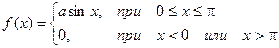
Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до .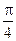

Построим график плотности распределения:

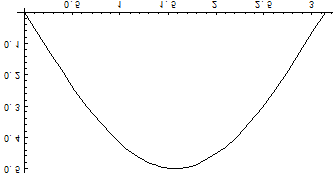
Для нахождения коэффициента а воспользуемся свойством .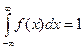

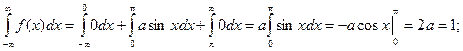
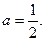
Находим вероятность попадания случайной величины в заданный интервал.

Пример. Задана непрерывная случайная величина х своей функцией распределения f(x).

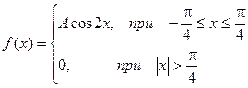
Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал .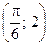

Найдем коэффициент А.

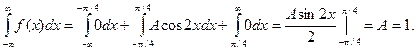
Найдем функцию распределения:

1) На участке :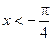

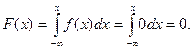
2) На участке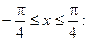

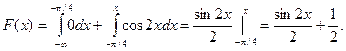
3) На участке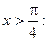

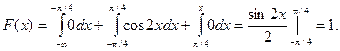
Итого: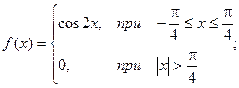

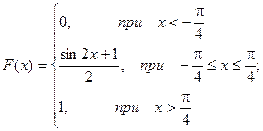
Построим график плотности распределения:

f(x)

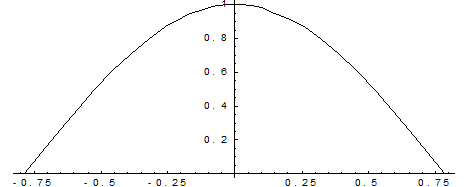
Построим график функции распределения:

F(x)

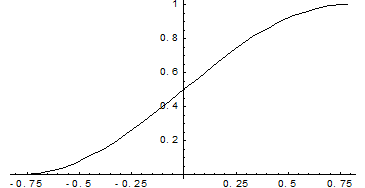
Найдем вероятность попадания случайной величины в интервал .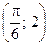

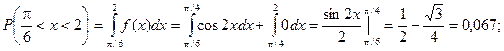
Ту же самую вероятность можно искать и другим способом:

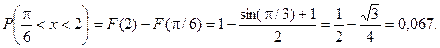
Числовые характеристики непрерывных случайных величин.

Пример. Для рассмотренного выше примера определить математическое ожидание и дисперсию случайной величины Х.

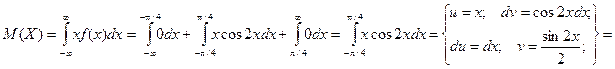
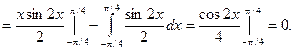
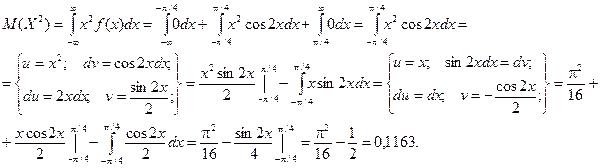
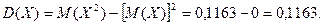
Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.

Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).

Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна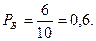

Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз.

Для составления закона распределения надо найти вероятности каждого из этих событий.

1) Белый шар не появился вовсе: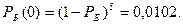

2) Белый шар появился один раз: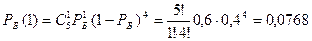

3) Белый шар появиться два раза: .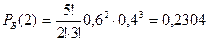

4) Белый шар появиться три раза: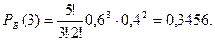

5) Белый шар появиться четыре раза: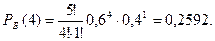

6) Белый шар появился пять раз: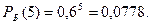

Получаем следующий закон распределения случайной величины Х.

х
х2
р(х)	0,0102	0,0768	0,2304	0,3456	0,2592	0,0778

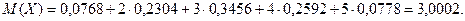
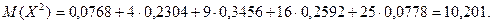
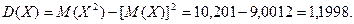
Функция Лапласа.

Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.

Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т.

Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально.

Получаем:

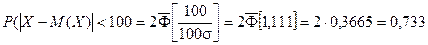
Пример. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и s = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность распределения имеет вид:

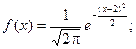
Построим график:

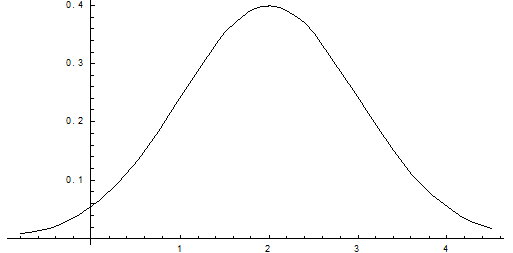
Найдем вероятность попадания случайной величины в интервал (1; 3).

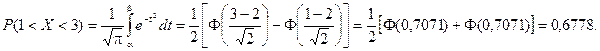
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2.

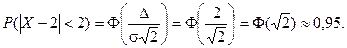
Тот же результат может быть получен с использованием нормированной функции Лапласа.