Графический анализ на чувствительность

После того как оптимальное решение ЗЛП найдено можно поставить дополнительные вопросы [Таха 1]:

- насколько можно сократить или увеличить запасы ресурсов и как это отразится на значении целевой функции;

- изменение какого из ресурсов наиболее выгодно;

- в каких пределах допустимо изменение коэффициентов целевой функции, при которых оптимальное значение целевой функции не изменяется.

Исследование влияния изменения параметров исходной ЗЛП на полученное оптимальное решение называется анализом на чувствительность.

Если количество переменных ЗЛП равно двум, исследование на чувствительность можно провести графическим методом.

Рассмотрим задачу, решенную в п. 1.2. Напомним условие: при производстве двух товаров А и В используется три вида ресурсов: R1, R2, R3, требуется максимизировать прибыль. Таким образом, имеются три ограничения на ресурсы.

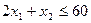, (ресурс R₁) (1)

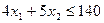, (ресурс R₂) (2)

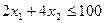, (ресурс R₃) (3)

Ограничения на ресурсы делят на две группы — активные (связывающие) и неактивные (несвязывающие), а соответствующие им ресурсы называют дефицитными и недефицитными. Активным ограничениям соответствуют прямые, ограничивающие область допустимых планов 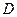и проходящие через оптимальную точку.

Дефицитные ресурсы в оптимальной точке используются полностью, а недефицитные имеются в некотором избытке.

1. Интервалы устойчивости оптимального плана по отношению к изменению неактивных ограничений. Так как недефицитный ресурс имеется в некотором избытке, представляет интерес найти предельно допустимое уменьшение объемов этого ресурсов, которое не меняет найденное оптимальное значение целевой функции.

В нашем случае ресурсы R2 и R3 являются активными, а ресурс R1 — неактивным. На рис. 1.5. в круглых скобках указан номер соответствующего ресурса.

Продолжим прямую АС, соответствующую неактивному ограничению 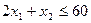(1), и перенесем ее параллельно самой себе до пересечения с точкой D. Значение ресурса R1 в точке D равно 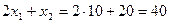, максимальное уменьшение ресурса 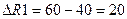. Таким образом, запасы ресурса R1 можно уменьшить на 20 единиц, значение целевой функции при этом не изменится.

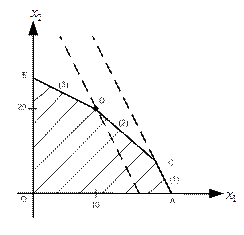
Рис. 1.5. Уменьшение объема недефицитного ресурса R1

2. Оценки ограничений на дефицитные ресурсы.Дефицитные ресурсы в оптимальной точке используются полностью. Так как сокращение объема дефицитного ресурса не улучшает оптимальное значение целевой функции, представляет интерес выяснить, на сколько можно увеличить запас дефицитного ресурса для улучшения оптимального плана. Напомним, что найденное оптимальное значение целевой функции 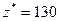у.е.

Рассмотрим дефицитный ресурс R2 и соответствующее ему активное ограничение 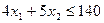(2). На рис. 1.6. этому ограничению соответствует прямая DC. Продолжим пунктирными линиями прямые ЕС и АС, соответствующие ограничениям (1) и (3). Они пересекутся в точке F. Прямую DC можно параллельным перемещением переместить так, чтобы она проходила через точку F. Таким образом, в этой точке все три ограничения становятся активными и оптимальная точка перемещается в точку F.

Найдем координаты точки F, решив систему:

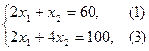(1.15)

Результат решения системы , .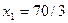

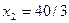Новый уровень запаса ресурса R2 при этом составит 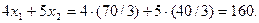Максимальное увеличение ресурса составит 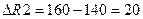единиц.

Как видно из рисунка 1.6, значение целевой функции при этом увеличится, так линия уровня целевой функции сместится в направлении градиента. Таким образом, запасы ресурса R2 можно увеличить на 20 единиц, оптимальное значение целевой функции при этом улучшится.

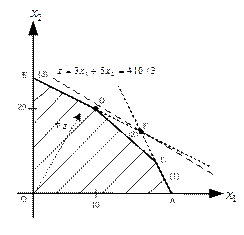
Рис. 1.6. Увеличение объема дефицитного ресурса R2

Доход составит 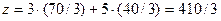у.е., прирост .

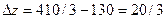Рассчитаем оценку ограничения на ресурс R2, характеризующую «вклад» дополнительной единицы ресурса в прирост максимального значения целевой функции.

Ценность дополнительной единицы ресурса равна отношению максимального приращения целевой функции к максимально допустимому приросту ресурса: .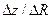

В нашем случае .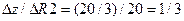

Рассмотрим дефицитный ресурс R3 и соответствующее ему активное ограничение 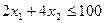(3). На рис. 1.7. этому ограничению соответствует прямая ED. Продолжим пунктирной линией прямую DС, соответствующую ограничению (2). Она пересечет ось в точке G c координатами .

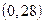Прямую ED тоже можно параллельным перемещением переместить так, чтобы она проходила через точку G. Таким образом, в этой точке все ограничения становятся активными и оптимальная точка перемещается в точку G.

Новый уровень запаса ресурса R3 составит 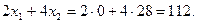Максимальное увеличение ресурса 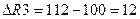единиц. Доход составит 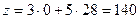у.е., прирост .

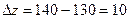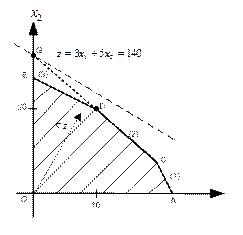
Рис. 1.7. Увеличение объема дефицитного ресурса R3

Оценка ограничения на ресурс R3 равна .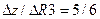

Для недефицитного ресурса R1 оценка равна нулю, так как .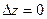

Подведем итоги оценки ресурсов:

Ресурс	Тип ресурса	Оценка
R1	Недефицитный
R2	Дефицитный	1/3
R3	Дефицитный	5/6

Ценность дополнительной единицы ресурса R2 = 1/3 у.е. на 1 единицу продукции. Ценность дополнительной единицы ресурса R3 = 5/6 у.е. на 1 единицу продукции. Следовательно, в первую очередь надо увеличивать ресурс R3.

3. Интервалы устойчивости для каждого коэффициента целевой функции. Рассмотрим, в каких пределах допустимо изменение коэффициентов целевой функции без изменения оптимального решения.

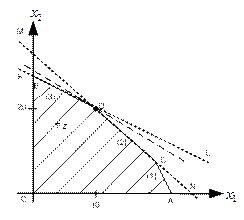
Рис. 1.8. Положение линия уровня, соответствующего оптимальному решению

На рис. 1.8. пунктиром изображена прямая, соответствующая линии уровня целевой функции, проходящей через оптимальную точку D. При изменении коэффициентов целевой функции, наклон прямой изменяется, оптимальное значение целевой функции при этом остается неизменным.

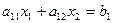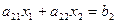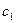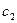Пусть активные ограничения (прямые линии) имеют вид и тогда интервалы изменения коэффициентов и целевой функции 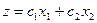, при которых точка D остается единственной оптимальной точкой, найдутся из условия:

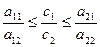или 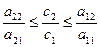. (1.16)

Линии MN 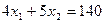и KL 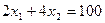на рис. 1.8. показывают возможные крайние положения линии целевой функции 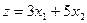, при которых точка D остается оптимальной.

В нашем случае 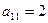, , 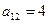, , 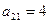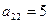выполнено 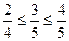. Следовательно, условия примут вид:

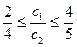или .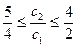

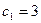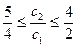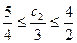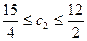Если один из коэффициентов, например, цена товара А , не изменяется, тогда интервал изменения второго коэффициента удобнее найти из условия , то есть Þ Þ .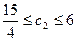

Значит, при сохранении цены на товар А, цену за единицу товара В можно увеличить до 6 у.е., то есть изменить ее на на 1 у.е., а можно сделать понизить цену до 15/4=3.75 у.е. Таким образом, можно определить интервал устойчивости коэффициента 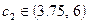, при котором оптимальное значение целевой функции и оптимальная точка D остаются неизменным. При 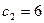оптимальными точками станут все точки отрезка DC.

Пусть теперь цена за единицу товара B остается постоянной, 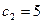, тогда интервал изменения первого коэффициента 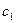удобнее искать из условия

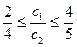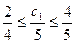Þ 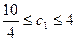Þ Þ .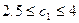

При сохранении цены на товар В цену за единицу товара А можно увеличить до 4 у.е., то есть изменить ее на на 1 у.е., или снизить цену до 2.5 у.е. Таким образом, можно определить интервал устойчивости коэффициента 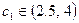, при котором оптимальное значение целевой функции остается неизменным. При 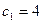оптимальными точками станут все точки отрезка ED.

Задача Т50.

Консервный завод Popeye перерабатывает за смену 60000 фунтов помидоров (7 пенсов центов за фунт) в томатный сок и пасту. Готовая продукция пакетируется в упаковки по 24 банки. Производство одной банки сока требует одного фунта спелых помидоров, а одной банки пасты — трети фунта. Заводской склад может принять за смену только 2000 упаковок сока и 6000 упаковок пасты. Оптовая цена одной упаковки томатного сока составляет 18 долл., одной упаковки томатной пасты — 9 долл.

Решите задачу графическим методом. Выпишите ответ оптимальный план и соответствующее значение целевой функции.

Обоснуйте, что найденный план — оптимальный.

Проведите исследование чувствительности найденного плана к изменению параметров задачи.

Укажите интервалы устойчивости для каждого коэффициента целевой функции.

Решение.Построим математическую модель задачи.

1). Искомые переменные задачи:

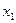— количество произведенных упаковок томатного сока;

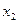— количество произведенных упаковок томатной пасты.

2). Ограничения задачи.

а) Ограничения на ресурсы. Расход используемых ресурсов не должен превышать их запас.

Первый ресурс задачи (R1) — объем помидоров, 60000 фунтов. Для производства одной упаковки томатного сока, которая вмещает 24 банки, требуется 24(банки) 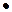1(фунт)=24 фунта спелых помидоров. Для производства одной упаковки пасты, которая вмещает тоже 24 банки, требуется 24(банки) 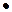1/3(фунт)=8 фунтов спелых помидоров. Следовательно, ограничение на первый ресурс имеет вид: .

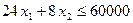Второй ресурс задачи (R2) — ресурс склада по приему упаковок сока, не более 2000 упаковок: .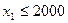

Третий ресурс задачи (R3) — ресурс склада по приему упаковок пасты, не более 6000 упаковок: .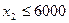

b) Ограничения на знак. Объемы производства не могут быть отрицательными.

, .

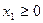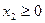3). Целевая функция 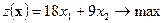максимизирует общую стоимость произведенной продукции.

Запишем математическую постановку задачи максимизации в стандартном виде:

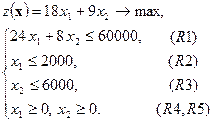
Или в виде:

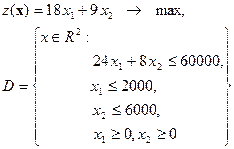
Графическое решение приведено на рис. 1.9.

Искомая область допустимого плана 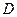ограничена многоугольником OACDE. Точка D является оптимальной точкой. Оптимальный план производства 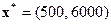, значение целевой функции 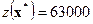долл.

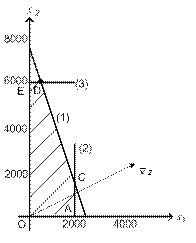
Рис. 1.9. Область допустимого плана

Покажем, что найденный план оптимален. Выпишем градиент целевой функции и внешние нормали прямых, ограничивающих допустимое множество.

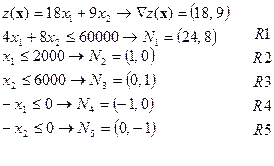
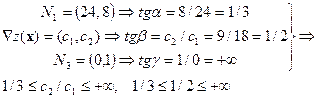
Оптимальная вершина D (точка пересечения ограничений R1 и R3) обладает тем свойством, что вектор-градиент целевой функции, вычисленный в этой точке, лежит внутри конуса (в двумерном случае — в пределах осевого сечения конуса), натянутого на вектора внешних нормалей к ограничивающим прямым, проходящим через точку D.

На рис. 1.10. показано, что вектор-градиент целевой функции 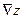лежит между векторами внешних нормалей к ограничивающим прямым ED и DC, проходящим через точку D. Следовательно, D — оптимальная вершина, найденный план оптимален.

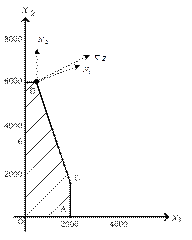
Рис. 1.10. Градиент целевой функции и внешние нормали прямых, ограничивающих область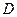

Проведем исследование чувствительности найденного плана к изменению параметров задачи.

Укажем сначала интервалы устойчивости для каждого коэффициента целевой функции.

Найденный при коэффициентах С=(18,9) оптимальный план 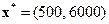остается оптимальным при выполнении условия: .

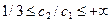Зафиксируем цену на томатный сок 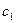=18, тогда 6≤ 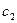≤ 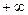. Допустимые изменения цены на пасту, при которых оптимальный план не улучшится D 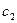= 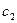- 9, D 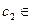[–3; ].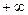

Если зафиксируем цену на пасту 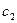=9, то 0≤ 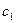≤27. Допустимые изменения цены на томатный сок D 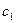= 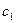–18, D 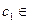[–18; 9].

Определим, какие ограничения задачи являются активными и неактивными. Так как оптимальная точка находится на пересечении прямых, соответствующих ограничениям R1 и R3, эти ограничения являются активными, здесь R1 — ограничение на ресурс сырья (помидоров), R3 — ограничение на ресурс склада по приему упаковок пасты.

Найдем интервалы устойчивостиоптимального плана по отношению к изменению неактивных ограничений.

Рассмотрим неактивное ограничение R2 на ресурс склада по приему упаковок сока.

При достаточно малом изменении правых частей неактивных ограничений найденный оптимальный план остается допустимым и оптимальным. Возникает вопрос:

На сколько единиц можно сократить правую часть неактивного ограничения, чтобы найденный оптимальный план мог быть реализован?

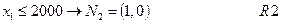
Из рис. 1.10 видно, что прямую АС можно перенести влево параллельно самой себе до пересечения с точкой D. Значение ресурса в точке А(2000,0) равно 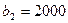, а в точке D(500,6000) равно .

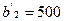Вычислим изменение ресурса D 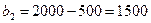. Объемы ресурса R1 можно уменьшить на 1500 единиц, при этом значение оптимального плана не изменится.

Заметим, что прямую АС можно перенести вправо параллельно самой себе на любой расстояние. При этом оптимальный план не изменится. Увеличение недефицитного ресурса не меняет значение оптимального плана.

Ограничение R2 может меняться от 500 до +¥, что не приводит к изменению оптимального плана. Результаты анализа правой части неактивного ограничения:

Ограничение	Интервал устойчивости оптимального плана	Изменение выручки	Оценка ресурса
R2=2000	Может меняться от 500 до +¥

Рассчитаем оценки ограничений на дефицитныересурсы, характеризующие «вклад» дополнительной единицы ресурса в прирост максимального значения целевой функции. R1 и R3 — активные ограничения на ресурсы.

Рассмотрим R1 – ограничение на ресурс сырья.

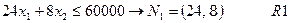
а). При увеличении объема ресурса R1.

Перенесем прямую (1), соответствующую ограничению R1, параллельно самой себе вправо (пунктирная линия). При этом все остальные ограничения остаются выполненными. Оптимальная точка D переместиться в точку F. Областью допустимых значений станет прямоугольник OAFE (рис. 1.11).

Рис. 1.11. Возможное изменение объема ресурса R1

Оптимальный план 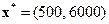также изменится, обозначим его .

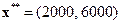Рассчитаем новый уровень запаса 24×2000+8×6000=96000, прирост запаса 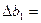96000-60000=36000. Значение целевой функции 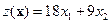=18×2000+9×6000=90000 и ее изменение 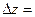90000-63000=27000.

Оценка ресурса равна 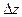/ 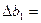27000/36000=0.75.

б). При уменьшении объема ресурса R1.

Перенесем прямую (1), параллельно самой себе влево (штрих-пунктирная линия) на рис. 1.11.

Оптимальная точка D переместиться в точку Е. Областью допустимых значений станет треугольник OAE.

Новый оптимальный план 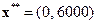, уровень запаса при этом составит 24×0+8×6000=48000, а прирост запаса — 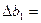48000-60000= -12000. Значение 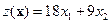=54000. Изменение значения целевой функции: 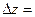54000-63000=-9000.

Оценка ресурса равна 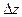/ 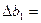-9000/(-12000)=0.75.

Рассмотрим R3 — ограничение на ресурс склада по количеству мест для хранения пасты:

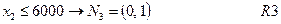
а). При увеличении объема ресурса R3.

Перенесем прямую (3), соответствующую ограничению R3, параллельно самой себе вверх (пунктирная линия). При этом все остальные ограничения остаются выполненными. Оптимальная точка D переместиться в точку F. Областью допустимых значений станет трапеция OAСF (рис. 1.12).

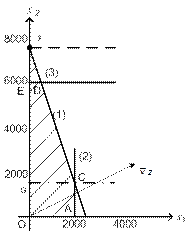
Рис. 1.12. Возможное изменение объема ресурса R3

Новый оптимальный план изменится: 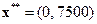. Уровень запаса при этом будет равен 7500, прирост запаса составит:

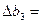7500-6000=1500.

Значение целевой функции 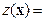18×0+9×7500=67500 и ее изменение составит 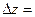67500-63000=4500. Оценка ресурса равна 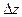/ 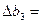4500/1500=3.

б). При уменьшении объема ресурса R3.

Перенесем прямую (3), соответствующую ограничению R3, параллельно самой себе вниз (штрих-пунктирная линия). При этом все остальные ограничения остаются выполненными. Оптимальная точка D переместиться в точку С. Областью допустимых значений станет прямоугольник OAСG (рис. 1.12).

Новый оптимальный план изменится: 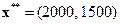. Новый уровень запаса равен 7500, прирост запаса — 1500, прирост запаса 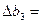1500-6000= -4500.

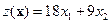=18×2000+9×1500=495000,

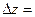49500-63000=-13500.

Оценка ресурса равна 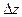/ 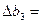-13500/(-4500)= 3.

Оценка ресурсов:

Ресурс	Тип ресурса	Оценка
R1	Дефицитный	0.75
R2	Недефицитный
R3	Дефицитный

Подведем итог. Ценность дополнительной единицы ресурса R1 = 0.75 долларов на 1 фунт спелых помидоров. То есть при увеличении запасов сырья (спелых помидоров) на 1 фунт прибыль увеличиться на 0.75 долларов.

Ценность дополнительной единицы ресурса R3 = 3 долларов на 1 дополнительное место для хранения упаковок пасты.

Следовательно, в первую очередь надо увеличивать ресурс R3 — количество мест на складе для хранения упаковок пасты.

Количество мест на складе для хранения упаковок сока увеличивать не следует, так как это не дефицитный ресурс.

Найдем интервал изменения каждого активного ограничения, в пределах которого его оценка целевой функции не меняется.

Интервал устойчивости найденной оценки ресурса R1, запаса сырья спелых помидоров в фунтах:

,

.

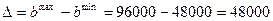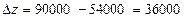Интервал для R1 [48000,96000], оценка 36000/48000=0.75

Интервал устойчивости найденной оценки ресурса R3, количества мест на складе для хранения пасты:

.

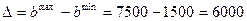
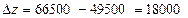Интервал для R1 [1500,7500], оценка 18000/6000=3.

Таким образом, основные направления анализа решения на чувствительность включают исследования возможности изменения запасов ресурсов и коэффициентов целевой функции, выявление приоритетных ресурсов путем определения «ценности» дополнительной единицы ресурсов.

Анализ полученного оптимального решения задачи линейного программирования при заданных ограничениях позволяет в первом приближении «поработать» с полученным решением, попытаться его улучшить.

Симплекс-метод

В реальных задачах линейного программирования количество управляемых переменных значительно больше двух, количество ограничений также велико и поиск 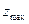простым перебором значений целевой функции 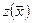во всех вершинах или перемещением соответствующей гиперплоскости даже с использованием компьютера является нерациональным. На практике для решения ЗЛП используются различные модификации симплекс-метода, численный алгоритм которого легко реализуется на компьютере.

Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, определяемого системой неравенств 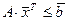, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по любому ребру из текущей вершины к соседней вершине не увеличивает значения функционала, считается, что оптимальное значение найдено.

В классическом симплекс-методе по умолчанию предполагается неотрицательность искомых переменных 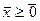и .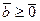

Последовательность вычислений для решения задачи максимизации симплекс-методом можно разделить на две основные фазы:

1) выбор исходной вершины множества допустимых решений;

2) последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда во всех ограничениях 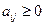(тогда нулевой вектор совершенно точно является допустимым решением, хотя и далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить.

Рассмотрим стандартную задачу линейного программирования в матричном виде:

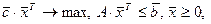
c дополнительными условиями

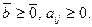
Для применения симплекс-метода задачу нужно записать в каноническом виде:

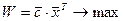
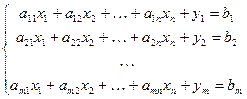(1.17)

.

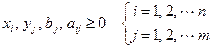Здесь 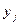— новые переменные, которые вводятся, чтобы все ограничения переписать в виде равенств.

Запишем задачу для удобства в матричном виде:

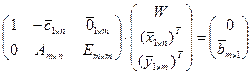. (1.18)

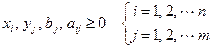
Здесь:

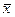— управляемые переменные исходной задачи (1.17),

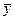— новые переменные, дополняющие старые таким образом, что неравенство 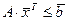переходит в равенство,

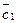— коэффициенты исходной линейной целевой функции,

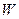— переменная, которую необходимо максимизировать.

Разница между числом переменных 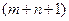и уравнений 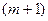даёт нам число степеней свободы 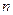. Тогда мы можем присвоить этому числу переменных какие-то значения и назвать их свободными. Остальные переменные при этом будут вычисляться однозначно, и называться базисными. В нашем случае так называемое начальное допустимое решение (вершина, из которой мы начнём движение) очевидно, 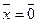. Будем считать 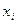свободными переменными, все новые переменные будем считать базисными. При этом значения базовых переменных 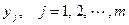вычисляются однозначно: .

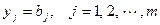Приведём шаги алгоритма. На каждом шаге мы будем двигаться по какому-то ребру к новой вершине. Одна из свободных переменных станет базисной, одна из базисных станет свободной, и система (2) перейдёт в систему

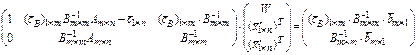
где

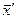— базисные переменные начального или предыдущего шага;

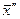— свободные переменные начального или предыдущего шага;

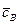— коэффициенты вектора 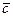, соответствующие базисным переменным в том случае, когда на очередном шаге некоторые из первоначально свободных переменных 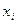переместятся в базисные (переменным 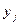всегда соответствует );

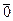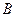— столбцы матрицы 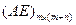, соответствующие базисным переменным.

Матрицу, образованную оставшимися в 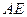столбцами обозначим .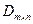