Вычисление по Тьюрингу функций
Рассмотрим расширенный натуральный ряд: 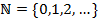 , рассмотрим функции от
, рассмотрим функции от 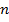 переменных
переменных 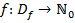 , где
, где 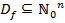
Такие функции называются частичными функциями счётнозначной логики. Множество функций 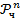 .
.
Если область определения функции совпадает со всем 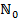 , то тогда
, то тогда 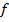 называется всюду определенной.
называется всюду определенной.
Пусть 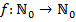 ,
, 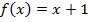 ; закодируем числа натурального ряда:
; закодируем числа натурального ряда: 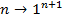 , тогда слово
, тогда слово 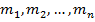 будем записывать на ленте
будем записывать на ленте
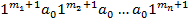
Определение: говорят, что функция 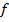 вычислима по Тьюрингу, если существует машина Тьюринга, работающая в алфавите
вычислима по Тьюрингу, если существует машина Тьюринга, работающая в алфавите 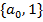 и обладающая следующими свойствами:
и обладающая следующими свойствами:
1. Если набор 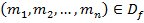 - область определения и
- область определения и  , то машина Тьюринга применима к слову в начальной конфигурации
, то машина Тьюринга применима к слову в начальной конфигурации 
2. Если 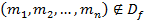 , то машина не применима к слову в начальной конфигурации, то есть начиная работу над словом она начинает циклить.
, то машина не применима к слову в начальной конфигурации, то есть начиная работу над словом она начинает циклить.
Рекурсивные функции:
1. 0 – функция: 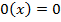
2. Функция следования 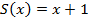
3. Оператор проектирования 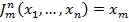
Введем следующие операции:
1. Операция суперпозиции:
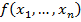
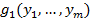
…
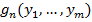
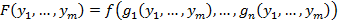
2. Примитивная рекурсия
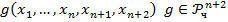
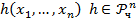
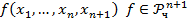
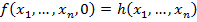
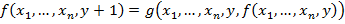
3. Процедура взятия 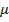 оператора
оператора
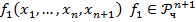
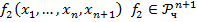
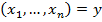
Ищем следующим образом:
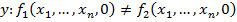
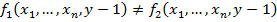
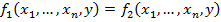

Определение: функция называется частично рекурсивной, если она может быть получена из простейших функций: 0 – функции, функции следования, функции выбора переменной, с помощью конечного числа применений суперпозиций примитивной рекурсии и взятия 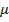 оператора. Если функция всюду определена и частична рекурсивна, она называется общерекурсивной функцией.
оператора. Если функция всюду определена и частична рекурсивна, она называется общерекурсивной функцией.
Теорема: всякая частично рекурсивная функция вычислима по Тьюрингу и наоборот: всякая вычислимая по Тьюрингу функция является частично рекурсивной.
Определение: множество называется общерекурсивным, если оно совпадает с множеством значений некоторой общерекурсивной функции (например множество чётных чисел).
Определение: рассмотрим некоторое множество 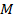 , которое является подмножеством некоторого множества, тогда характеристической функцией данного множества
, которое является подмножеством некоторого множества, тогда характеристической функцией данного множества 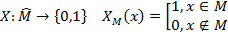
Определение: множество 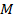 называется рекурсивным, если его характеристическая функция частично рекурсивная.
называется рекурсивным, если его характеристическая функция частично рекурсивная.
Теорема: всякое рекурсивное множество является общерекурсивным.
Нормальные алгоритмы Маркова.
Рассмотрим некоторую совокупность символов – алфавит 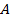 ,
, 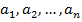 - слово,
- слово, 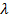 – пустое слово.
– пустое слово.
Определение: Марковской подстановкой называется операция, которая записывается 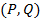 , которая ищет первое вхождение слова
, которая ищет первое вхождение слова 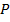 в некоторое слово
в некоторое слово  и заменяет слово
и заменяет слово 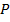 на слово
на слово 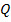 .
.
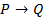 – если дальше продолжаем работу
– если дальше продолжаем работу
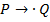 – окончание работы после
– окончание работы после
Работа алгоритма происходит следующим образом: рассматривается слово 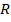 и ищется первое
и ищется первое 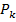 , если ни одно из
, если ни одно из 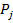 не является подсловом
не является подсловом 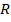 , то в этом случае алгоритм не начинает свою работу, иначе
, то в этом случае алгоритм не начинает свою работу, иначе 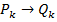 и получаем новое слово
и получаем новое слово 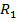 . Если эта подстановка была заключительной, то останавливаемся и результат
. Если эта подстановка была заключительной, то останавливаемся и результат 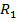 , иначе начинаем работу сначала, но уже с
, иначе начинаем работу сначала, но уже с 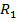 .
.
Определение: функция, заданная на некотором множестве слов алфавита 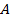 называется нормально вычислимой, если существует такое расширение данного алфавита
называется нормально вычислимой, если существует такое расширение данного алфавита 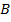 и такой нормальный алгоритм Маркова, работающий над словами алфавита
и такой нормальный алгоритм Маркова, работающий над словами алфавита 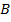 , который каждое слово
, который каждое слово 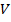 из области определения функции
из области определения функции 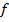 преобразует слово в
преобразует слово в 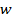 , такое, что
, такое, что 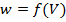 .
.
Принципы нормализации алгоритма Маркова:
Для нахождения значений функции в некотором алфавите тогда и только тогда существует алгоритм, когда функция нормально вычислима.
Теорема: следующие классы функций (заданы на расширенном натуральном ряде и принимают значения с расширенного натурального ряда) совпадают:
1. Класс функций, вычислимых по Тьюрингу
2. Класс частично рекурсивных функций
3. Класс нормально вычислимых функций
Неразрешимые алгоритмические проблемы:
1. Проблема распознавания выводимости в математической логике: для любых двух формул 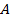 и
и 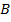 в логическом исчислении узнать, существует ли дедуктивная цепочка, ведущая от формулы
в логическом исчислении узнать, существует ли дедуктивная цепочка, ведущая от формулы 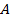 к формуле
к формуле 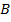
Теорема Чёрча: проблема распознавания выводимости алгоритмически не разрешима.
2. Проблема распознавания самоприменимости.
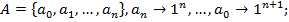
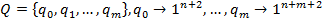
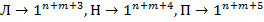
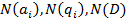 – код символа.
– код символа.
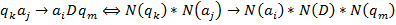
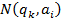 - код команды.
- код команды.
Тогда наша программа – совокупность команд 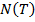
На вход машины Тьюринга Т отправляем 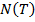
1) если машина Тьюринга применима к своему коду – самопримаенимая
2) если начиная работу над своим кодом машина Тьюринга циклит – несамоприменимая
Таким образом все машины Тьюринга, работающие в алфавите 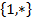 делятся на 2 класса: самоприменимые и несамоприменимые.
делятся на 2 класса: самоприменимые и несамоприменимые.
Проблема самоприменимости состоит в следующем: построить такой алгоритм, который по коду машины Тьюринга Т давал бы однозначный ответ самоприменима машина Т или нет (без запуска).
Для решения проблемы необходимо построить машину 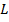 в алфавите
в алфавите 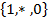 , которая, работая над кодом машины Тьюринга Т, останавливалась и выдавала 1, самоприменима, или 0.
, которая, работая над кодом машины Тьюринга Т, останавливалась и выдавала 1, самоприменима, или 0.
Теорема: проблема самоприменимости алгоритмически не разрешена.
Доказательство: предположим противное: пусть существует машина 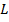 , решающая проблему самоприменимости. Опираясь на неё, построим машину Тьюринга
, решающая проблему самоприменимости. Опираясь на неё, построим машину Тьюринга 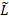 , которая:
, которая:
1) применима к кодам несамоприменимых машин Тьюринга,
2) не применима к кодам самоприменимых машин Тьюринга.
Для этого:
1) все команды машины 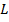 объявляем командами машины
объявляем командами машины 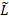 ;
;
2) заключительное состояние 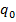 машины
машины 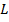 объявляем не заключительным для машины
объявляем не заключительным для машины 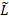 ;
;
3) добавляем заключительное состояние 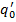 для
для 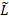 и команды:
и команды:
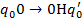
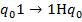
Машина 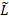 работает над кодами всех машин, в том числе и на своим.
работает над кодами всех машин, в том числе и на своим.
Пусть
1) машина Тьюринга 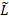 самоприменима, то есть применима к своему коду, но она не применима к кодам самоприменимых машин, значит является несамоприменимой.
самоприменима, то есть применима к своему коду, но она не применима к кодам самоприменимых машин, значит является несамоприменимой.
Получено противоречие.
2) машина Тьюринга 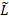 несамоприменима, но она применима к кодам несамоприменимых машин, значит самоприменима.
несамоприменима, но она применима к кодам несамоприменимых машин, значит самоприменима.
Получено противоречие.
3. Проблема применимости.
Машина Тьюринга работает в алфавите 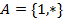 ,
, 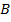 - слово. Требуется по коду машины Тьюринга Т и слову
- слово. Требуется по коду машины Тьюринга Т и слову 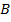 определить, применима ли машина Тьюринга к слову
определить, применима ли машина Тьюринга к слову 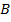 или нет. В разработке такого алгоритма и заключается проблема применимости: построить машину Тьюринга
или нет. В разработке такого алгоритма и заключается проблема применимости: построить машину Тьюринга 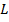 , на вход которой поступает
, на вход которой поступает 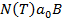 . В результате 1, если машина применима, иначе 0.
. В результате 1, если машина применима, иначе 0.
Теорема: проблема применимости алгоритмически неразрешима.
Доказательство: предположим противное: пусть машину Тьюринга 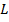 можно построить, тогда наш код - это машина
можно построить, тогда наш код - это машина 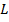 . Подадим слово
. Подадим слово 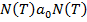 , тогда машина
, тогда машина 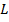 решала бы проблему самоприменимости, а она алгоритмически неразрешима.
решала бы проблему самоприменимости, а она алгоритмически неразрешима.
4. Проблема определения общей рекурсивности алгоримов, т.е. проблема определения того, ко всяким ли допустимым в начале данным применим данный алгоритм.
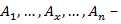 алгоритм. Нужно построить
алгоритм. Нужно построить 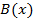 , на вход которой бы поступал номер алгоритма
, на вход которой бы поступал номер алгоритма 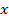 . В результате: 1 – алгоритм всюду определён, 0 – алгоритм
. В результате: 1 – алгоритм всюду определён, 0 – алгоритм 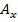 не является общим.
не является общим.
Лемма: для любого перечисления любого множества 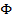 общерекурсивных функций существует функция, не входящая в это перечисление.
общерекурсивных функций существует функция, не входящая в это перечисление.
Доказательство: рассмотрим все общерекурсивные функции 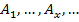 и функцию
и функцию 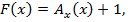
𝐹 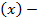 общерекурсивная.
общерекурсивная.
Будем предполагать, что 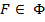 , тогда
, тогда  в нашем перечислении имеет номер
в нашем перечислении имеет номер 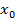 , тогда
, тогда  совпадает с
совпадает с 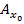 , но
, но 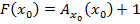 . Получено противоречие.
. Получено противоречие.
Теорема: проблема определения общерекурсивных функций алгоритмически неразрешима.
Доказательство: предположим противное: пусть алгоритм 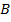 , решающий проблему, существует, тогда он определяет общерекурсивную функцию
, решающий проблему, существует, тогда он определяет общерекурсивную функцию  . На основании
. На основании  построим общерекурсивную функцию следующего вида:
построим общерекурсивную функцию следующего вида:
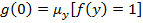
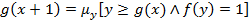
Построенная функция 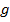 перечисляет все общерекурсивные функции, а так как множество общерекурсивных функций не является счётным, то получили противоречие.
перечисляет все общерекурсивные функции, а так как множество общерекурсивных функций не является счётным, то получили противоречие.
Теория графов.
Основные понятия и определения.
Графом 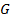 называется пара
называется пара 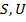 ,
, 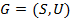 , где
, где 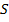 - это множество вершин (в начальном варианте считается конечным и непустым),
- это множество вершин (в начальном варианте считается конечным и непустым), 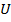 - бинарное отношение, заданное на
- бинарное отношение, заданное на 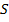 , - множество дуг. Элементы множества
, - множество дуг. Элементы множества 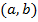 - упорядоченные пары – дуги, где
- упорядоченные пары – дуги, где 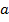 - начало,
- начало, 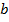 - конец.
- конец.
Вершины, соединённые дугой, называют инцидентными дуге. Между собой – смежными (соединенными одной дугой).
Дуги, имеющие общую вершину, - смежные.
Граф 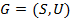 называется ориентированным (орграфом), если
называется ориентированным (орграфом), если 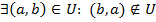
Если 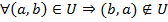 в этом случае граф называют неориентированным (неоргаф).
в этом случае граф называют неориентированным (неоргаф).
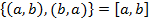 - ребро, без направления.
- ребро, без направления.
Если необходимо представить объекты, связанные несколькими связями, используют мультиграф.
Граф, не содержащий кратных дуг и петель называется простым графом.
Если дугам или вершинам необходимо приписать числа, то речь идёт о взвешенном графе.
Для взвешенного графа 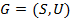 :
:
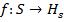 - функция распределения меток вершин,
- функция распределения меток вершин, 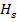 - множество значений;
- множество значений; 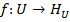 - функция распределения меток дуг,
- функция распределения меток дуг, 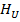 - множество значений.
- множество значений.
Простой граф, в котором каждая пара вершин является смежной, называется полным графом.
Пусть 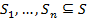 , если
, если 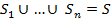 , то тогда это множество подмножеств
, то тогда это множество подмножеств  называется покрытием
называется покрытием 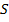 .
.
Граф называется двудольным, если существует такое разбиение множества вершин на два подмножества (доли), что концы каждого ребра принадлежат разным подмножествам (долям), если при этом любые две вершины, входящие в разные дуги, являются смежными, то граф называется полным двудольным графом.
Полный двудольный граф, содержащий в одной доле один элемент – звезда.
Рассмотрим графы 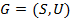 ,
, 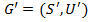 .
.
Графы называются гомоморфными, если существует отображение 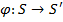 (гомоморфизмом) со свойством:
(гомоморфизмом) со свойством:
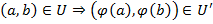
Если 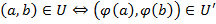 , то
, то 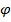 - изоморфизм, а графы
- изоморфизм, а графы 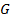 и
и 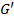 изоморфные.
изоморфные.
