Деформация: относительное растяжение-сжатие, сдвиг

Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.

Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия (другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышаетсяпрочность.

Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно).

Относительная деформация сдвига определяется по формуле: ,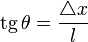

где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов )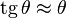

Растяжение - сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, если нагрузка к нему прикладывается по его продольной оси (равнодействующая сил, воздействующих на него, нормальна поперечному сечению стержня и проходит через его центр масс). Рассмотрим прямолинейный стержень постоянного сечения, растягиваемый (сжимаемый) двумя противоположно направленными силами. Используя гипотезу о равномерности распределения напряжений, рассмотрим равновесие некоторой части стержня, отсеченной плоскостью a-a, нормаль которой наклонена к оси стержня под углом α. Внешняя сила F уравновешивается напряжениями, равномерно распределенными по площади наклонного сечения A_α. Обозначив площадь поперечного сечения, перпендикулярную к оси стержня, за A₀, для 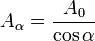. Составив условие равновесия отсеченно части стержня, получим: pA_α−F=0, откуда следует выражение

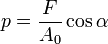
Разложим напряжения p на нормальную σ_α и касательную составляющие.

Коэффициент постели

Гипотеза Фусса — Винклера (или гипотеза коэффициента постели) . Грунт рассматривается как система опирающихся на жесткое горизонтальное основание и не связанных между собой пружин, сжатие которых возрастает прямо пропорционально приложенной нагрузке. Коэффициент пропорциональности между нагрузкой и деформацией называется коэффициентом постели.
Таким образом, сопротивление грунта развивается только непосредственно под нагрузкой и в этом сопротивлении не участвует грунт, расположенный сбоку, который не испытывает осадки.
Основным недостатком данной модели является то, что поверхность грунта, как показывают эксперименты, оседает не только непосредственно под штампом (фундаментом) , но и вокруг него;

Теория местных упругих деформаций Данная теория получила название автора: Фусса-Винклера и была им предложена ещё в 1868 г.

Основная предпосылка этой теории – прямая пропорциональность между давлением и местной осадкой. Основание в данном случае может быть представлено в виде системы пружин не связанных между собой (см. схему). В результате под загруженной балкой пружины будут испытывать сжатие, а за пределами балки – находиться в не сжатом состоянии. 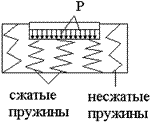Схема модели основания для расчёта гибкой конструкции на упругом основании по методу местных упругих деформаций.

Тогда давление основания под загруженной балкой, может быть определено из следующего выражения: 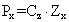, где P_x – давление на подошве фундамента; С_z – коэффициент упругости основания (коэффициент постели); Z_x – упругая осадка грунта в месте приложения нагрузки. Эта модель хорошо отражает работу конструкции, если основание представлено жидкостью. Поэтому чаще всего этот метод используется при строительстве на слабых грунтах или в случае малой мощности слоя сжимаемого грунта.

В последствие было предложено несколько методов, усовершенствующих эту модель; следует отметить наиболее существенные работы авторов: Дутова, Крылова, Кузнецова, Пастернака.

Следует подчеркнуть, что модели соответствующие гипотезе Фусса-Винклера не в состоянии учитывать разновидность оснований (изменение Е_о по глубине и в плане сооружения).

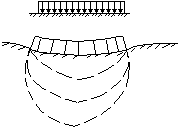
В действительности результаты непосредственных наблюдений показали, что оседает не только нагруженная поверхность, но и соседние участки грунта (см. схему).

Схема деформации основания и гибкой фундаментной балки по результатам эксперимента. Грунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория – общих упругих деформаций.