Тема 1. решение матричных уравнений

КОНТРОЛЬНАЯ РАБОТА №1

Задача 1 связана с действиями над матрицами. Для решения этой задачи следует использовать следующие сведения.

Система 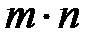чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется матрицей размера 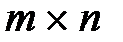и записывается в виде:

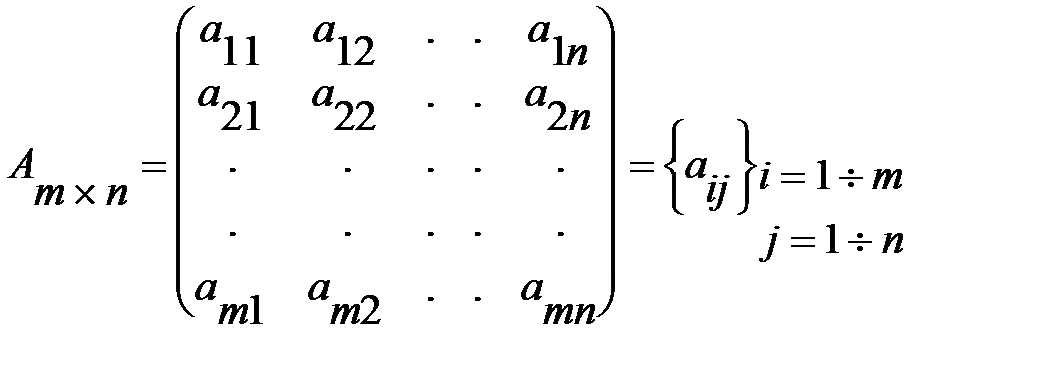
Матрица размера 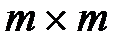называется квадратной матрицей порядка m. Диагональ квадратной матрицы, идущая от левого верхнего угла к правому нижнему, называется главной диагональю, а вторая диагональ называется побочной.

Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные цифры нули, называется единичной матрицей и обозначается следующим образом:

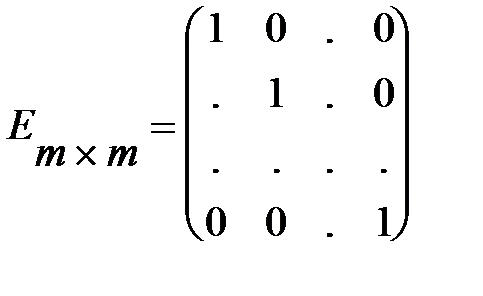
Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах.

Произведением матрицы на число 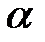называется матрица, каждый элемент которой равен произведению соответствующего элемента матрицы на число .

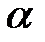Суммой двух матриц одной размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов двух матриц.

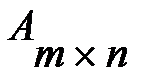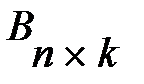Пусть даны две матрицы и , таких что число столбцов матрицы А равно числу строк матрицы В . Тогда произведением матриц 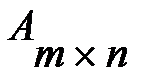и 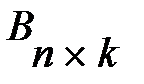называется матрица 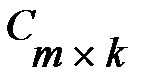,каждый элемент которой C_ij равен сумме попарных произведений элементов i-той строки матрицы А на соответствующие элементы j-того столбца матрицы В, т.е.

Сij = ai1 b1j + ai2 b2j +ai3 b3j +...+ain bnj i = 1… m, j = 1… к.

Заметим, что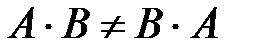

Каждой квадратной матрице ставится в соответствие число

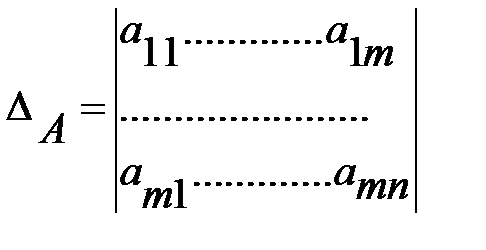
называемое определителем данной матрицы.

Рассмотрим определители для матриц первого, второго и третьего порядков.

а) Пусть А = (а₁₁), тогда 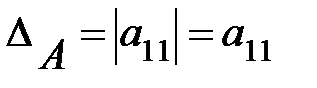. (1)

Из формулы (1) следует, что для матрицы первого порядка определитель совпадает с элементом а₁₁ этой матрицы.

б) Пусть 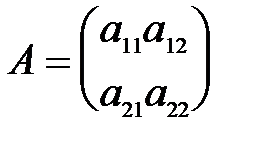, тогда 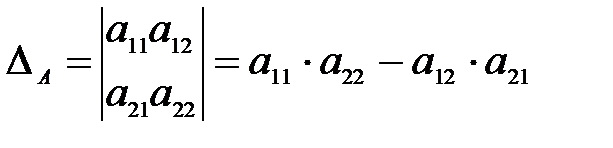. (2)

Из формулы (2) следует, что определитель для матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.

в) Пусть 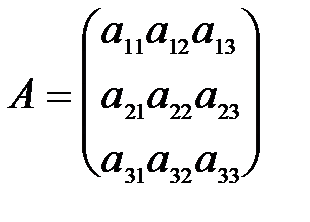, тогда 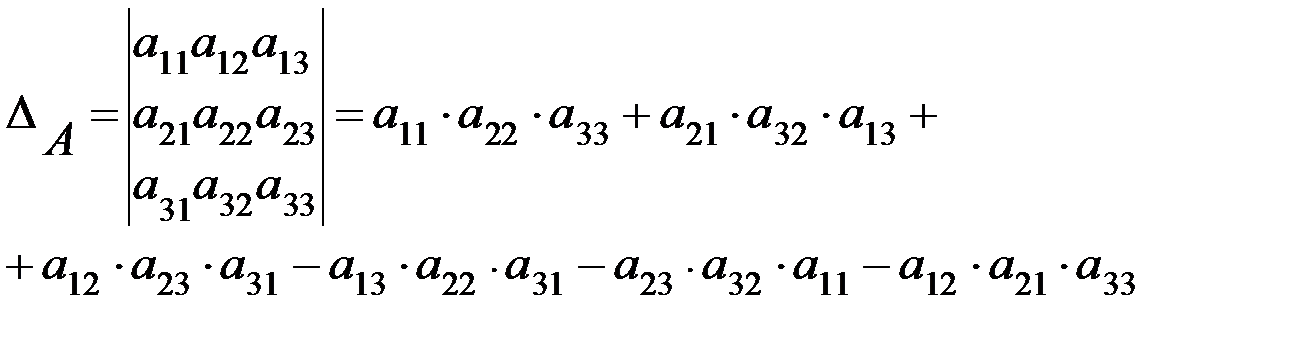(3)

Для удобства запоминания формулы (3) можно использовать «правило треугольников», которое условно показано на схемах 1 и 2 .

схема 1 схема 2

Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1 , а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2 .

Алгебраическим дополнением элемента а_ij квадратной матрицы называется число А_ij , вычисляемое по формуле:

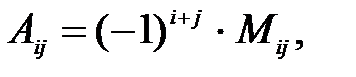где M_ij –определитель, полученный из определителя матрицы 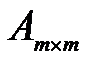удалением строки с номером i и столбца с номером j .

Матрица А^-1 называется обратной к матрице А, если

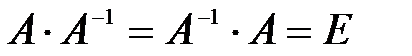, где Е - единичная матрица. Из определения следует, что матрицы А и А^-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от нуля и 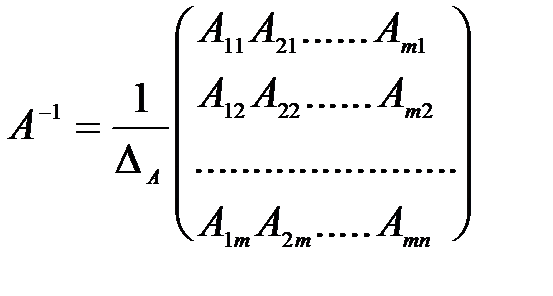, где А_ij -алгебраические дополнения элемента а_ij матрицы .

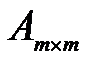Рассмотрим матричное уравнение 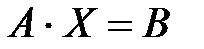, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой не равен . Тогда .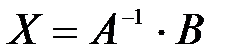

Для уравнения 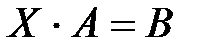, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой не равен нулю, имеем .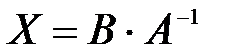