Римеры решения задач к контрольной работе № 2

адача 1.

Доверительным называют такой интервал, который с заданной надежностью γ покрывает оцениваемый параметр.

Для оценки математического ожидания a нормально распределенной случайной величины по выборочной средней `х при неизвестном σ служит доверительный интервал `х - 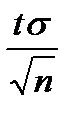< а<`x +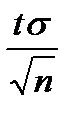

где t – такое значение аргумента функции Лапласа Ф(х) (см. приложение 1), при котором Ф(t) = 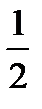γ

Под математическим ожиданием результатов измерений обычно понимают истинное значение измеряемой величины. Поэтому, если, например, в результате 25 измерений среднее арифметическое результатов измерений`х оказалось равным 42,5 м, то для получения доверительного интервала, покрывающего истинное значение измеряемой величины с надежностью g = 0,95, остается указать лишь s, характеризующее точность используемых при измерении приборов.

Пусть s = 2,1. Тогда по таблицам функции Лапласа находим t из равенства Ф(t) = 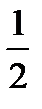× 0,95 = 0,475

Получаем t = 1,96. Отсюда доверительный интервал имеет вид 42,5 - 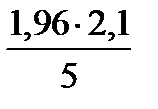< а < 42,5+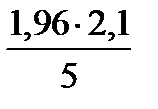

или 41,7 < a < 43,3

адача 2.

Задана выборка значений признака Х, имеющего нормальное распределение:

х₁ -2 1 2 3 4 5

n ₁ 2 1 2 2 2 1

Требуется: а) найти выборочную среднюю`х и исправленное среднее квадратическое отклонение s; б) указать доверительный интервал, покрывающий с надежностью 0,95 неизвестное математическое ожидание а признака Х; в) указать доверительный интервал, покрывающий с надежностью 0,95 среднее квадратическое отклонение s признака Х.

ешение.

а) вычисляем объем выборки: n = ån_i = 2+1+2+2+2+1=10

Тогда `х = 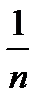ån_ix_i = 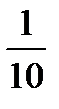[ -2 × 2 + 1 × 1 + 2 × 2 + 3 × 2 + 4 × 2 + 5 × 1] =2

s² = 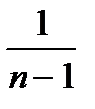ån_i(x_i -x)² = 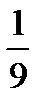[(-2–2)² ×2+(1–2)² ×1+(2–2)² ×2+(3–2)² ×2+(4–2)² ×2+(5–2)² ×1]=5,76; s = 2,4.

б) Искомый доверительный интервал для математического ожидания а имеет вид

`х - t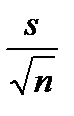<sub>g</sub> < а <`x + t_g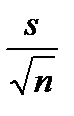

где t_g находим по таблице приложения 2. При g = 0,95 и n = 10 получаем t_g = 2,26. Тогда

`х - t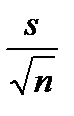<sub>g</sub> = 2 – 2,26 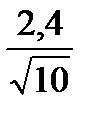= 0,3 `х + t_g 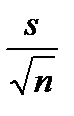= 2 + 2,26 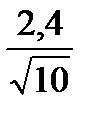= 3,7

Таким образом, 0,3 < a < 3,7

в) доверительный интервал для генерального среднего квадратического отклонения s имеет вид

s (1 – q) < s < s(1+q), если q<1 и

0< s < s(1+q), если q ³ 1

Соответствующие значения q указаны в таблице приложения 3. По заданным g=0,95 и n=10 находим q=0,65. Теперь искомый доверительный интервал запишем следующим образом: s(1–0,65)<s<s(1+0,65)

или 0,84 < s < 3,96

адача 3.

В ходе простого случайного бесповторного опроса 29 студентов получены следующие результаты:

Рост (Х, см)
Число студентов (ni)

1. Найдем размах варьирования:

R=х_тах-х_min; R=170-160=10

2. Размах варьирования R разобьем на k частичных интервалов.

Число k ≈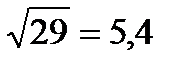

Длина частичного интервала l= R/ k=10/5=2

3. Составим статистическое распределение частот интервального вариационного ряда признака Х:

xi≤x<xi+1	(160-162)	(162- 164)	(164-166)	(166-168)	(168-170)
mi

4. Вычислим:

а) плотность частоты m_i/h каждого интервала:

xi≤x<xi+1	(160-162)	(162- 164)	(164-166)	(166-168)	(168-170)
mi/h					2,5

б) относительные частоты W_i=m_i/n и плотности частот W_i/ h.

xi≤x<xi+1	(160-162)	(162- 164)	(164-166)	(166-168)	(168-170)
Wi=mi/п	0,14	0,28	0,21	0,21	0,16

xi≤x<xi+1	(160-162)	(162- 164)	(164-166)	(166-168)	(168-170)
Wi/ h	0,07	0,14	0,105	0,105	0,08

5. Составим таблицу:

Номер интервала (i)	Частичный интервал xi≤x<xi+1	Сумма частот вариант интервала (mi)	Плотность частоты (mi/h)	Плотность относительной частоты (Wi/ h.)
	(160-162)			0,07
	(162- 164)			0,14
	(164-166)			0,105
	(166-168)			0,105
	(166-168)		2,5	0,08

6. Построим гистограмму частот и гистограмму относительных частот:

Площадь фигуры можно найти, суммируя площади столбцов, являющихся прямоугольниками со сторонами h=2 и m_i /h:

2·2+2·4+2·3+2·3+2·2,5=29 = объем выборки

Площадь фигуры можно найти, суммируя площади столбцов, являющихся прямоугольниками со сторонами h=2 и W_i/ h.:

2·0,07+2·0,14+2·0,105+2·0,105+2·0,08=1

7. Составим статистическое распределение частот дискретного вариационного ряда:

xi, см
mi, чел.

Найдем среднее арифметическое и среднее квадратическое отклонение рассматриваемого признака Х:

Выборочную среднюю 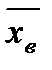найдем по формуле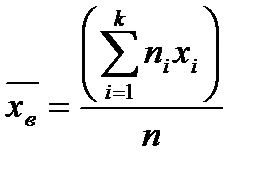

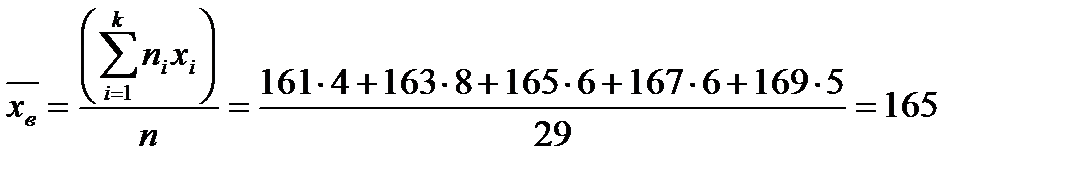
Найдем выборочную дисперсию:

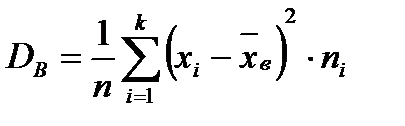
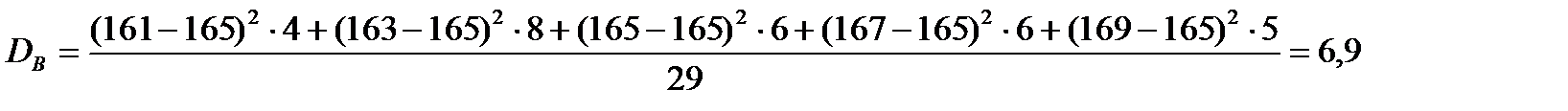
Среднее квадратическое отклонение равно: = ; =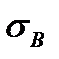

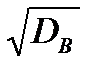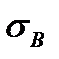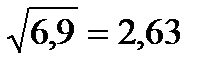
адача 4.

В результате выборочного обследования получено распределение времени на выполнение технологической операции (Х, с) 20 рабочими:

Х	25-30	30-35	35-40	40-45	45-50
Число рабочих

Вычислить выборочные среднюю, моду. медиану, дисперсию. среднее квадратическое отклонение, коэффициент вариации

Решение:

Так как нам задан интервальный ряд, то найдем середины интервалов и примем их в качестве вариант, таким образом, получим дискретный ряд:

Х	27,5	32,5	37,5	42,5	47,5
Число рабочих

Признак Х – время на выполнение технологической операции. Для расчета выборочных характеристик данного распределения составим таблицу:

Х (хi, , с)		число рабочих (тi)		хi,· тi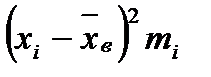
27,5 32,5 37,5 42,5 47,5				82,5 127,5		204,1875 84,5 12,25 136,6875 276,125
Итого						713,75

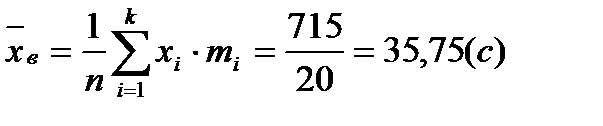- среднее время для выполнения технологической операции.

найдем среднее квадратическое отклонение, для чего найдем дисперсию:

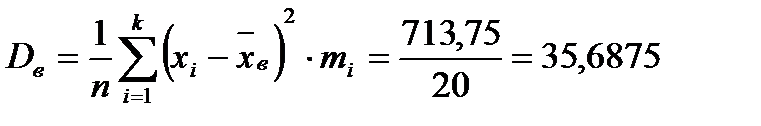
среднее квадратическое отклонение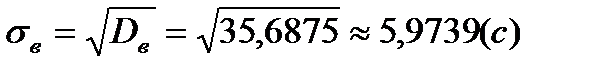

(отклонение от среднего времени выполнения технологической операции составляет 6 сек.).

Коэффициент вариации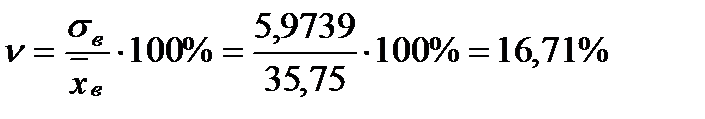

Объем выборки п=20 – число четное. Пусть п=2j,тогда j=10

х_ме=(x_j+x_j+1)/2=(х₁₀+х₁₁)/2=(37,5+37,5)/2=37,5(с)

Кроме того, так как ряд дискретный и число членов нечетно, то медиана равна серединной варианте, то есть х_ме=37,5

Частота достигает максисума: т_i= т_тах=8 при х_i, =32,5, поэтому мода х_мо=32,5(с)

адача 5.

В результате обследования получено выборочное распределение времени, затрачиваемое операторами бухгалтерских машин на обработку документов складского учета (Х – время, с; 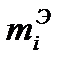- эмпирические частоты(количество документов); 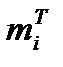- теоретические частоты, вычисленные в предположении о нормальном законе распределения):

хi

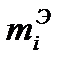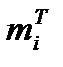Используя критерий Пирсона, при α=0,05 проверить, согласуется ли гипотеза о нормальном распределении признака Х генеральной совокупности с эмпирическим распределением выборки.

Решение:

Выдвигаем нулевую гипотезу Н₀ и ей конкурирующую Н₁.

Н₀: признак Х имеет нормальный закон распределения.

Н₁: признак Х имеет закон распределения, отличный от нормального.

Рассмотрим правостороннюю критическую область. Проверим гипотезу с помощью случайной величины 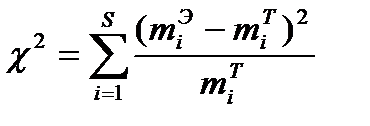, которая имеет распределение χ² с k=s-3=6-3=3 степенями свободы. Вычислим наблюдаемое значение критерия χ²по выборочным данным, представив расчеты в таблице:

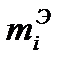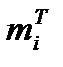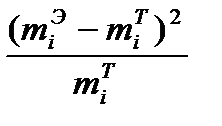			0,167
			2,273
			2,45
			0,059
			0,4
Итого			7,348

Итак 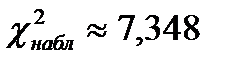. По приложению 4 методического пособия находим критическое значение 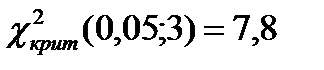. Сравниваем 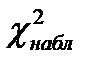и .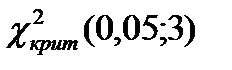

Так как 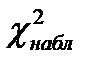< 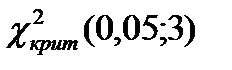, то есть наблюдаемое значение критерия не попало в критическую область, поэтому нулевая гипотеза принимается (справедлива), а конкурирующая отвергается, то есть признак Х имеет нормальный закон распределения, расхождение между теоретическими и эмпирическими частотами незначительно.

адача 6.

Представлены данные, отражающие статистическую связь издержек обращения (Y, тыс. руб.) и товарооборота(Х тыс. руб.):

X	5,0	5,2	5,8	6,4	6,6	7,0
Y	17,6	17,5	18,0	18,1	18,2	18,5

При α=0,1 проверить значимость указанной статистической связи. Построить уравнение регрессии, объяснить его. Спрогнозировать издержки обращения при заданном товарообороте в 17,9 тыс. руб.

Решение:

Признак Х – товарооборот, тыс.руб. (факторный признак). Признак Y – издержки обращения, тыс. руб. (результативный признак). Предполагаем, что признаки имеют нормальный закон распределения. Признаки находятся в статистической зависимости, так как издержки обращения зависят не только от товарооборота, но и от многих других факторов, которые в данном случае не учитываются. Определим форму связи. Построим точки с координатами (x_i; y_i) и по их расположению определим форму связи:

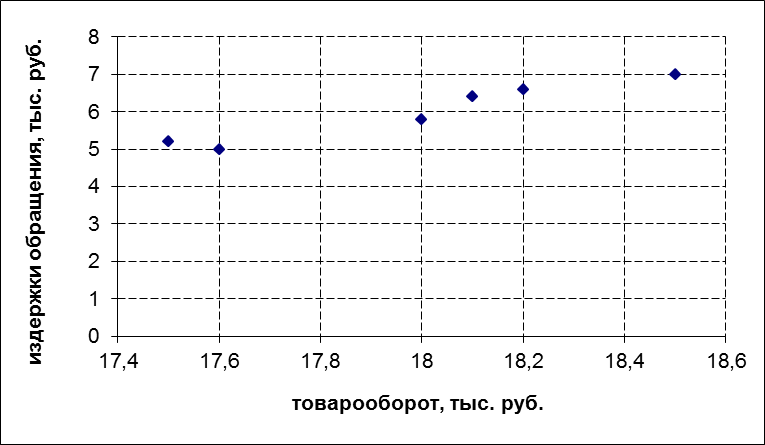
Форма связи: прямая линейная зависимость.

Проведем корреляционный анализ. Вычислим выборочный линейный коэффициент корреляции:

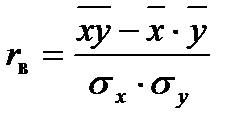
Расчеты представим в таблице:

	xi	yi	xi ·yi·	xi2	yi2
	17,6 17,5 18,1 18,2 18,5	5,2 5,8 6,4 6,6	104,4 115,84 120,12 129,5	309,76 306,25 327,61 331,24 342,25	27,04 33,64 40,96 43,56
Итого	107,98		648,86	1941,11	219,2

;

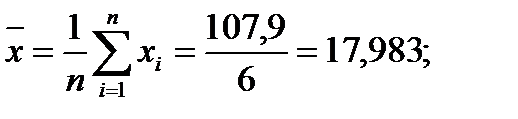
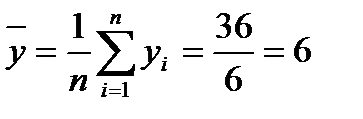
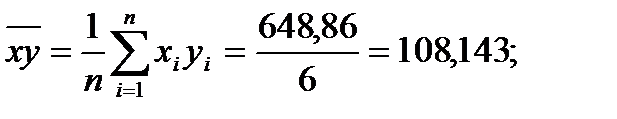
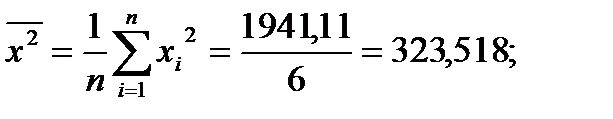
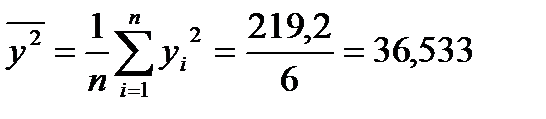
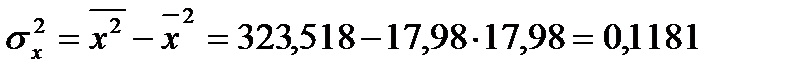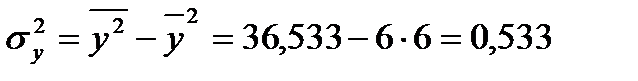
Значит,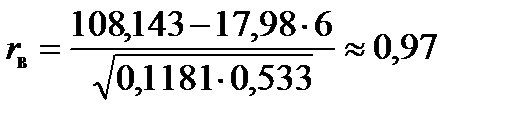

Проверим значимость выборочного коэффициента корреляции. Для этого выдвигаем гипотезы:

Н₀: r_ген=0, Н₁: r_ген≠0

Уровень значимости α=0,1

Для проверки нулевой гипотезы используем случайную величину 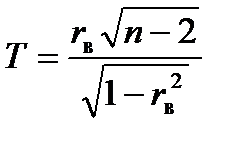имеющую распределение Стьюдента с k= n-2=4 степенями свободы. По выборочным данным найдем наблюдаемое значение критерия:

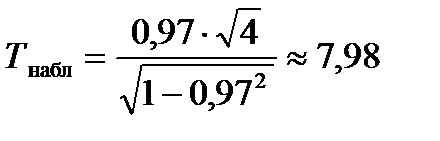
По таблице критических точек распределения Стьюдента определим

t_{крит. дв}(0,1;4)=2,13. Сравниваем 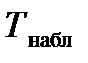и t_крит. (0,1;4). Так как

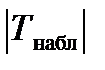> t_{крит. дв}(0,05;3), то есть 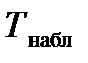попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза: r_ген≠0. Признаки Х и Y коррелированны, 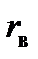значим. Так как 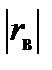близок к единице, следовательно, издержки обращения и товарооборот находятся в тесной корреляционной зависимости.

Найдем коэффициент детерминации. 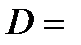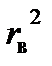·100%=94,09%, то есть вариация

выпуска издержек обращения в среднем на 94,09%объясняется вариацией товарооборота.

Построим уравнение регрессии:

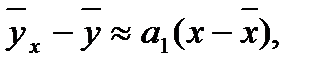
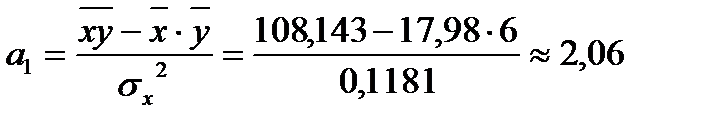
или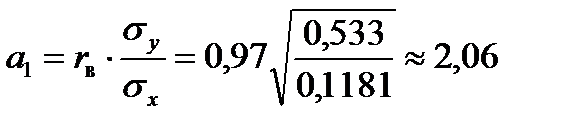

Таким образом, 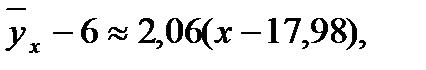или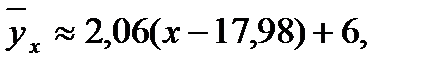

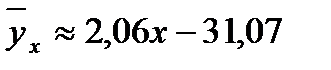из уравнения следует, что с увеличением товарооборота на 1 тыс. руб. издержки обращения увеличиваются на 2,06 тыс.руб.

Найдем по уравнению регрессии издержки обращения, если товарооборот составит 17,9 тыс. руб.:

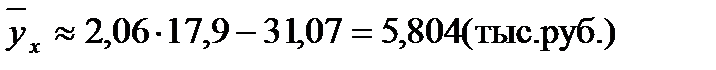
Контрольные вопросы для самоподготовки

Классификация случайных событий.

Классическое определение вероятности.

Основные формулы комбинаторики.

Непосредственный подсчет вероятности.

Относительная частота. Устойчивость относительной частоты.

Статистическая вероятность.

Геометрическая вероятность.

Несовместные и совместные события.

Теорема сложения вероятностей несовместных событий.

Произведение событий.

Понятие условной вероятности.

Теорема умножения вероятностей.

Полная система событий.

Противоположные события.

Соотношения между вероятностями противоположенных событий.

Теорема сложения вероятностей совместных событий.

Формула полной вероятности.

Формула Бейеса.

Повторные независимые испытания.

Формула Бернулли.

Локальная теорема Муавра-Лапласа и условия её применимости.

Асимптотическая формула Пуассона и условия её применимости.

Интегральная теорема Муавра-Лапласа, и условия её применимости.

Следствие из интегральной теоремы Муавра-Лапласа.

Понятие случайной величины.

Дискретная случайная величина и законы ее распределения.

Математическое ожидание дискретной случайной величины и его свойства.

Вероятностный смысл математического ожидания.

Дисперсия дискретной случайной величины и её свойства

Среднее квадратическое отклонение дискретной случайной величины.

Биноминальное распределение вероятностей случайной величины. Числовые характеристики.

Случайная величина распределенная по закону Пуассона, ее числовые характеристики.

Числовые характеристики средней арифметической одинаково распределенных случайных величин.

Частота и частности наступления события в n повторных независимых испытания.

Начальные и центральные теоретические моменты.

Функция распределения случайной величины, ее свойства и график.

Плотность распределения вероятностей непрерывной случайной величины, её свойства и график.

Связь между плотностью вероятностей и функцией распределения.

Числовые характеристики непрерывной случайной величины.

Нормальный закон распределения.

Математическое ожидание и дисперсия нормально распределенной случаной величины.

Функция распределения нормально распределенной случайной величины и ее выражение через функцию Лапласа.

Вывод формул для определения вероятностей P(α<Х<β) и P(|Х-a|≤δ), если Х – нормально распределенная случайная величина.

Функция двух случайных аргументов.

Распределение «хи квадрат».

Распределение Стьюдента.

Распределение F Фишера – Cнедекора.

Понятие о законе больших чисел.

Лемма Чебышева.

Неравенство Чебышева.

Теорема Чебышева.

Теорема Бернулли.

Теорема Ляпунова.

Система двух случайных величин.

Функция распределения двумерной случайной величины, её свойства.

Двумерная плотность вероятности, её свойства.

Цепи Маркова

Задачи математической статистики.

Генеральная и выборочная совокупность.

Повторная, бесповторная, репрезентативная выборка.

Способы отбора.

Статистическое распределение выборки.

Эмпирическая функция распределения.

Полигон и гистограмма.

Статистические оценки параметров распределения.

Несмещенные, эффективные и состоятельные оценки.

Генеральная и выборочная средняя.

Оценка генеральной средней по выборочной средней.

Генеральная и выборочная дисперсия.

Оценка генеральной дисперсии по исправленной выборочной.

Формула вычисления дисперсии.

Групповая, внутригрупповая, межгрупповая и общая дисперсия. Сложение дисперсий.

Точность оценки, доверительная вероятность, доверительный интервал.

Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ.

Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ.

Оценка истинного значения измеряемой величины.

Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения.

Оценка точности измерений.

Что такое статистическая гипотеза?

Ошибки первого и второго рода.

Статистический критерий проверки нулевой гипотезы.

Мощность критерия.

Критическая область. Критические точки.

Распределение Фишера – Снедекора.

Проверка гипотезы о значении генеральной средней.

Проверка гипотезы о равенстве генеральных средних двух нормальных совокупностей.

Проверка гипотезы о значении генеральной дисперсии.

Проверка гипотезы о равенстве дисперсий двух нормальных совокупностей.

Вычисление мощности критерия при проверке гипотезы о значении генеральной средней.

Вычисление мощности критерия при проверке гипотезы о значении генеральной дисперсии.

Проверка гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона.

Сформулируйте две основные задачи корреляции.

Сформулируйте задачи регрессионного анализа.

Какая зависимость между величинами называется корреляционной?

Различия функциональной и корреляционной зависимостей.

В чем состоит сущность метода наименьших квадратов, метода выбранных точек, метода средней для определения линии регрессии.

Виды уравнений регрессии.

Что называется выборочным коэффициентом корреляции?

Сформулируйте основные свойства выборочного коэффициента корреляции.

Исходные предпосылки регрессионного анализа.

Оценки коэффициентов регрессии.

Демонстрационный вариант теста к зачету

1. Вероятность достоверного события равна…

1) 0,5

2) 1,0

3) 0

4) 0,25

2. Монета брошена 10 раз. «Герб» выпал 5 раз. Тогда относительная частота выпадения «герба» равна…

1) 0,5

2) 0,6

3) 0,4

4) 0

3. Бросают игральную кость. Вероятность того, что выпадет четное число очков, равна…

1) 1/2

2) 1/3

3) 1/6

4) 5/6

4. Количество перестановок букв в слове «число» равно…

1) 120

2) 6

3) 720

4) 24

5. Сколько хорд можно провести через 6 точек, лежащих на одной окружности…

1) 15

2) 30

3) 10

4) 20

6. В группе из 9 студентов выбирается староста и заместитель старосты. Сколькими способами можно это сделать…

1) 72

2) 90

3) 100

4) 81

7. В урне 30 шаров: 15 белых, 10 красных, 5 синих. Тогда вероятность вынуть цветной шар, если вынимается один шар, равна…

1) 0,1

2) 0,5

3) 0,2

4) 0,7

8. Имеется два ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 стандартных деталей. Из каждого ящика наудачу вынимаются по одной детали. Тогда вероятность того, что обе вынутые детали окажутся стандартными, равна…

1) 0,1

2) 0,56

3) 0,06

4) 0,6

9. Консультационный пункт института получает пакеты с контрольными работами студентов из города А, В и С. Вероятность получения пакета из города А равна 0,6, из города В - 0,1. Тогда вероятность того, что очередной пакет будет получен из города С, равна…

1) 0,3

2) 0,2

3) 0,1

4) 0,5

10. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…

1) 0,45

2) 0,4

3) 0,55

4) 0,9

11. Вероятность того, что студент сдаст на «отлично» первый экзамен равна 0,5, второй – 0,4. Тогда вероятность того, что студент сдаст на «отлично» оба экзамена, равна…

1) 0,2

2) 0,3

3) 0,15

4) 0,9

12. Два станка производят по одному выстрелу. Вероятность попадания в цель для первого и второго станков равны 0,8 и 0,75 соответственно. Тогда вероятность того, что цель будет поражена, равна…

1) 0,6

2) 0,95

3) 0,55

4) 0,4

13. Если вероятность наступления события А в каждом испытании постоянна, отличном от нуля и единицы, то для нахождения вероятности того, что событие А произойдет к раз в п испытаниях, следует использовать…

1) формулу Бернулли	2) формулу полной вероятности
3) формулу Бейеса	4) теорему умножения вероятностей

14. Если вероятность наступления события А, в каждом испытании постоянна, но мала, а число испытаний велико, и если пр 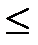10, то для нахождения вероятности того, что событие А произойдет к раз в п испытаниях, следует использовать…

1) формулу Бернулли	2) локальную теорему Муавра-Лапласа
3) формулу Пуассона	4) теорему умножения вероятностей

15. Дискретная случайная величина X имеет закон распределения вероятностей:

Тогда математическое ожидание M(X) этой случайной величины равно…

1) 0,4

2) 1,7

3) 0,8

4) 1,1

16. Математическое ожидание случайной величины Х равно 5. Тогда математическое ожидание случайной величины Y = 2Х+1 равно…

1) 25

2) 21

3) 13

4) 11

17. Дисперсия случайной величины Х равна 2. Тогда дисперсия случайной величины Y = 2Х+1 равна…

1) 4

2) 5

3) 8

4) 9

18. Непрерывная случайная величина Х задана плотностью распределения вероятностей 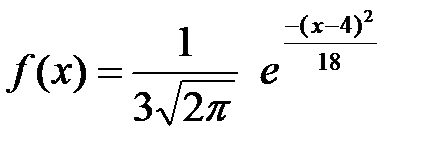. Тогда математическое ожидание этой нормально распределенной случайной величины равно…

1) 4

2) 18

3) 8

4) 2

19. Непрерывная случайная величина задана функцией распределения 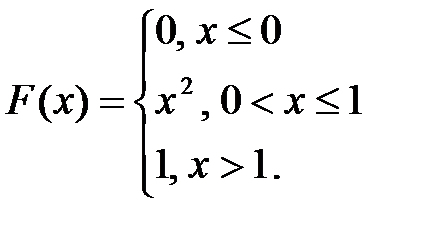. Тогда вероятность того, что случайная величина примет значение в интервале 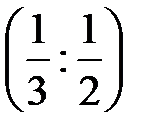равна…

1)

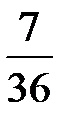2)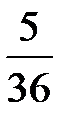

3)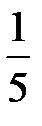

4) 1,0

20. Каким из положений закона больших чисел оценивается вероятность отклонения случайной величины Х от ее математического ожидания…

1) неравенством Чебышева	2) теоремой Бернулли
3) теоремой Чебышева	4) леммой Маркова

ТАБЛИЦЫ

Таблица значений функции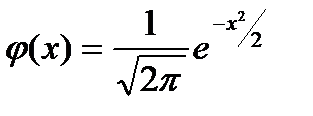

0,0	0,3989
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0,2420
1,1
1,2
1,3
1.4
1,5
1,6
1,7
1,8
1,9
2,0	0,0540
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,0044
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9

Таблица значений функции Φ(х)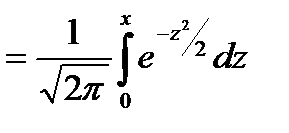

Х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0,00 0,01 0,02 0,03 0,04 0,05	0,0000 0,0040 0,0080 0,0120 0,0160 0,0199	0,40 0,41 0,42 0,43 0,44 0,45	0,1554 0,1591 0,1628 0,1664 0,1700 0,1736	0,80 0,81 0,82 0,83 0,84 0,85	0,2881 0,2910 0,2939 0,2967 0,2995 0,3023	1,20 1,21 1,22 1,23 1,24 1,25	0,3849 0,3869 0,3883 0,3907 0,3925 0,3944
0,06 0,07 0,08 0,09 0,10 0,11	0,0239 0,0279 0,0319 0,0359 0,0398 0,0438	0,46 0,47 0,48 0,49 0,50 0,51	0,1772 0,1808 0,1844 0,1879 0,1915 0,1950	0,86 0,87 0,88 0,89 0,90 0,91	0,3051 0,3078 0,3106 0,3133 0,3159 0,3186	1,26 1,27 1,28 1,29 1,30 1,31	0,3962 0,3980 0,3997 0,4015 0,4032 0,4049
0,12 0,13 0,14 0,15 0,16 0,17	0,0478 0,0517 0,0557 0,0596 0,0636 0,0675	0,52 0,53 0,54 0,55 0,56 0,57	0,1985 0,2019 0,2054 0,2088 0,2123 0,2157	0,92 0,93 0,94 0,95 0,96 0,97	0,3212 0,3238 0,3264 0,3289 0,3315 0,3340	1,32 1,33 1,34 1,35 1,36 1,37	0,4066 0,4082 0,4099 0,4115 0,4131 0,4147
0,18 0,19 0,20 0,21 0,22 0,23	0,0714 0,0753 0,0793 0,0832 0,0871 0,0910	0,58 0,59 0,60 0,61 0,62 0,63	0,2190 0,2224 0,2257 0,2291 0,2324 0,2357	0,98 0,99 1,00 1,01 1,02 1,03	0,3365 0,3389 0,3413 0,3438 0,3461 0,3485	1,38 1,39 1,40 1,41 1,42 1,43	0,4162 0,4177 0,4192 0,4207 0,4222 0,4236
0,24 0,25 0,26 0,27 0,28 0,29	0,0948 0,0987 0,1026 0,1064 0,1103 0,1141	0,64 0,65 0,66 0,67 0,68 0,69	0,2389 0,2422 0,2454 0,2486 0,2517 0,2549	1,04 1,05 1,06 1,07 1,08 1,09	0,3508 0,3531 0,3554 0,3577 0,3599 0,3621	1,44 1,45 1,46 1,47 1,48 1,49	0,4251 0,4265 0,4279 0,4292 0,4306 0,4319
0,30 0,31 0,32 0,33 0,34 0,35	0,1179 0,1217 0,1255 0,1293 0,1331 0,1368	0,70 0,71 0,72 0,73 0,74 0,75	0,2480 0,2611 0,2642 0,2673 0,2703 0,2734	1,10 1,11 1,12 1,13 1,14 1,15	0,3643 0,3665 0,3686 0,3708 0,3729 0,3749	1,50 1,51 1,52 1,53 1,54 1,55	0,4332 0,4345 0,4357 0,4370 0,4382 0,4394
0,36 0,37 0,38 0,39	0,1406 0,1443 0,1480 0,1517	0,76 0,77 0,78 0,79	0,2764 0,2794 0,2823 0,2852	1,16 1,17 1,18 1,19	0,3770 0,3790 0,3810 0,3830	1,56 1,57 1,58 1,59	0,4406 0,4418 0,4429 0,4441

Х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,60 1,61 1,62 1,63 1,64 1,65 1,66	0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515	1,85 1,86 1,87 1,88 1,89 1,90 1,91	0,4678 0,4686 0,4693 0,4690 0,4706 0,4713 0,4719	2,20 2,22 2,24 2,26 2,28 2,30 2,32	0,4861 0,4868 0,4875 0,4881 0,4887 0,4893 0,4898	2,70 2,72 2,74 2,76 2,78 2,80 2,82	0,4965 0,4967 0,4969 0.4971 0,4973 0,4974 0,4976
1,67 1,68 1,69 1,70 1,71 1,72	0,4525 0,4535 0,4545 0,4554 0,4564 0,4573	1,92 1,93 1,94 1,95 1,96 1,97	0,4726 0,4732 0,4748 0,4744 0,4750 0,4756	2,34 2,36 2,38 2,40 2,42 2,44	0,4904 0,4909 0,4913 0,4918 0,4922 0,4927	2,84 2,86 2,88 2,90 2,92 2,94	0,4977 0,4979 0,4980 0,4981 0,4982 0,4984
1,73 1,74 1,75 1,76 1,77 1,78	0,4582 0,4591 0,4599 0,4608 0,4616 0,4625	1,98 1,99 2,00 2,02 2,04 2,06	0,4761 0,4767 0,4772 0,4783 0,4793 0,4803	2,46 2,48 2,50 2,52 2,54 2,56	0,4931 0,4934 0,4938 0,4941 0,4945 0,4948	2,96 2,98 3,00 3,20 3,40 3,60	0,4985 0,4986 0,49865 0,49931 0,49966 0,499841
1,79 1,80 1,81 1,82 1,83 1,84	0,4633 0,4641 0,4649 0,4656 0,4664 0,4671	2,08 2,19 2,12 2,14 2,16 2,18	0,4812 0,4821 0,4830 0,4838 0,4846 0,4854	2,58 2,60 2,62 2,64 2,66 2,68	0,4951 0,4953 0,4956 0,4959 0,4961 0,4963	3,80 4,00 4,50 5,00 ¥	0,499928 0,499968 0,499997 0,49999997 0,5

Таблица значений t_g = t(g, n)

n	g	n	g
	0,95	0,99	0,999		0,95	0,99	0,999
	2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 2,12 2,11 2,10	4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88	8,61 6,86 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92	¥	2,093 2,064 2,045 2,032 2,023 2,016 2,009 2,001 1,996 1,991 1,987 1,984 1,980 1,960	2,861 2,797 2,756 2,720 2,708 2,692 2,679 2,662 2,649 2,640 2,633 2,627 2,617 2,576	3,883 3,745 3,659 3,600 3,558 3,527 3,502 3,464 3,439 3,418 3,403 3,392 3,374 3,391

Таблица значений q =q(g, n)

n	g	n	g
	0,95	0,99	0,999		0,95	0,99	0,999
	1,37 1,09 0,92 0.80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39	2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60	5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92		0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089	0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120	0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162

Критические точки распределения χ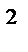

Число степеней свободы k	Уровень значимости α
0,01	0,025	0,05	0,95	0.975	0,99
	6.6	5,0	3,8	0,0039	0.00098	0,00016
	9,2	7,4	6.0	0,103	0.051	0,020
	11,3	9,4	7,8	0.352	0.216	0,115
	13,3	11.1	9.5	0,711	0,484	0,297
	15,1	12,8	11.1	1.15	0,831	0,554
	16,8	14,4	12.6	1,64	1.24	0,872
	18,5	16,0	14.1	2.17	1.69	1,24
	20,1	17,5	15,5	2,73	2.18	1,65
	21,7	19,0	16,9	3,33	2.70	2,09
	23,2	20,5	18,3	3,94	3,25	2,50
	24,7	21.9	19,7	4,57	3,82	3,05
	26,2	23,3	21,0	5,23	4,40	3,57
	27,7	24,7	22,4	5.89	5,01	4,11
	29,1	26,1	23,7	6,57	5,63	4,66
	30,6	27,5	25,0	7,26	6,26	5,23
	32,0	28,8	26,3	7,96	6,91	5,81
	33,4	30,2	27,6	8,67	7,56	6,41
	34,8	31,5	28,9	9,39	8,23	7,01
	36,2	32,9	30,1	10,1	8,91	7,63
	37,6	34.2	31.4	10,9	9,59	8,26
	38,9	35,5	32,7	11,6	10,3	8,90
	40,3	36,8	33,9	12,3	11.0	9,54
	41,6	38.1	35,2	13,1	11,7	10,2
	43,0	39.4	36.4	13.8	12,4	10,9
	44,3	40.6	37,7	14,6	13,1	11,5
	45,6	41,9	38,9	15,4	13,8	12,2
27-	47,0	43,2	40,1	16,2	14,6	12,9
	48,3	44,5	41,3	16,9	15,3	13,6
	49,6	45,7	42,6	17,7	16,0	14,3
	50,9	47,0	43,8	18,5	16,8	15,0

Критические точки распределения Стьюдента