Теоретический материал. 1Методы построения частотных характеристик

1Методы построения частотных характеристик

При рассмотрении и сравнение частотных характеристик амплитудных и фазочастотных для устройств различных видов возникает проблема их компактного представления, так как значения амплитуд и частот (см. рис. 5.1) существенно различаются друг от друга. Кроме того, и сама величина диапазона частот, в котором характеристики конкретного устройства представляют интерес, может быть весьма значительна, от долей герц до десятков мегагерц.

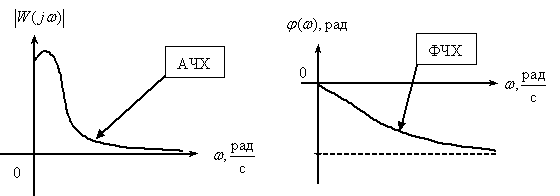
Рис. 5.1

Решение этой проблемы лежит в использовании логарифмических масштабов в частотных характеристиках.

Впервые обратились к логарифмическим масштабам в технике связи, так как там рассматриваются объекты, как с большими коэффициентами усиления, так и объекты которые характеризуются существенным затуханием сигналов.

В технике связи используют понятие коэффициента передачи по мощности для четырехполюсника, показанного на рис. 5.2,

Рис. 5.2

.

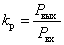Значительный диапазон изменения этого коэффициента и заставил использовать логарифмическое представление, логарифмический коэффициент передачи по мощности –

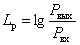(5.1)

Логарифмический коэффициент усиления по мощности измеряют специальными единицами, которые носят название Белл (Б).

1 Белл соответствует усилению мощности в 10 раз.

Чаще используют единицу в десять раз меньшую – децибел (дБ).

.

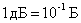При определении логарифмического коэффициента в децибелах, выражение (5.1) принимает вид –

.

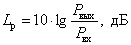Логарифмический коэффициент усиления можно выразить через отношение выходного и входного напряжений при одинаковых нагрузочных сопротивлениях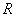

.

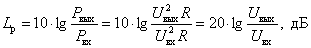Такое представление коэффициента усиления используют в теории автоматического управления для измерения амплитуды частотной характеристики в децибелах –

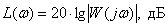(5.2)

По оси частот в теории автоматического управления так же используют логарифмический масштаб на основе десятичного логарифма частоты.

При этом ось частот будет иметь следующий вид –

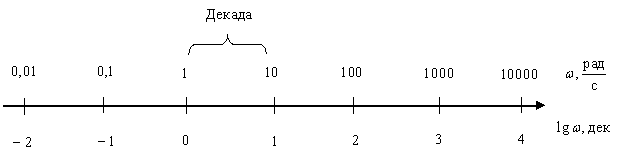
Рис. 5.3

Изменение частоты в десять раз называют декадой. Причем на оси частот, при ее логарифмическом масштабе, принято обозначать значения частоты в рад/с, иногда в герцах, особенно это принято в радиотехнике и в инженерной практике.

Особо отметим, что логарифмическая шкала не имеет нуля и может пересекаться вертикальной осью в любом месте, что особенно важно тем, что дает возможность рассматривать частотные свойства динамических звеньев и конкретных устройств в необходимом диапазоне изменения частот, где характеристика представляет интерес для исследователя.

Теперь дадим определение логарифмическим частотным характеристикам.

Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического звена называют такое представление амплитудной частотной характеристики (АЧХ), в котором модуль (амплитуда) частотной характеристики выражен в децибелах, а частота – в логарифмическом масштабе.

Логарифмической фазовой частотной характеристикой (ЛФЧХ) динамического звена называют такое представление фазочастотной характеристики (ФЧХ) , в котором частота выражена в логарифмическом масштабе.

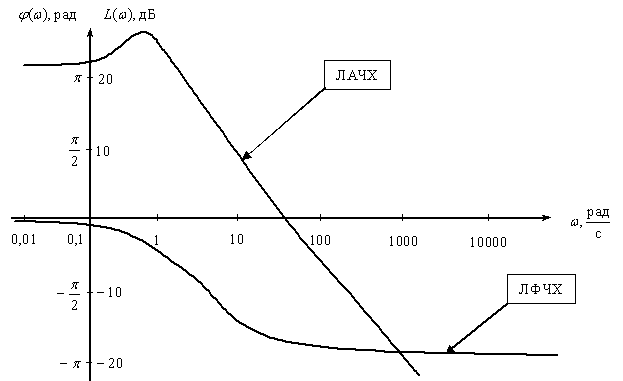
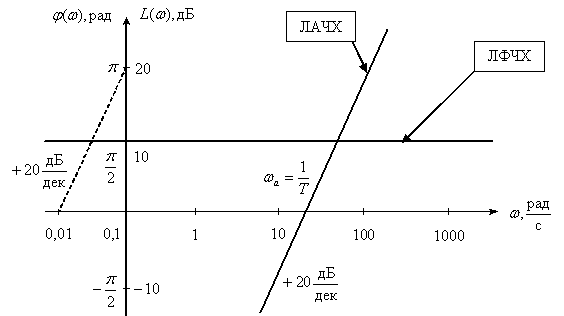
Довольно часто ЛАЧХ И ЛФЧХ строятся на одном графике, чтобы давать полное представление о свойствах объекта, покажем на рис. 4 примерный вид и оформление ЛАЧХ и ЛФЧХ некоторого инерционного объекта.

Логарифмические частотные характеристики элементарных динамических звеньев

Безынерционное звено

Передаточная функция –

.

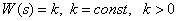Частотная характеристика –

,

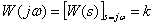АЧХ и ФЧХ

.

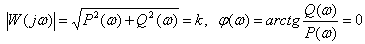Логарифмические характеристики

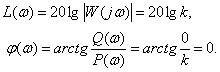
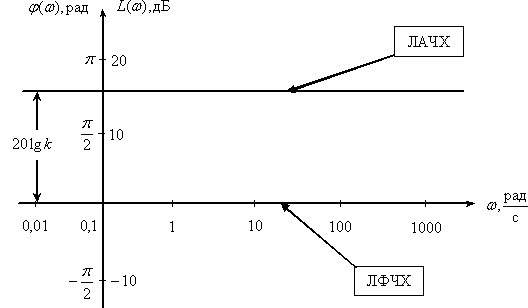
Дифференцирующее звено

Передаточная функция –

.

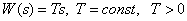Частотная характеристика –

,

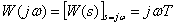АЧХ и ФЧХ

.

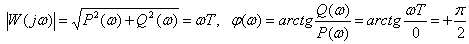Логарифмические характеристики

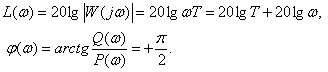
Для удобства построения определим точку, где ЛАЧХ пересекает ось частот –

.

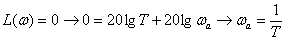Определим наклон ЛАЧХ

,

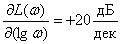то есть, получаем, что ЛАЧХ получает приращение 20 децибел на интервале частот в 1 декаду.

Интегрирующее звено

Передаточная функция –

.

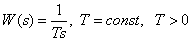Частотная характеристика –

,

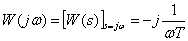АЧХ и ФЧХ

.

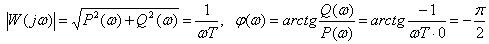Логарифмические характеристики

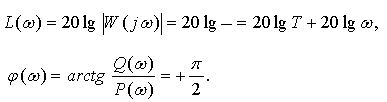
Для удобства построения определим точку, где ЛАЧХ пересекает ось частот –

.

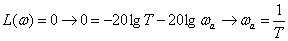Определим наклон ЛАЧХ

,

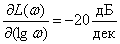то есть, получаем, что ЛАЧХ получает уменьшение на 20 децибел на интервале частот в 1 декаду.

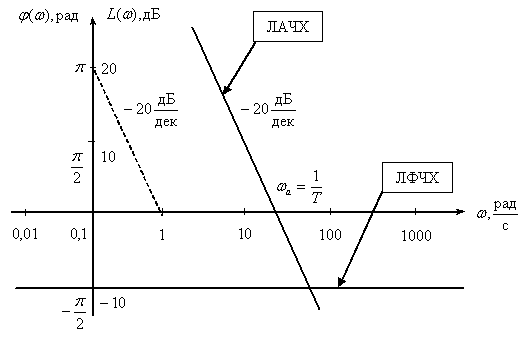
Логарифмические характеристики

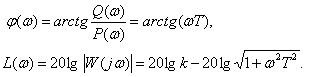
В этом случае, при частоте –

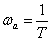
имеем

.

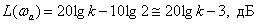Рассмотри для апериодического звена два характерных диапазона:

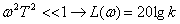(5.3)

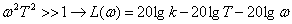(5.4)

,

.

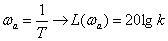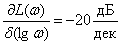Выражения (5.3) и (5.4) представляют собой уравнения прямых линий – асимптот, к которым стремиться ЛАЧХ при удалении от точки их сопряжения 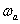. Как мы увидим в дальнейшем, при синтезе и анализе систем бывает удобнее пользоваться не точными, а асимптотическими характеристиками.

Как мы увидели при работе с простейшими типовыми звеньями, частотные характеристики могут быть получены по передаточной функции. В более сложных случаях, при решении задач синтеза и анализа САУ возникает потребность в получении характеристик САУ по известным характеристикам звеньев, входящих в САУ.

Наиболее часто используется случай, когда звенья в САУ включаются последовательно, как это показано на рис. 5.4.

Рис. 5.4

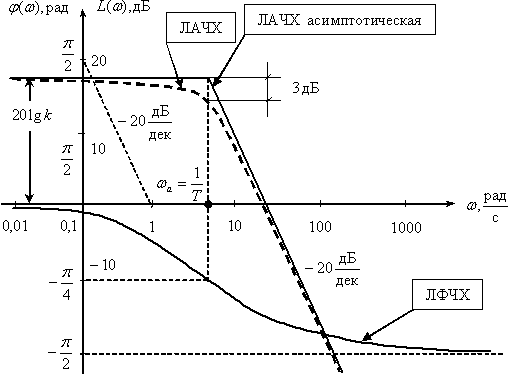
В соответствии с правилами эквивалентных преобразований передаточная функция всей САУ будет иметь вид –

.

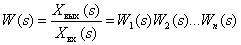Получим частотную характеристику САУ

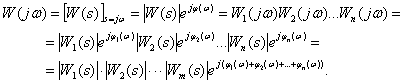
Следовательно,

АЧХ САУ –

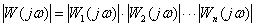(5.5)

ФЧХ САУ

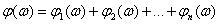(5.6)

Получим по выражениям (5.5) и (5.6) логарифмические характеристики САУ:

ЛАЧХ –

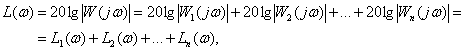(5.7)

ЛФЧХ –

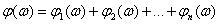(5.8)

Таким образом, логарифмические частотные характеристики САУ могут быть определены, как сумма логарифмических частотных характеристик последовательно включенных составляющих САУ звеньев. Логарифмические масштабы и использование асимптот позволяет осуществить суммирование графически.

В ТАУ так же используются свойства логарифмических частотных характеристик динамических звеньев, передаточные функции которых взаимообратные –

.

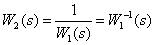Пусть частотные характеристики звена 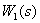известны:

Частотная характеристика –

,

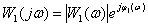ЛАЧХ –

,

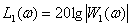ЛФЧХ –

.

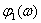Тогда частотные характеристики звена 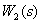имеют вид:

Частотная характеристика –

,

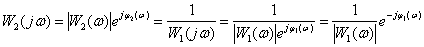ЛАЧХ –

,

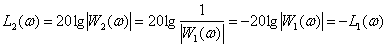ЛФЧХ –

.

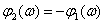Таким образом, ЛАЧХ и ЛФЧХ взаимообратных динамических звеньев расположены симметрично относительно оси частот, подтверждением чему служат полученные ранее ЛАЧХ и ЛФЧХ дифференцирующего и интегрирующего звеньев.

Пример

Для САУ была определена передаточная функция. Следует определить ЛАЧХ САУ.

.

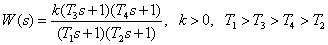Решение

Представим САУ в виде последовательно включенных динамических звеньев

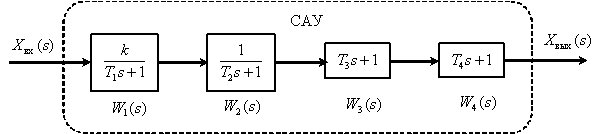
Получим асимптотические ЛАЧХ для каждого апериодического звена

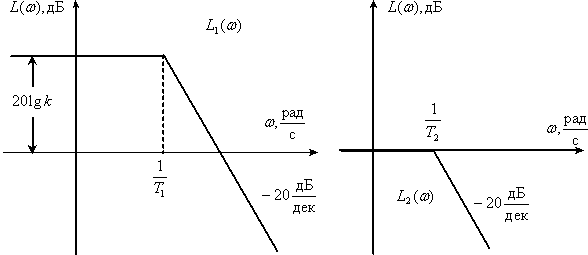
Используя свойства ЛАЧХ взаимообратных звеньев, получим асимптотические ЛПЧХ форсирующих звеньев .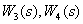

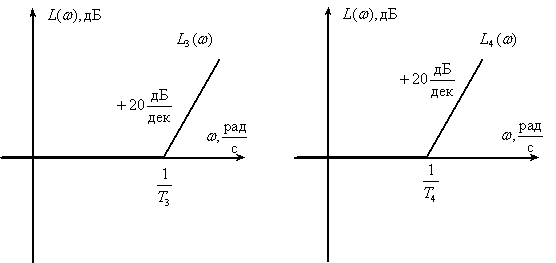
Получим асимптотическую ЛАЧХ САУ выполнив графическое суммирование ЛАЧХ звеньев

.

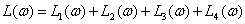Задачу существенно упрощает то, что асимптотические графики звеньев имеют участки с целочисленным наклоном.

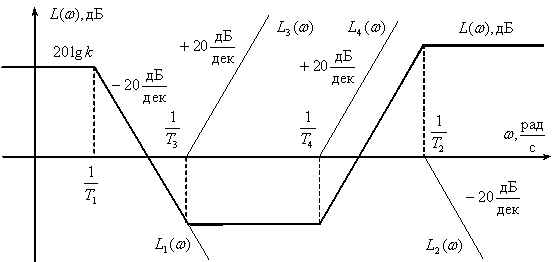
Получим ЛАЧХ и ЛФЧХ типовых звеньев, используя рассмотренное выше.

Реальное дифференцирующее звено

Передаточная функция

.

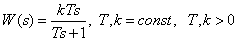Представим звено в следующем виде

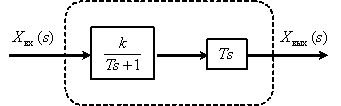
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

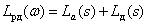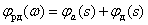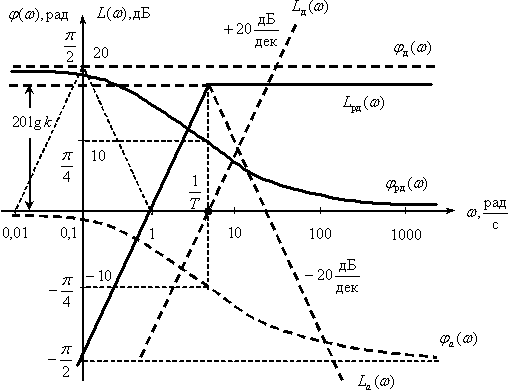
Интегрирующее звено с запаздыванием

Передаточная функция

.

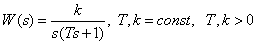Представим звено в следующем виде

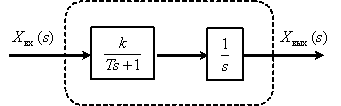
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

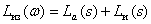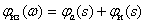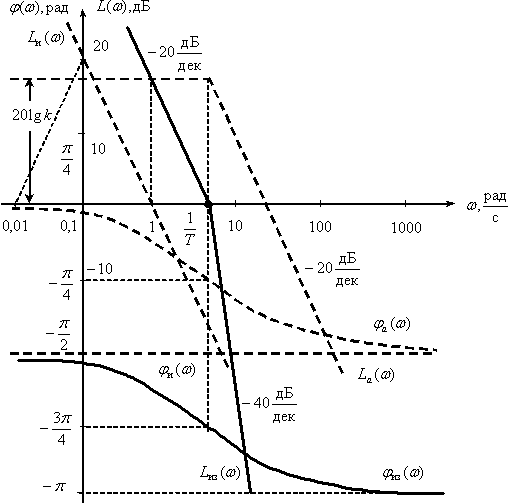
Пропорционально-интегральное звено

Передаточная функция

.

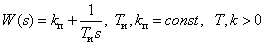Представим звено в следующем виде

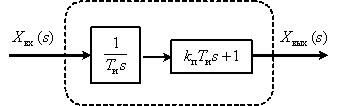
Тогда ЛАЧХ и ЛФЧХ имеют вид –

,

.

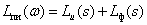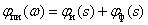Частотные характеристики колебательного звена

Колебательное звено является элементарным динамическим звеном второго порядка, обладает тремя варьируемыми параметрами. Поэтому его характеристикам уделим более пристальное внимание. Тем более, что колебательным звеном описываются достаточно сложные элементы электромеханических систем и электроприводов, на пример, такой распространенный элемент как электродвигатель постоянного тока.

Передаточная функция колебательного звена –

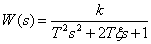(5.9)

где 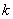– коэффициент усиления, 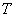– постоянная времени, 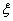– коэффициент затухания.

Отличительной особенностью колебательного звена является то, что оно меняет не только свои свойства, но и название в зависимости от величины коэффициента затухания:

· если 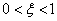– звено называют колебательным, так как его временные характеристики носят колебательный характер;

· если 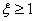– звено называют инерционным (апериодическим) звеном второго порядка, так как его временные характеристики носят монотонный характер, то есть колебания отсутствуют;

· если 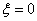– звено называют консервативным, так как его временные характеристики имеют вид незатухающих колебаний, говорят, звено консервирует колебания.

Определим частотную характеристику колебательного звена.

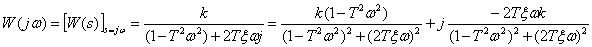(5.10

ВЧХ –

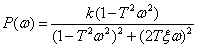(5.11)

МЧХ –

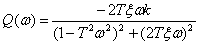(5.12)

АЧХ –

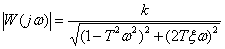(5.13)

ФЧХ –

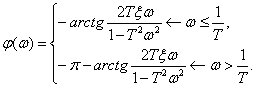(5.14)

Построим ВЧХ и МЧХ на одном графике, примерный вид характеристик показан на рис. 5.5.

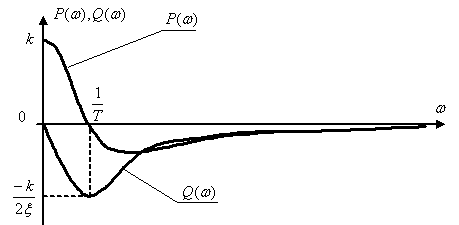
Рис. 5.5

Примерный вид АФЧХ показан на рис. 5.6.

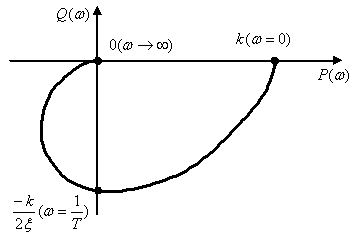
Рис. 5.6

Примерный вид АЧХ и ФЧХ показан на рис. 5.7 и 5.8, функция АЧХ имеет экстремум ( 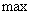) при

.

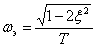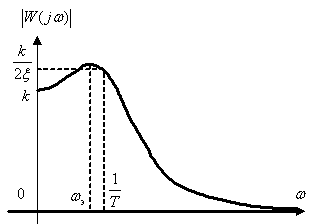
Рис. 5.7

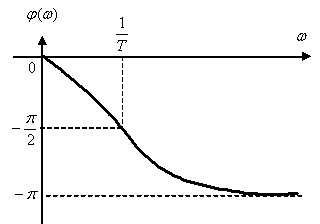
Рис. 5.8

Рассмотрим частотные характеристики консервативного звена ( ).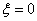

.

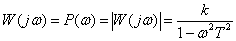При 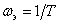характеристики (см. рис. 5.9) имеют разрыв

.

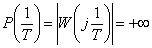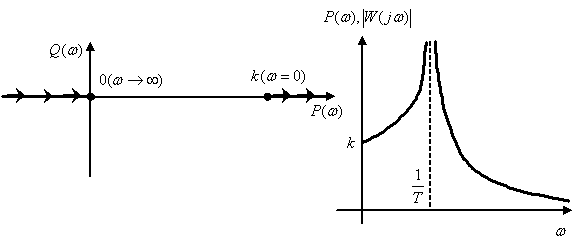
Рис. 5.9

Определим ФЧХ консервативного звена –

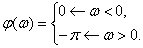
Примерный вид ФЧХ показан на рис. 5.10.

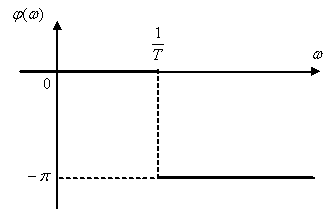
Рис. 5.10

Определим логарифмические характеристики колебательного звена.

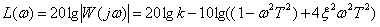(5.15)

Определим асимптотическую ЛАЧХ колебательного звена

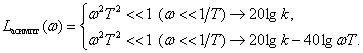
Наклон асимптоты –

.

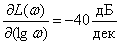Максимальное отклонение асимптотической ЛАЧХ от точной –

.

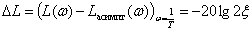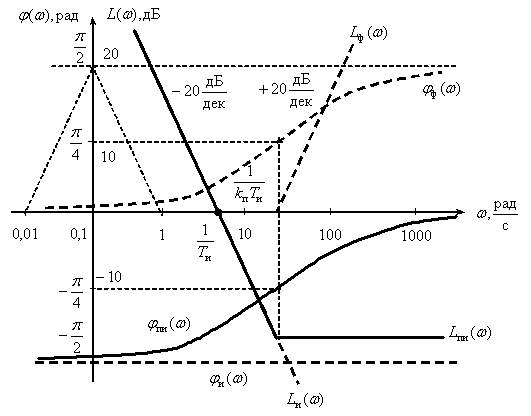
Примерный вид ЛАЧХ и ЛФЧХ показан на рис. 5.11.

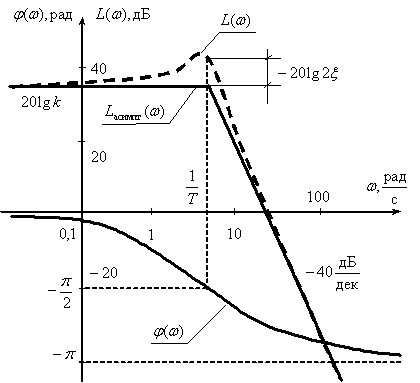
Рис. 5.11

Построение частотных характеристик инерционного звена второго порядка

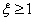( ).Если 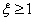, можно преобразовать передаточную функцию звена –

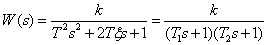(5.16)

где

.

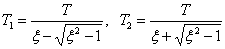Звено с передаточной функцией в виде (5.16), можно представить в идее двух апериодических звеньев, включенных последовательно, как это показано на рис. 5.12.

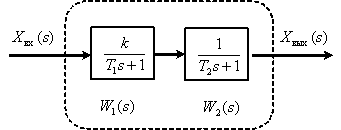
Рис. 5.12

Получим асимптотическую ЛАЧХ для инерционного звена второго порядка, представляя его в виде двух последовательно включенных апериодических звеньев, (см. рис. 5.12).

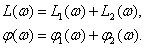
На рис. 5.13 и 5.14показаны ЛАЧХ инерционного звена второго порядка.

Рис. 5.13

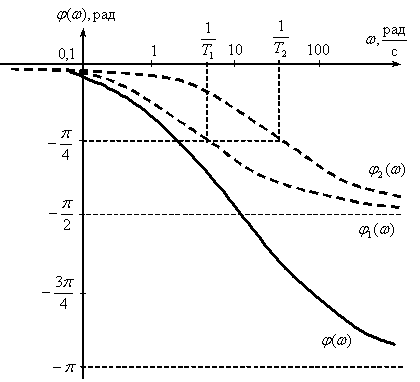
Рис. 5.14

2Построение логарифмических частотных характеристик разомкнутой цепи звеньев

Логарифмические частотные характеристики имеют большое практическое значение. Поэтому рассмотрим их построение. Часто результирующую передаточную функцию смешанного соединения звеньев можно свести к виду

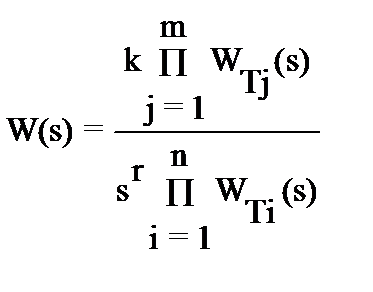, (5.17)

где W_T(s) - передаточная функция типового звена.

В этом случае построение ЛАХ производится по выражению

L(w) = 20lgA(w) = 20lg|W(jw)|=

= 20lgk - r´20lgw + - .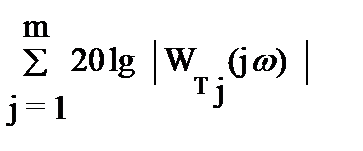

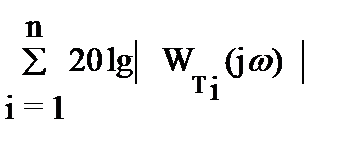Построение ЛФХ производится по выражению

y(w) = argW(jw) = -r´90⁰ + - .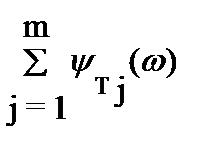

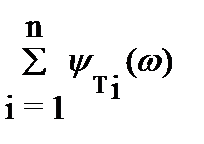Таким образом, результирующаяЛАХ определяется суммированием ЛАХ составляющих типовых звеньев, а результирующая ЛФХ - соответственно суммированием ЛФХ составляющих типовых звеньев. Таблицы характеристик типовых звеньев имеются в литературе.

Асимптотические ЛАХ можно построить непосредственно по виду передаточной функции по следующему правилу, состоящему из четырех пунктов.

1. Частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:

.

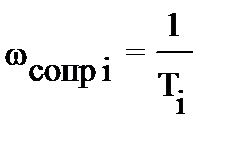Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше.

2. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, имеет наклон -(20´r)дб/дек и проходит через точку с координатами: w=1 с^{-1, L(1)=20lg k дб, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции.}

3. На сопрягающих частотах ЛАХ претерпевает изломы.

3.1. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на -(20´v)дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

3.2. Если сопрягающая частота соответствует постоянной времени Т_i, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20´v) дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Т_i.

4. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.

Рассмотрим более подробно построение ЛАЧХ САР с целью выработки навыков быстрого построения первой асимптоты. Отметим, что при получении ЛАЧХ САР мы будем ориентироваться, как уже говорилось ранее, не на представлении частотной передаточной функции системы в виде отношения полиномов по j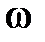

,

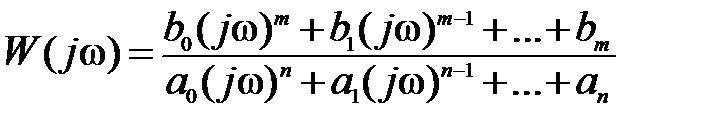а считать и числитель и знаменатель этой функции произведениями комплексных функций вида 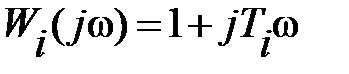любой степени.

Любая частотная передаточная функция 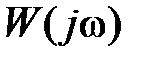может быть отнесена к одному из трех типов. Нужно сказать, что для нахождения типа частотной передаточной функции число скобок вида 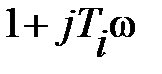в числителе и знаменателе и их степени совсем не критичны. Тип частотной передаточной функции определяется наличием или отсутствием множителя 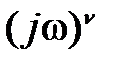( где ν =1,2,3…) в числителе или знаменателе. Если этого множителя нет вообще, то частотная передаточная функция относится к I типу, если он находится в числителе – то ко II–му, а если в знаменателе – то к III типу. Ниже приведены примеры частотных передаточных функций, относящихся к одному из вышеуказанных типов.

I. 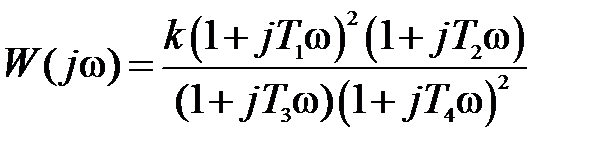. (5.18)

II. 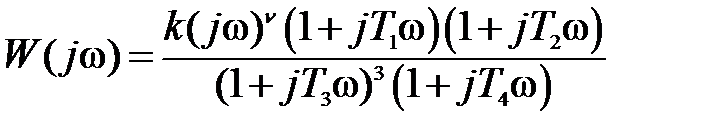. (5.19)

III. 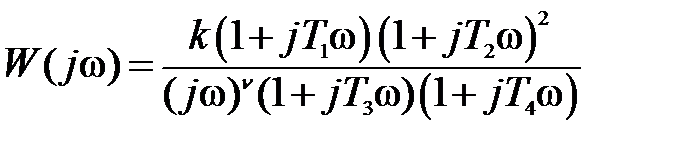. (5.20)

Амплитудная частотная характеристика для каждого из этих примеров различных частотных передаточных функций имеет вид

.

.

.

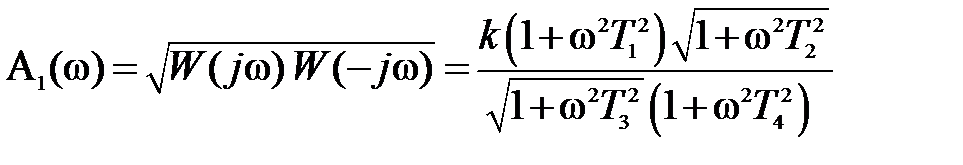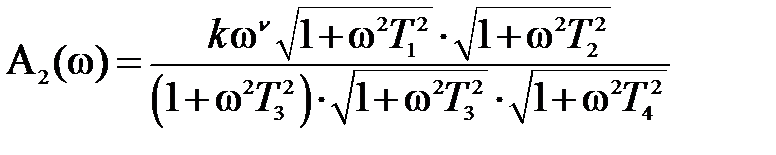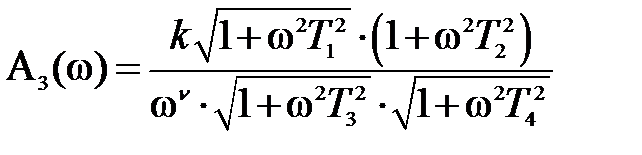Расположим постоянные времени 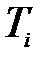в порядке их убывания. Допустим, числовые значения параметров 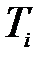таковы, что справедливы соотношения .

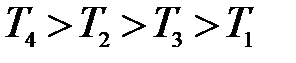Тогда неравенства для сопрягающих частот примут вид

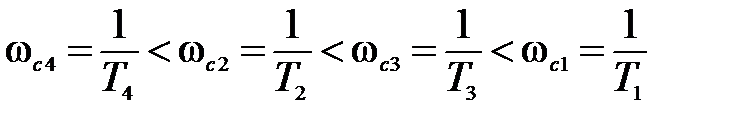. (5.21)

Для I участка частот, когда 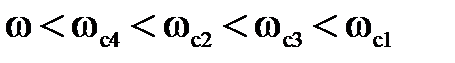, т.е. когда 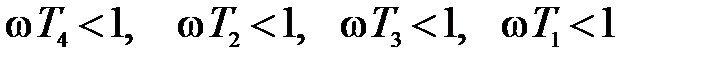в формулах для 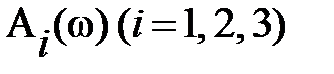в скобках и подкоренных выражениях можно пренебречь вторыми слагаемыми по сравнению с единицей, и тогда для первой асимптоты частотной передаточной функции I, II, III типов, соответственно, получится

,

,

.

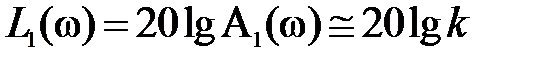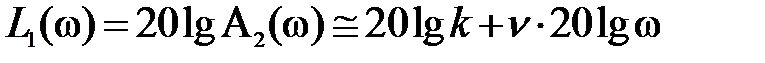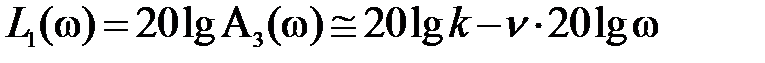Из этих выражений следует, что для частотной передаточной функции I типа первая асимптота есть прямая линия, параллельная оси абсцисс и проходящая от нее на расстоянии 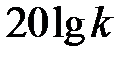; для частотной передаточной функции II типа первая асимптота это прямая линия с наклоном + ν 20 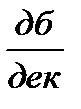, а для частотной передаточной функции III типа – с наклоном - ν 20 .

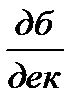Итак, оказывается, найти первую асимптоту САР очень легко. Проведение последующих асимптот – второй, третей и т.д. рассмотрим на примере упругого звена .

Упругое звено описывается дифференциальным уравнением вида

.

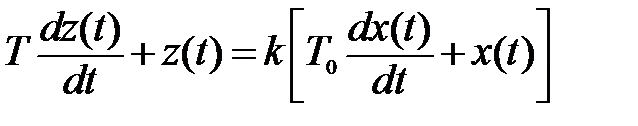Примерами упругого звена (см. рис. 5.15) могут служить пассивные четырехполюсники вида

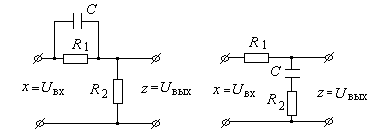
Рис. 5.15. Примеры упругого звена.

Если к вышеприведенному дифференциальному уравнению упругого звена применить преобразование Лапласа, то для нулевых начальных условий получим

,

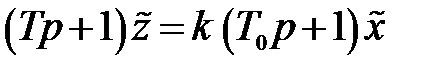и, следовательно, передаточная функция звена будет

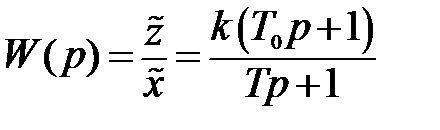. (5.22)

Характеристики упругого звена существенно зависят от параметра 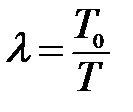. При λ > 1, т.е. при Т₀ > T звено называется упругим дифференцирующим, в противном случае, при λ < 1 – упругим интегрирующим.

Частотная передаточная функция звена, исходя из (5.22), имеет вид

.

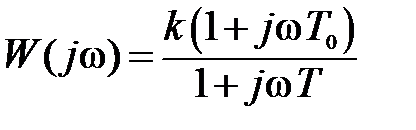Следовательно, амплитудная частотная A( 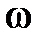) и фазовая частотная φ( 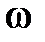) характеристики могут быть представлены следующим образом

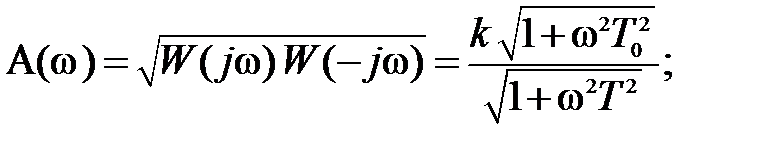
φ 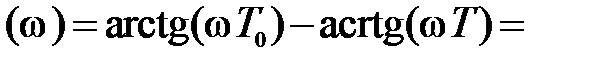φ₁( 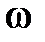) – φ₂( ).

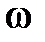Выражение для точной ЛАЧХ определяется следующим образом

.

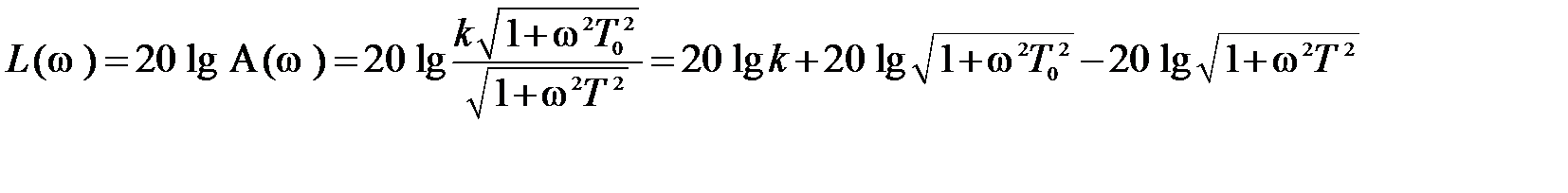Из (5.22) видно, что передаточная функция звена имеет две постоянных времени Т₀ и Т, значит, асимптотическая ЛАЧХ содержит две сопрягающие частоты 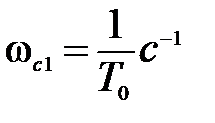и 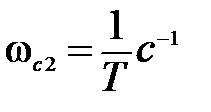, и три частотных участка.

Рассмотрим сначала случай λ >1, т.е. 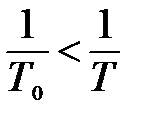(рис. 5.16)

I участок

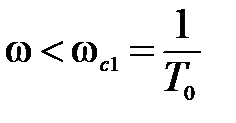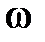, T₀<1.

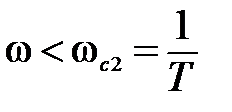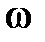, T<1.

Тогда выражение для первой асимптоты с учетом этих неравенств примет вид

.

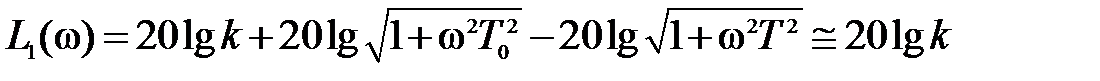Это уравнение прямой, проходящей на I участке параллельно оси абсцисс на расстоянии от нее 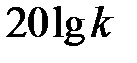(если, допустим, примем, что k = 0.1, то L₁( 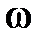) = – 20 дб).

II участок

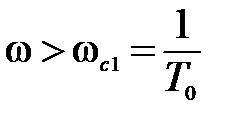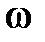, T₀>1.

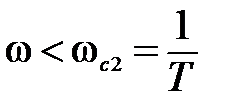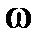, T<1.

С учетом этих неравенств уравнение для второй асимптоты получится из выражения для точной ЛАЧХ в следующем виде

.

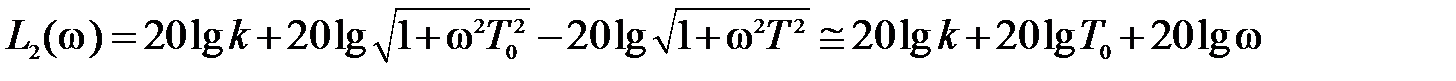Это уравнение прямой, проходящей через конец первой асимптоты с наклоном +20 .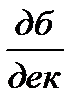

III участок

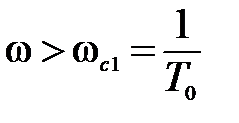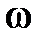, T₀>1.

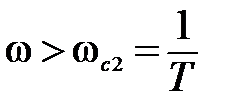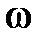, T>1.

Для этого участка уравнение асимптоты примет вид

.

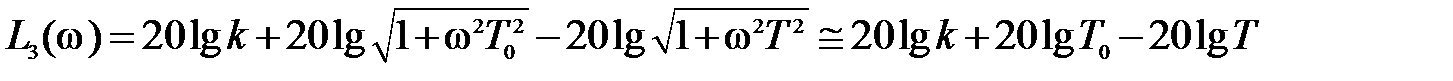Это выражение характеризует горизонтальную прямую, проходящую на расстоянии 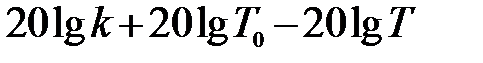от оси абсцисс через конечную точку второй асимптоты.. Вся асимптотическая ЛАЧХ упругого дифференцирующего звена приведена на рис. 5.16.

Построение ЛАЧХ можно сильно упростить, если воспользоваться нижеследующей методикой.

Первая асимптота ЛАЧХ заканчивается на сопрягающей частоте 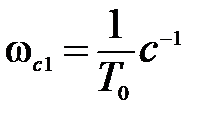, которой соответствует постоянная времени 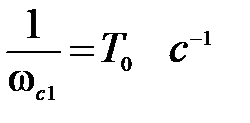. Из выражения для передаточной функции (5.22) видно, что эта постоянная

Рис. III.38. ЛАЧХ упругого

дифференцирующего звена (λ >1).

времени расположена в скобке 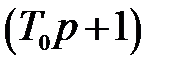, находящейся в числителе. Известно мнемоническое правило, что если скобка 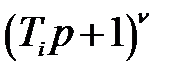находится в числителе, то ЛАЧХ на частоте 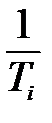претерпевает излом на + 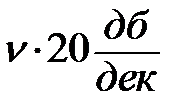, а если в знаменателе, то .

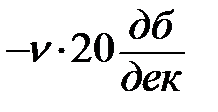В нашем случае 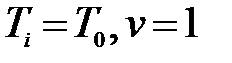, и, следовательно, ЛАЧХ “ломается” на +20 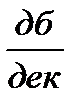. Поэтому, раз наклон первой асимптоты был ноль, а на частоте 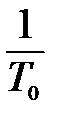ЛАЧХ изменила его на +20 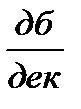, то наклон ЛАЧХ на II участке будет 0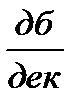+20 = 20 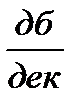. Сопрягающей частоте 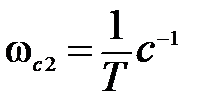соответствует постоянная времени Т с, которая, как видно из (5.22) расположена в скобке, находящейся в знаменателе. Значит, на частоте 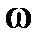_c2 ЛАЧХ претерпевает излом на -20 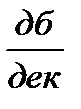и наклон ЛАЧХ на III участке будет

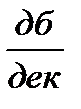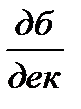+20 -20 = 0.

Рассмотрим теперь случай λ <1, т.е 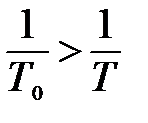(рис. 5.17).

I участок.

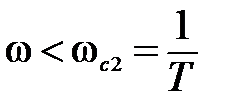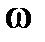, T<1.

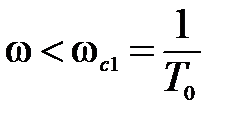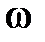, T₀ <1.

Выражение для первой асимптоты выглядит следующим образом.

.

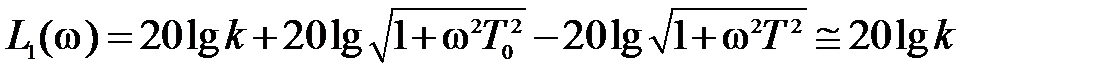Итак, первая асимптота – прямая линия, параллельная оси частот и отстоящая от нее на расстоянии 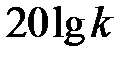( например, при k = 1000 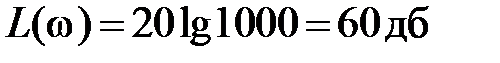). Первая асимптота заканчивается частотой 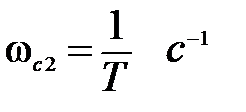, которой соответствует постоянная времени Т, расположенная в скобке, находящейся в знаменателе передаточной функции звена. Значит, ЛАЧХ на частоте 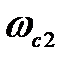претерпевает излом на -20 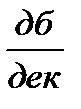, а вторая асимптота будет проходить с наклоном 0 –20 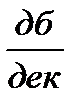= – 20 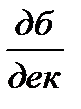до сопрягающей частоты 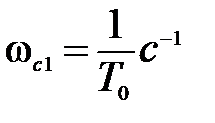. Этой частоте соответствует постоянная времени Т₀, расположенная в скобке числителя (5.22). 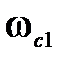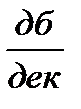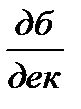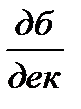Следовательно, ЛАЧХ на частоте “изломается” на +20 и суммарный наклон ЛАЧХ на III участке будет -20 + 20 = 0.

Рис. 5.17. ЛАЧХ упругого интегрирующего звена (λ < 1).

Из сказанного понятно, что на всех участках, кроме первого, определить наклон асимптот ЛАЧХ указанным способом не представляет сложности. Ниже будет показано, как также просто построить и первую асимптоту.

Построим ЛАЧХ для частотных передаточных функций всех трех типов.

Для ЛАЧХ I типа (рис. 5.18) при, например, k = 100 первая асимптота L₁( ) проходит на расстоянии 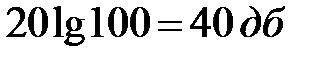параллельно оси абсцисс. Если сопрягающие частоты подчиняются неравенствам (5.21), то при частоте 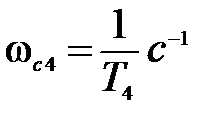, соответствующей постоянной времени Т₄, находящейся в знаменателе (5.18) в скобке со степенью ν = 2, асимптота претерпевает излом 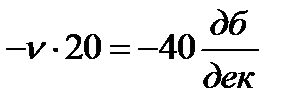, так что наклон второй асимптоты будет 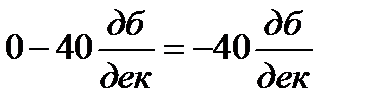. При частоте 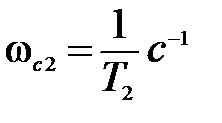, соответствующей постоянной времени Т₂, находящейся в числителе (5.18), происходит излом асимптоты на 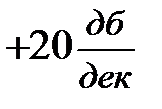и суммарный наклон асимптоты на III участке будет 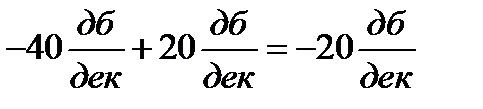. Рассуждая аналогично предыдущему, найдем, что при частоте 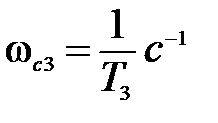происходит дополнительный излом асимптоты на 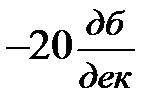, а при частоте 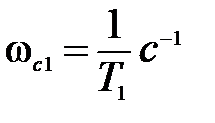– на .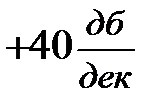

Рис. 5.18. ЛАЧХ для частотной передаточной

функции САР I типа.

Для ЛАЧХ II типа при k = 0.1 и ν = 2 первая асимптота, как уже говорилось, может быть представлена в виде

.

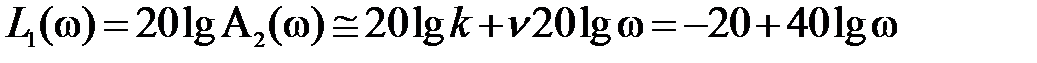Это прямая линия с наклоном 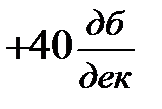; проходящая для любой конкретной частоты 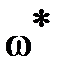через точку, значение ординаты которой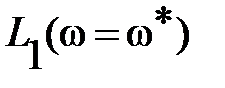 . Рекомендуется для простоты расчетов брать 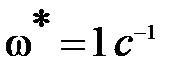, независимо от того, принадлежит ли частота 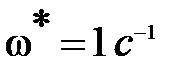I участку или нет. Для нашего случая (рис. 5.19)

.

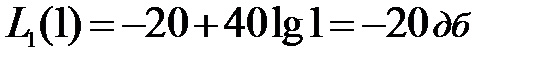Асимптота I участка с наклоном 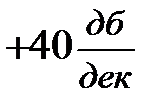проходит через точку 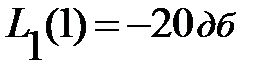, расположенную на II участке. До сопрягающей частоты 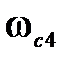асимптота изображена сплошной линией, а после нее до точки 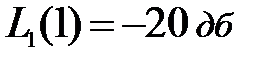- пунктиром. На сопрягающей частоте 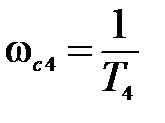ЛАЧХ претерпевает излом на 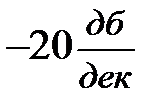(5.19) и суммарный наклон второй асимптоты будет 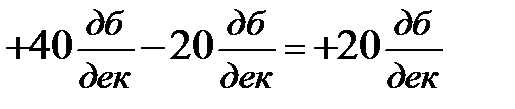. Построение дальнейших асимптот аналогично вышерассмотренному и приведено на рис. 5.19.

Рис. 5.19. ЛАЧХ для частотной

передаточной функции САР II типа.

И, наконец, в случае частотной передаточной функции III типа при

k = 1.0 и ν = 1 первая асимптота ЛАЧХ будет иметь вид

.

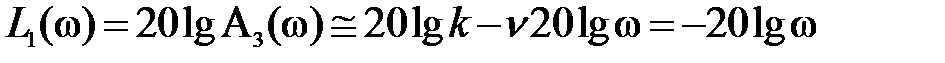Итак, первая асимптота здесь – прямая линия с наклоном 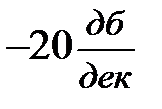, проходящая через точку 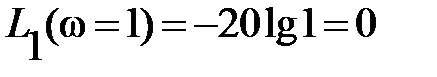(рис. 5.20). Далее на сопрягающей частоте 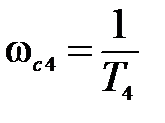(5.20) ЛАЧХ ломается на 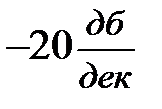, так что наклон второй асимптоты будет 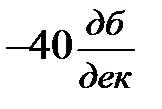. Построение дальнейших асимптот легко уяснить из рис. III. 42 и (5.20).