Типовые практические задания. Формы контроля:тестирование, письменное решение задач, устный опрос
Семестр 3
Формы контроля:тестирование, письменное решение задач, устный опрос
Последовательность и условия выполнения задания:
1. 1. Компьютерное тестирование.
2. Решение задач из экзаменационного билета.
3. Устный ответ на теоретический вопрос билета.
4. Устный опрос на знание основных формул и определений.
Вы можете воспользоваться: -
Максимальное время выполнения задания – 20 минут тестирование и 20 минут решение задач билета.
Теоретические вопросы
1. Определения высказывания. Определение таблицы истинности высказывания. Конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция, инверсия (отрицание) высказываний, их определение, обозначение и таблицы истинности.
2. Тождественно-истинные и тождественно-ложные формулы; равносильные формулы.
3. Законы алгебры логики (с доказательством).
4. Понятие булевой функции. Булевы функции одной переменной. Булевы функции двух переменных. Количество булевых функций n переменных.
5. Стрелка Пирса, определение, таблица истинности, свойства.
6. Штрих Шеффера, определение, таблица истинности, свойства.
7. Совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ). Методика представления булевой функции в виде совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).
8. Минимизация СДНФ и СКНФ с помощью карт Карно (алгоритм). Правила объединения 1 (0) в контур.
9. Предикаты и кванторы. Способы получения высказываний из предикатов. Кванторные операции над предикатами.
10. Понятие множества, пустого множества, универсума.
11. Графическое изображение множеств (диаграммы Эйлера-Венна).
12. Способы задания множеств.
13. Операции над множествами (объединение, пересечение, дополнение, разность, симметрическая разность) и их связь с логическими операциями.
14. Мощность множества. Принцип включения и исключения.
15. Декартовое (прямое произведение множеств). Степень множества.
16. Подмножество множества. Отношения на множествах. Изображение отношения графом. Матрица отношения.
17. Свойства отношений на множестве (рефлексивное, симметричное, транзитивное, полное).
18. Матрицы. Действия над матрицами (сложение и вычитание матриц, умножение матрицы на число, транспонирование матрицы, умножение матриц). Свойства действий над матрицами.
19. Виды матриц. Алгоритм составления обратной матрицы.
20. Определитель матрицы. Правило треугольников. Теорема о разложении определителя по элементам строки или столбца.
21. Свойства определителя.
22. Системы линейных уравнений. Метод обратной матрицы.
23. Системы линейных уравнений. Метод Крамера.
24. Системы линейных уравнений. Метод Гаусса.
25. Вектор. Виды векторов.
26. Действия над векторами (сумма и разность векторов, произведение вектора на число, скалярное, векторное и смешанное произведения векторов). Свойства действий над векторами.
27. Определение координат вектора в пространстве.
28. Действия над векторами в координатах (сложение, вычитание, скалярное произведение, векторное произведение, смешанное произведение векторов, умножение вектора на число).
29. Простейшие задачи в координатах: длина вектора, угол между векторами, координаты середины отрезка, расстояние между двумя точками.
30. Критерий коллинеарности векторов. Критерий перпендикулярности векторов. Критерий компланарности векторов.
31. Уравнение прямой с нормальным вектором.
32. Уравнение прямой с направляющим вектором.
33. Уравнение прямой проходящей через две точки. Уравнение прямой с угловым коэффициентом.
34. Общее уравнение прямой, его частные случаи.
35. Критерий параллельности прямых.
36. Окружность, её каноническое уравнение (с выводом уравнения).
37. Эллипс, его элементы, каноническое уравнение, эксцентриситет. Оптическое свойство эллипса.
38. Гипербола, её элементы, каноническое уравнение, эксцентриситет, уравнения асимптот. Оптическое свойство гиперболы.
39. Парабола, её каноническое уравнение, уравнение директрисы. Оптическое свойство параболы.
Типовые практические задания
1. Выберите высказывания, которые является истинными, если высказывание P-истинно, а высказывание Q -ложно?
PÙQ, PÚQ, P®Q, P«Q, P 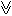 Q.
Q.
2. Выберите высказывания, которые является истинными, если высказывания P и Q ложны?
P∼Q, PÚQ, Q®P, P 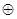 Q.
Q.
3. Составить таблицу истинности для функции, найти ее СДНФ и СКНФ, минимизировать полученные СДНФ и СКНФ с помощью карт Карно:
a) 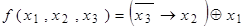
b) 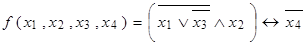
4. Для функции найти СДНФ и СКНФ, минимизировать СДНФ и СКНФ с помощью карт Карно:
a) 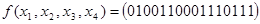
b) 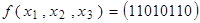
5. Формализуйте высказывание «Если мало спать и пить много кофе, то наутро будет болеть голова», найдите СДНФ и СКНФ, минимизировать полученные СДНФ и СКНФ с помощью карт Карно.
6. Запишите с помощью формулы логики высказывание «Импликация высказываний А и В примет значение «ложь», тогда и только тогда, когда высказывание А примет значение «истина» и высказывание В примет значение «ложь», найдите СДНФ и СКНФ, МДНФ и МКНФ.
7. Пусть Р(х) — предикат: «х — делится на два ». Выразите словами высказывания $х Р(х);
"х Р(х).
8. P(x): x – отрицательное число, Q(x,y): x > y, R(x,y) : студент x изучает дисциплину y. Определить, истинными или ложными являются высказывания, построенные из предикатов:
a. 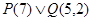 ,
,
b. 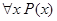 ,
,
c. 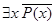 ,
,
d. 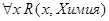 ,
,
e. 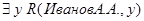 ,
,
9. Q(x,y): студент x учится в колледже y. Запишите на естественном языке высказывания и определите их истинность:
a) 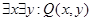 ,
,
b) 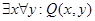 ,
,
c) 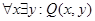 ,
,
d) 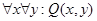 ,
,
e) 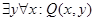 ,
,
f) 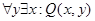 .
.
10. По каналу связи передаются 3 сообщения, каждое из которых может быть правильно принято, независимо от других. Запишите с помощью формул алгебры логики высказывания, если 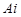 -« сообщение i принято правильно», i=1..3;:
-« сообщение i принято правильно», i=1..3;:
a) В-«все сообщения будут искажены»;
b) С-«будет искажено только первое сообщение»;
c) D-«одно сообщение будет искажено»;
d) E-«хотя бы одно сообщение будет искажено».
11. Определите значение истинности выражения:
a) (NOT (Истина ANDЛожь)OR (NOT Истина ) )ХOR Истина
b) NOT ( (ИстинаХOR Ложь)AND(ИстинаOR Истина) )
12. Определите значение истинности выражения ((x ≠ 3)OR(x > 6))AND (NOT (x ≤ 4))) при заданных значениях переменной:
a) при x = 5
b) при x = 4
c) при x = 2
13. Составьте предикат (логическое выражение), которое примет значение true, если будет выполнено условие:
a) Среди чисел а, b, с есть хотя бы одна пара взаимно противоположных.
b) Данные числа х, у являются координатами точки, лежащей в первой координатной четверти.
c) Шахматный конь за один ход может переместиться с одного заданного поля на другое (каждое поле задано двумя координатами — целыми числами от 1 до 8).
d) Число d является корнем только одного из уравнений 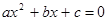 и
и 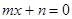 .
.
e) число, введенное с клавиатуры, больше 100 и делится нацело на 3;
f) хотя бы одно из трех чисел a, b, c введенных с клавиатуры больше 100.
14. Упростить 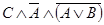 с помощью законов логики. Сделать проверку с помощью таблиц истинности.
с помощью законов логики. Сделать проверку с помощью таблиц истинности.
15. Упростить 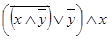 с помощью законов логики. Сделать проверку с помощью таблиц истинности.
с помощью законов логики. Сделать проверку с помощью таблиц истинности.
16. Упростить 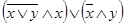 с помощью законов логики. Сделать проверку с помощью таблиц истинности.
с помощью законов логики. Сделать проверку с помощью таблиц истинности.
17. Даны два множества A = {§, ©, ª}, B = {©, ¨, ·}. Что представляет собой множества А\В, А È В, АÇВ, В\А, ВΔА?
18. Найдите (BÈ А)\C, AÇ (B\C), (CÇ А)È B, (CΔ А) Ç B,если 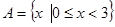 ,
, 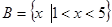 ,
, 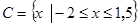 .
.
19. Три множества A, В и С изображены кругами Эйлера. Запишите множество, которое соответствует закрашенной области:
a) 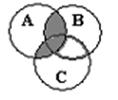 b)
b) 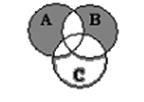
20. Изобразите множества кругами Эйлера:
a) 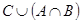 , если
, если 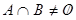 ,
, 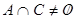 ,
, 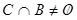 ;
;
b) 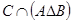 , если
, если 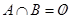 ,
, 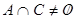 ,
, 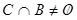 ;
;
c) 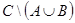 , если
, если 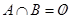 ,
, 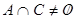 ,
, 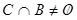 ;
;
d) 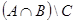 , если
, если 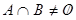 ,
, 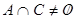 ,
, 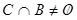 .
.
21. Определите мощность множества:
a) 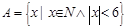 .
.
b) 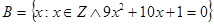 .
.
22. Из 105 опрошенных человек 38 любят смотреть по телевизору фильмы ужасов, 29 − мелодрамы, 65 − комедии, смотрят фильмы ужасов или мелодрамы − 56, смотрят комедии или мелодрамы − 81, смотрят фильмы ужасов или комедии − 91, не смотрят телевизор вообще 4 человека. Сколько человек смотрят только комедии?
23. На экзамене по дискретной математике из 45 человек группы первое задание выполнили 17 человек, второе – 20, третье – 20, первое и второе – 5, второе и третье – 7, первое и третье – 6, все три – 4. Сколько студентов не выполнили ни одного задания?
24. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» используется символ «&». Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
фрегат & эсминец 1000
фрегат 2000
эсминец 2500
Сколько страниц будет найдено по запросу
фрегат | эсминец
25. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» используется символ «&». Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
васильки & ландыши 650
ландыши & лютики 230
ландыши & (васильки | лютики) 740
Сколько страниц будет найдено по запросу
ландыши & васильки & лютики
26. Вычислить определитель 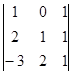 . Найти миноры М12 , М22 , алгебраическое дополнения А12 , А22.
. Найти миноры М12 , М22 , алгебраическое дополнения А12 , А22.
27. Вычислить определитель по теореме о разложении по элементам строки или столбца 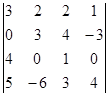 .
.
28. Найти матрицу, обратную матрице 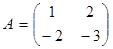 . Сделать проверку.
. Сделать проверку.
29. Найти матрицу, обратную матрице 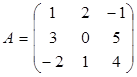 . Сделать проверку.
. Сделать проверку.
30. Вычислить 2B∙АТ, если, 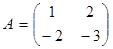 ,
, 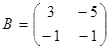 .
.
31. Вычислить B-1-2CТ, если, 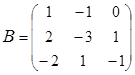 ,
, 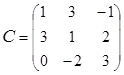 .
.
32. Найдите определитель матрицы 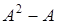 , если
, если 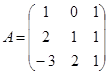 .
.
33. Решить систему методом Крамера 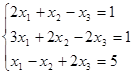 .
.
34. Решить систему методом обратной матрицы 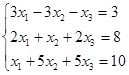 .
.
35. Решить систему уравнений методом Гаусса:
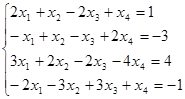 ,
, 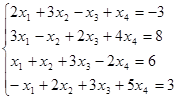 .
.
36. ABCDA1B1C1D1-куб c ребром 1, E – середина СС1. Найдите:
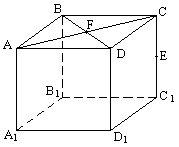
а) 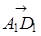
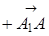 ;
;
б) 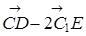 ;
;
в) 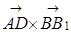 ;
;
г) 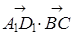 ;
;
д) 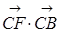 ;
;
e) 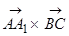 ;
;
ж) 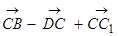 .
.
37. Для векторов 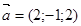 и
и 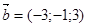 найдите: 1)
найдите: 1) 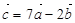 ;
;
2) 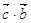 ; 3)
; 3) 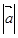 ; 4)
; 4) 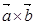 5)
5) 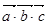 . Будут ли вектора
. Будут ли вектора 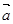 и
и 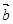 коллинеарными?
коллинеарными?
38. Определить коллинеарные вектора среди заданных: 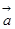 =(1;-4;0),
=(1;-4;0), 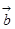 =(5;20;0),
=(5;20;0),
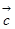 =(-2; 8;0),
=(-2; 8;0), 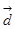 =(4;1;5).
=(4;1;5).
39. Определить перпендикулярные и коллинеарные векторы среди заданных:
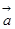 =(1;-4;0),
=(1;-4;0), 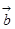 =(5;20;0),
=(5;20;0), 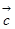 =(-2; 8;0),
=(-2; 8;0), 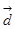 =(4;1;5).
=(4;1;5).
40. Найдите угол В и координаты векторов 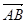 ,
, 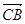 треугольника АBC, если А(-1;2;4), B(2;5;7), С(5;8;4).
треугольника АBC, если А(-1;2;4), B(2;5;7), С(5;8;4).
41. Найти объем пирамиды MNKL и площади ее граней, если M(0;0;1),
N(1;1;2), K(-1;1;3), L(0;2;0).
42. Какие линии на плоскости задаются уравненениями:
a. 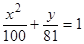
b. 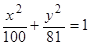
c. 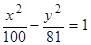
d. 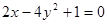
e. 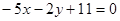
f. 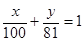
43. Найдите пары параллельных прямых из следующих:
a. 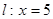 и
и 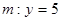
b. 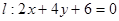 и
и 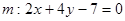
c. 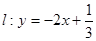 и
и 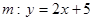
d. 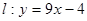 и
и 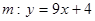
44. Найти уравнения сторон треугольника ABC, если A(-1;3), B(;2;-2), C(0;1).
45. Найти уравнения высот треугольника ABC, если A(1;8), B(0;-2), C(4;1).
46. Написать уравнение гиперболы, эксцентриситет которой равен 4, а мнимая ось
равна 8. Сделать чертеж.
47. Составить уравнение гиперболы, если действительная полуось равна 6, а эксцентриситет равен 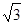 . Сделать чертеж.
. Сделать чертеж.
48. Составить уравнение эллипса, если большая ось равна 6 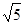 , а эксцентриситет равен 2
, а эксцентриситет равен 2 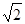 /3. Сделать чертеж.
/3. Сделать чертеж.
49. Cоставить уравнение эллипса, если фокусами его являются точки (±7,0) и эксцентриситет равен 1/ 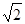 . Сделать чертеж.
. Сделать чертеж.
50. Найти уравнение параболы с фокусом в точке 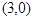 и директрисой х= -1. Сделать чертеж.
и директрисой х= -1. Сделать чертеж.
51. Найти уравнение окружности с центром в точке 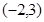 и проходящей через точку
и проходящей через точку 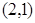 . Сделать чертеж.
. Сделать чертеж.
52. Составьте логическое выражение, которое примет значение true, если точка с координатами (x,y) попадет в закрашенную область, значение false, если не попадет:
а) 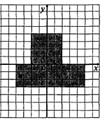 б)
б)  в)
в) 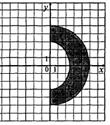 г)
г) 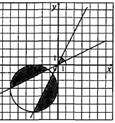 д)
д) 
