Теоретические основы работы

ВВЕДЕНИЕ

Расчетно-графические работы по курсу «Теория колебаний» являются частью учебной программы по этой дисциплине и направлены на закрепление навыков в области расчетов механических колебаний элементов горных и буровых машин, мачт и вышек, канатов, бурильных труб и породоразрушающих инструментов.

Цель выполнения указанных расчетно-графических работ (РГР) состоит в том, чтобы научить будущих горных инженеров (механиков и буровиков) определять законы и параметры колебаний изучаемых механических систем и на этой основе оценивать уровни их динамической нагруженности, что необходимо для дальнейших прочностных расчетов.

Задачей РГР является развитие навыков самостоятельного построения студентами расчетных схем для изучения колебательных систем, анализа их динамического состояния для последующей выработки рекомендаций по повышению эффективности и надежности горно-буровых установок, элементов их конструкций, а также вспомогательного оборудования.

Теоретической основой для выполнения расчетно-графических работ являются прослушанные студентами дисциплины: «Теоретическая механика», «Основы теории механических колебаний», а также курс «Математика».

Собственные колебания консервативной системы с одной степенью свободы вблизи положения устойчивого равновесия

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Работа состоит из двух частей: свободные колебания и затухающие колебания при общей схеме колебательного механизма и общих начальных условиях.

Свободные колебания. Колебательная система считается консервативной, если полная энергия в ней не убывает и в нее не поступает энергия из внешнего источника, т.е. справедливо условие:

,

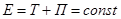где Е – полная энергия; Т, П – соответственно кинетическая и потенциальная энергии, которые могут изменяться, но сумма их сохраняется постоянной (отсюда название системы).

Для тела, совершающего возвратно-поступательное движение, кинетическая энергия равна:

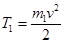, (1.1)

где m₁ – масса движущего тела, кг; v - его линейная скорость, м/с.

При вращении тела вокруг неподвижной оси

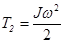, (1.2)

где J – момент инерции тела относительно оси вращения, кг×м²; 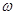- угловая скорость, рад/с.

При совершении телом плоского (плоскопараллельного) движения

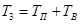, (1.3)

где 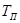- кинетическая энергия поступательного движения, см. формулу (1.1); 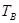- то же для вращательного движения, см. формулу (1.2).

В общем случае кинетическая энергия системы есть сумма кинетических энергий отдельных ее элементов:

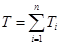, (1.4)

где n – число элементов; T_i – кинетическая энергия какого-либо отдельного элемента.

Потенциальная энергия определяется изменением координаты тела:

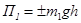, (1.5)

где 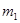- масса тела, кг; 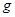- ускорение силы тяжести, 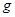=9,81 м/с²; 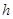- изменение координаты, м.

При этом потенциальная энергия возрастает, если координата увеличивается (знак + в формуле 1.5) и уменьшается в случае уменьшения координаты (знак - в формуле 1.5).

Для пружины потенциальная энергия равна

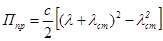, (1.6)

где с – линейная жесткость пружины, Н/м; 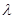- динамическая деформация, м; 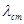- статическая деформация пружины, м.

Потенциальная энергия отдельных элементов суммируется:

,

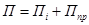где i = 1, 2, 3,….

Полученные общие выражения для полной кинетической и полной потенциальной энергий системы подставляются в уравнение Лагранжа второго рода:

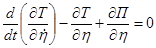, (1.7)

где t – время; 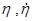- соответственно обобщенные координата и скорость.

После процедур взятия производных для уравнения Лагранжа получаем дифференциальное уравнение вида:

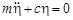, (1.8)

где 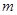- обобщенная масса системы (см. пример решения задачи), кг; 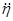- деформация подвески груза при его колебаниях, м.

Для решения уравнения (1.8) должны быть заданы начальные условия:

1) при 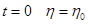- начальная координата;

2) при 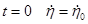- начальная скорость.

Характеристическое уравнение для решения дифференциального уравнения (1.8) имеет вид:

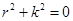, (1.9)

где r – корни характеристического уравнения; 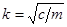- круговая частота колебаний, рад/с.

Корни уравнения (1.9) являются мнимыми и сопряженными, и тогда решением уравнения (1.8) будет:

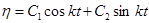, (1.10)

где С₁, С₂ – постоянные интегрирования, определяемые из начальных условий: 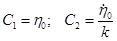. Для использования второго начального условия определена производная от 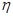по времени:

.

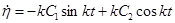С учетом значений С₁, С₂ решение (1.10) примет вид:

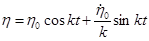. (1.11)

Решение (1.11) может быть представлено в другом виде, удобном для построения графика колебаний:

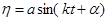(1.12)

при 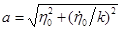и ,

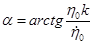где 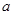- амплитуда колебаний, м; 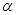- начальная фаза колебаний.

При построении графика следует учесть, что период колебаний равен 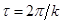. Построение графика показано в примере решения задач.

Затухающие колебания. Данные колебания имеют место, если в колебательную систему ввести некоторую силу сопротивления:

,

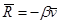где 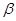- коэффициент демпфирования; 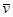- скорость перемещения колеблющегося элемента, м/с.

Сила 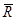пропорциональна скорости в первой степени и носит название вязкого сопротивления.

Дифференциальное уравнение затухающих колебаний:

,

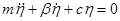которое может быть приведено к следующему виду:

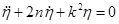, (1.13)

пр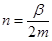и и ,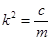

где 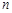- удельный коэффициент демпфирования, рад/с.

Решение уравнения (1.13) может иметь периодический характер при 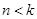(этот случай и будет рассмотрен в настоящей работе):

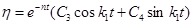, (1.14)

где 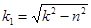- круговая частота затухающих колебаний, рад/с; 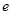- основание натурального логарифма; С₃, С₄ – постоянные интегрирования, определяемые из начальных условий, аналогичных для условий (1.8).

Для использования второго начального условия, по аналогии со свободными колебаниями, возьмем производную от уравнения (1.13) по времени:

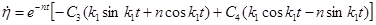. (1.15)

Подстановка начальных условий в уравнения (1.14) и (1.15) дает возможность определения С₃, С₄:

.

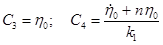С учетом значений С₃ и С₄ решение (1.14) может быть представлено в двух формах:

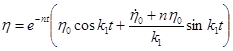; (1.16)

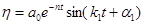, (1.17)

где 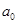- начальная амплитуда затухающих колебаний; 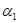- начальная фаза этих колебаний:

;

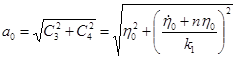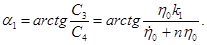
Для построения графика затухающих колебаний целесообразно использовать решение в форме (1.17). Решение (1.16) можно оставить, если не требуется строить график.

С целью проверки решений для свободных и затухающих колебаний можно использовать следующие неравенства: 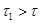; ; 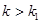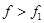, где 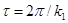- период затухающих колебаний, с; 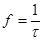- абсолютная частота свободных колебаний, Гц; 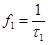- то же для затухающих колебаний, Гц; .

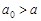Для характеристики затухающих колебаний следует определить декременты затухания колебаний:

- обыкновенный: 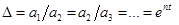, где 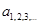- соседние амплитуды по одну сторону оси абсцисс (оси t);

- логарифмический: 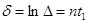.