Определение ускорений точек и звеньев механизма
CИЛОВОЙ РАСЧЕТ МЕХАНИЗМА ДВИГАТЕЛЯ
Определение ускорений точек и звеньев механизма
Последовательность построение плана ускорений (как и плана скоростей) определяется формулой строения механизма: сначала строим для кривошипа АОС, затем для структурных групп 2-3 и 4-5.
Кривошип 1 не движется равномерно: в каких-то моментах он будет двигаться или ускоренно или замедленно,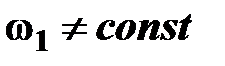 
, 
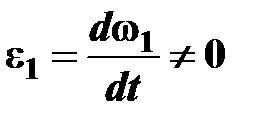, поэтому ускорение точки А представляет собой векторную сумму ускорений
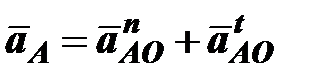м/с2,
где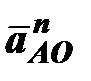 
– нормальное ускорение точки А вокруг точки О;
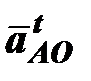– тангенциальное ускорение точки А вокруг точки О.
Нормальное ускорение определяется по формуле
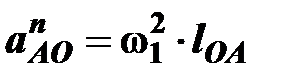м/с2,
где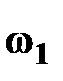 
– угловая скорость кривошипа в рассматриваемом положении, с-1, табл. 5.11;
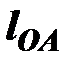– длина кривошипа, м.
Ускорение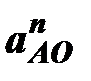 
направлено вдоль звена ОА к центру вращения точке, т.е. от точки А к точке О (рис. 6.1).
Касательное ускорение вычисляется по уравнению
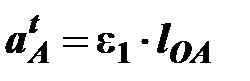м/с2,
где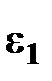 
– угловое ускорение кривошипа в рассматриваемом положении, с-2 .
Угловое ускорение 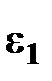определяется по уравнению движения машинного агрегата в дифференциальной форме
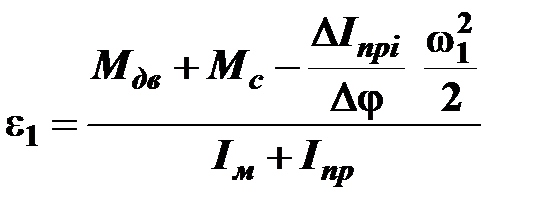с-2, (6.1)
где Mдв, Mс – моменты движущих сил (табл.5.7) и сил сопротивления (табл.5.8), Н×м;
DIпр – приращение приведенного момента инерции, кг,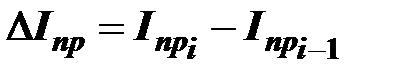 
;
, 
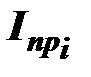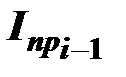– приведенные моменты инерции в текущем и предыдущем положении кривошипа, кг×м2;
Dj – приращение угла поворота кривошипа,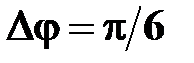 
, рад;
w1 – угловая скорость кривошипа в данном положении табл. 5.11, с-1;
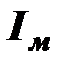– момент инерции маховика.
Масштабный коэффициент плана ускорений рассчитывается по формуле
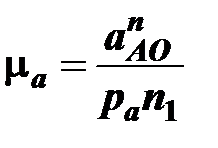м/с2/(мм),
где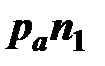 
– длина отрезка, изображающего на плане ускорений нормальное ускорение точки 
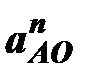, pan1=70…80 мм.
Отрезок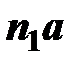 
, который изображает на плане ускорений, ускорение 
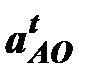рассчитывается по формуле
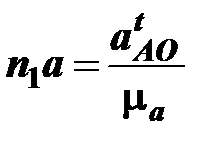мм.
Для определения ускорения точки В воспользуемся уравнением Эйлера
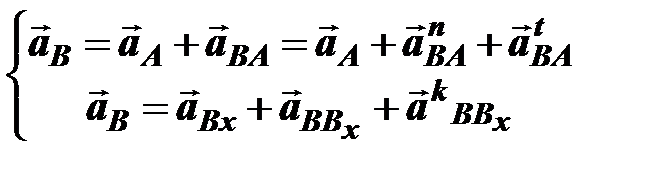(6.2)
где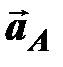 
– переносное ускорение точки А;
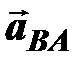– относительное ускорение точки В вокруг А, это ускорение раскладывается на две составляющие – 
,
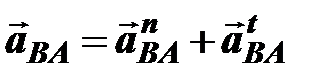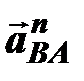– относительное нормальное ускорение точки В вокруг точки А, оно известно по абсолютной величине и по направлению: направлено параллельно звену AB, от точки В к точке А (т.В ®т.А) (рис.6.1), численное значение этого ускорения вычисляется по равенству
,
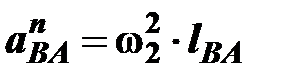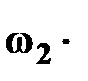– угловая скорость звена 2,указана в табл. 4.1.
На плане ускорений ускорение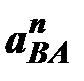 
отображается в виде отрезка 
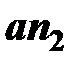, величина которого равна
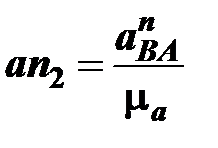мм;
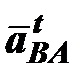– относительное тангенциальное ускорение точки В вокруг точки А, оно неизвестно по абсолютной величине и известно по направлению: направлено перпендикулярно звену AB;
аВх – ускорение точки в переносном вращательном движении с направляющей х-х, аВх=0;
аВBх – ускорение точки В в поступательном движении относительно точки Вх, оно направлено параллельно оси х-х;
акВВх – относительное кориолисово ускорение, акВВх=0.
Построение плана ускорений структурной группы 2-3 производится в такой последовательности (рис. 6.1): из произвольно выбранной точки pa – полюса плана скоростей, проводим отрезок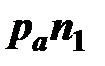 
(изображает ускорение 
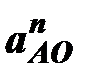) параллельно звену ОА от точки А к точке О. Из точки 
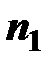строится отрезок 
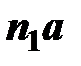(изображает ускорение 
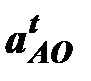), его направление определяется направлением углового ускорения 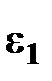. Далее строится вектор полного ускорения 
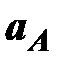– отрезок 
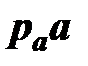. После этого согласно первому уравнению системы (1) из точки а откладываем вектор 
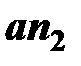(изображает ускорение 
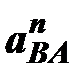), затем из полученной точки 
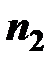проводим прямую перпендикулярную звену АВ, которая является линией действия неизвестного по величине тангенциального ускорения 
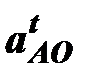. Все слагаемые из первого уравнения системы (6.2) использованы, поэтому переходим ко второму уравнению. В этом уравнении осталось неравным нулю только относительное ускорение аВBх, о котором на данном этапе известно только его направление. В связи с этим из полюса pa проводим прямую параллельную оси цилиндра х-х. Данная и проведенная раннее прямые пересеклись, тем самым определили решение уравнений – точку b. На основании построенного плана получили значения ускорений
,
,
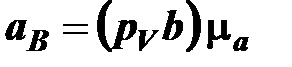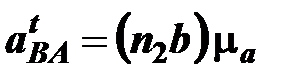и углового ускорения звена 2
.
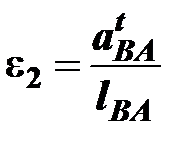Чтобы определить направление углового ускорения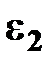 
, следует мысленно разметить вектор 
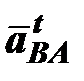в точку В. Направление вращения этого вектора относительно точки А определит направление углового ускорения .
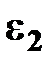| Первый этап |
| Второй этап |
| Третий этап |
| План ускорений структурной группы 2-3 |
| Pa |
| a |
| // x-x |
| anA |
| A1 |
| B1 |
| S2 |
| w1 |
| O |
| w2 |
| x |
| x |
| j1 |
| e1 |
| n1 |
| atA |
| n1 |
| atA |
| anA |
| a |
| n2 |
| // AB |
| anBA |
| n1 |
| atA |
| anA |
| a |
| n2 |
| anBA |
| ^ AB |
| n1 |
| atA |
| anA |
| a |
| n2 |
| anBA |
| b |
| atBA |
| aB |
| atBA |
| e2 |
| Pa |
| Pa |
| Pa |
| S2 |
| aS2 |
| // x-x |
| b |
Рис.6.1. Построение плана ускорений структурной группы 2-3
Для нахождения ускорения центра тяжести S2 звена AB необходимо определить полное ускорение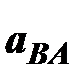 
, соединив при этом точки а и b на плане ускорений. Используя отношение
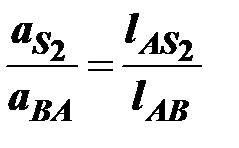или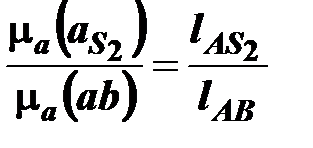 
Откуда определяется
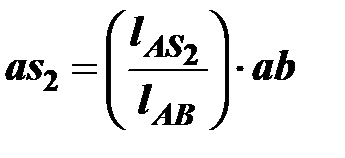
На плане ускорений откладываем отрезок аs2 и соединяем полученную точку s2 с полюсом pa. Отрезок pas2 изобразит на плане ускорение аS2
.
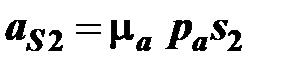Определяем ускорения структурной группы 4-5. ускорение точки С представляет собой векторную сумму ускорений
,
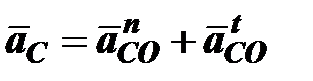где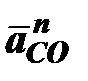 
– нормальное ускорение точки С вокруг точки О;
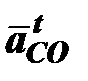– тангенциальное ускорение точки С вокруг точки О.
Нормальное ускорение определяется по формуле
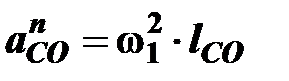м/с2,
где 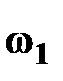– угловая скорость кривошипа в рассматриваемом положении, с-1, табл. 5.11;
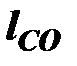– длина кривошипа, м.
Ускорение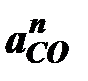 
направлено вдоль звена ОС к центру вращения точке, т.е. от точки С к точке О (рис. 6.1).
Касательное ускорение вычисляется по уравнению
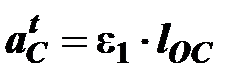м/с2,
где 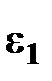– угловое ускорение кривошипа в рассматриваемом положении, с-2 , формула (6.1).
Рис.6.2. План ускорений механизма
Величина отрезка, который представляет на плане ускорений ускорение 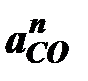вычисляется как
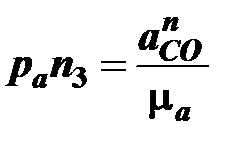мм,
Отрезок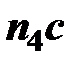 
, который изображает на плане ускорений, ускорение 
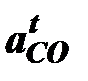рассчитывается по формуле
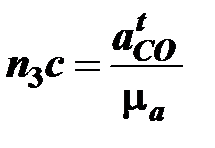мм.
Для определения ускорения точки D воспользуемся уравнением Эйлера
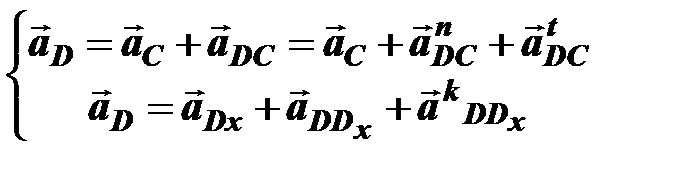(6.3)
где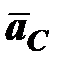 
– переносное ускорение точки C;
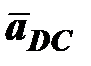– относительное ускорение точки D вокруг C, это ускорение раскладывается на две составляющие – 
,
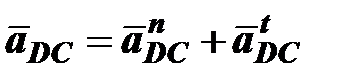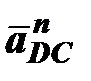– относительное нормальное ускорение точки D вокруг точки C, оно известно по абсолютной величине и по направлению: направлено параллельно звену CD, от точки D к точке C (т.D ®т.C) (рис.6.2), численное значение этого ускорения вычисляется по равенству
,
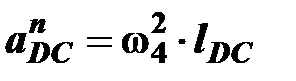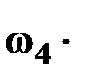– угловая скорость звена 4,указана в табл. 4.1.
На плане ускорений ускорение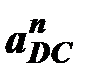 
отображается в виде отрезка 
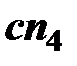, величина которого равна
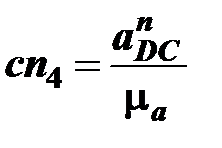мм;
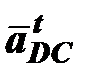– относительное тангенциальное ускорение точки D вокруг точки C, оно неизвестно по абсолютной величине и известно по направлению: направлено перпендикулярно звену CD;
aDх – ускорение точки в переносном вращательном движении с направляющей х-х, аDх=0;
аDDх – ускорение точки D в поступательном движении относительно точки Dх, оно направлено параллельно оси х-х;
акDDх – относительное кориолисово ускорение, акDDх=0.
Построение плана ускорений структурной группы 4-5 производится аналогично плану ускорений структурной группы 4-5. На основании построенного плана получили значения ускорений
,
,
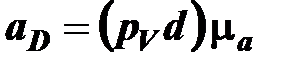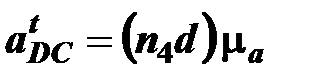и углового ускорения звена 4
.
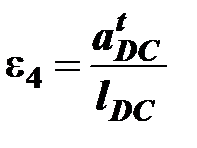Чтобы определить направление углового ускорения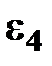 
, следует мысленно разметить вектор 
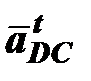в точку D. Направление вращения этого вектора относительно точки C определит направление углового ускорения 
.
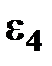Для нахождения ускорения центра тяжести S4 звена CD необходимо определить полное ускорение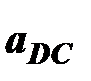 
, соединив при этом точки c и d на плане ускорений. Используя отношение
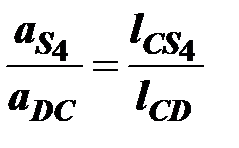или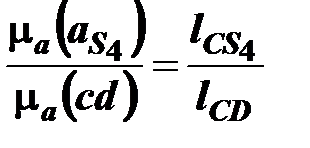 
.
Откуда определяется
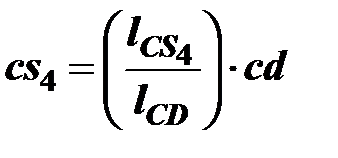мм.
На плане ускорений откладываем отрезок сs4 и соединяем полученную точку s4 с полюсом pa. Отрезок pas4 изобразит на плане ускорение аS4
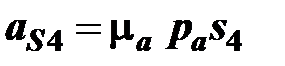м/с2.
Задачи силового расчета
Задачей силового расчета является определение реакций в кинематических парах механизма и внешней уравновешивающей силы (уравновешивающего момента).
Чтобы выполнить силовой расчет, необходимо определить внешние силы и моменты, действующие на звенья механизма – движущие силы, силы полезного сопротивления, силы тяжести. Реакции в кинематических парах вызываются не только действием внешних сил, но и силами инерции звеньев, которые двигаются с ускорениями. Если силовой расчет проводится с учетом сил инерции, то такой расчет называют кинетостатическим.
В основе кинетостатического метода расчета лежит принцип Д’Аламбера, который формулируется так: если к внешним силам, действующих на механическую систему можно рассматривать как условно находящуюся в равновесии. Иными словами, этот принцип дает возможность использовать уравнения равновесия для определения реакций в подвижных системах, т.е. уравнения статистки используются для задач динамики.
Силовой расчет проводится в соответствии со структурным анализом механизма – для всех структурных групп и исходного механизма. Силовой расчет начинается с наиболее удаленной от исходного механизма структурной группы.
В механизме (рис. 6.3) выделяются структурные группы 2-3 и 4-5 и исходный механизм. Действие отброшенных крайних кинематических пар заменяется действие реакций: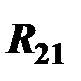 
, 
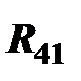, – вращательных А и С, 
, 
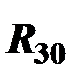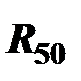– поступательных Bx, Dx.
Обозначение реакций, например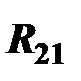 
, указывает – реакция, которая действует на звено 2 со стороны звена 1; или 
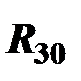– реакция, которая действует на звено 3 со стороны звена 0 (неподвижной стойки).
Рис.6.3. Реакции, которые возникают в механизме под действием внешних сил и сил инерции