Принятие решений в условиях риска

При принятии решений в условиях риска численные значения вероятностей исходов возможных решений известны. Исходная таблица, которую называют также «платежной матрицей», отличается от таблицы 5.1. одной строкой, в которой задается вероятность реализации каждого возможного состояния природы (таб. 5.2). Платежная матрица является матрицей либо возможных доходов (выигрышей), либо возможных потерь.

Таблица 5.2. Исходная матрица в условиях риска
			…
			…
			…
…	…	…	…	…
			…
			…

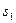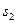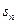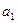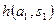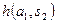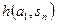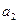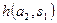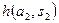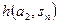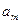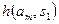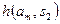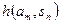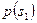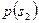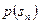Здесь 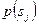— вероятность реализации состояния .

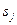Решение может приниматься на основе различных критериев, из которых мы рассмотрим основные:

- критерий ожидаемого значения,

- критерий дисперсии ожидаемого значения.

Критерий ожидаемого значения рассчитывается с использованием математического ожидания, которое в экономических задачах трактуется часто как ожидаемое среднее. Оно рассчитывается для каждого решения либо для доходов, либо для возможных потерь по формуле:

.

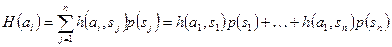Тогда задачу принятия решения в условиях риска можно рассматривать как задачу максимизации ожидаемого дохода 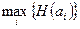или минимизации возможных потерь .

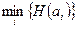Критерий дисперсии ожидаемого значения рассчитывается с использованием дисперсии, так как мерой ожидаемого риска в экономических задачах является дисперсия или среднее квадратическое отклонение, которое вычисляется, как корень из дисперсии.

Дисперсия полезности решения вычисляется по формуле:

.

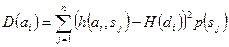Тогда задачу принятия решения в условиях риска можно рассматривать как задачу минимизации дисперсии ожидаемого значения .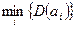

Рассмотрим конкретный пример.

Пример Т560. Предположим, что вы хотите вложить на фондовой бирже 10000 долл. в акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20%. Компания В обеспечивает безопасность инвестиций с 15% прибыли в условиях повышения котировок на бирже и только 5% — в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% — понижение котировок. В какую компанию следуют вложить деньги?

Возможные решения, которые можно принять:

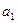— покупать акции компании А;

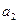— покупать акции компании В.

Возможные состояния внешней среды:

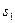— условия фондовой биржи будут благоприятны;

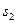— условия фондовой биржи будут неблагоприятны.

Рассчитаем ожидаемый доход при различных исходах.

Оценка исхода при повышении котировок, если деньги вложить в компанию А, равна 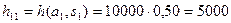, то есть прибыль составит 5000 долл. Если же деньги вложить в компанию В, прибыль составит 1500 долл., 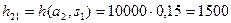долл.

В условиях понижения котировок, если деньги были вложены в компанию А, сумма инвестиции может обесцениться на 20%, следовательно 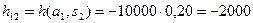, то есть прибыль составит 5000 долл. Если же деньги вложить в компанию В, прибыль составит 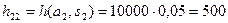долл.

Платежная матрица для этой задачи имеет вид:

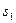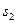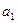		-2000
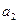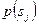	0,6	0,4

1. Рассмотрим критерий ожидаемого значения:

.

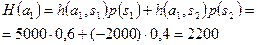
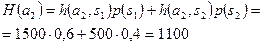
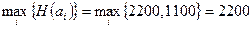По критерию ожидаемого значения оптимальным решением является покупка акций компании А, с ожидаемой полезностью 2200 долл.

2. Рассмотрим критерий дисперсии ожидаемого значения:

,

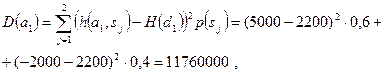
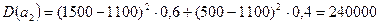По критерию дисперсии ожидаемого значения покупка акций компании А является более рискованной. Рассчитаем среднее квадратическое отклонение, оно является более наглядной мерой риска, так как имеет те же единицы измерения, что и исследуемая величина: 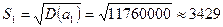долл.

Таким образом, хотя ожидаемая полезность от решения 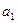максимизирует прибыль, в то же время это решение является более рискованным.

Метод дерева решений

Принятие решения в условиях риска может быть осуществлено методом дерева решения, который наглядно демонстрирует процесс принятия решения. Обычно деревья решений применяются для моделирования многоэтапных процессов принятия решений, в которых взаимосвязанные решения принимаются последовательно. Такое представление облегчает описание процесса принятия решений.

Метод состоит в построении специальной схемы. «Дерево» решений имеет «ствол», «ветви» и «узлы». «Ветви» обозначают возможные альтернативные решения, которые могут быть приняты, и возможные исходы, возникающие в результате этих решений. Квадратные «узлы» обозначают места, где принимается решение, круглые «узлы» — появление исходов [7].

Сначала дерево строится в прямом направлении, слева направо, начиная со ствола, который называют также «корнем». При этом вносятся известные числовые характеристики.

Затем проводится оценка дерева, этот этап реализуется в обратном направлении. Здесь вычисляются математические ожидания исходом и оценки лучших альтернатив.

И, наконец, дерево просматривается еще раз в прямом направлении для нахождения оптимального решения.

Дерево решений для примера Т560 будет иметь вид (рис. 5.1).

Из вершины 1 выходят две ветви, связанные с альтернативами выбора покупки акций. Каждый из узлов 2 и 3 делится далее тоже на две ветви, которые соответствуют случаям повышения или понижения котировок на бирже.

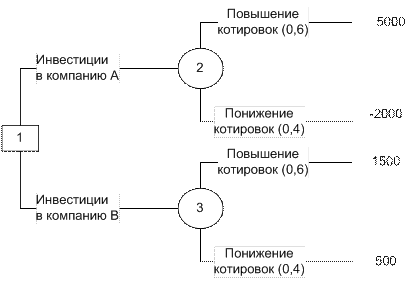
Рис. 5.1. Дерево решений

Исходя из схемы выбираем решение – покупка акций компании А.

Список литературы

1. Акулич И.Л. Математическое программирование в примерах и задачах: СПб.: Изд. Лань, 2011.

2. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. СПб.: Изд. Лань, 2000.

3. Горелик В.А. Исследование операций и методы оптимизации. М.: Изд. Академия, 2013.

4. Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Изд. Айрис-Пресс, 2002.

5. Киселева И.А. Моделирование рисковых ситуаций: Учебно-практическое пособие / Евразийский открытый институт. – М.: МЭСИ, 2007. – 102 с.

6. Таха Х. Введение в исследование операций. М.: Изд. Дом «Вильямс», 2005.

7. Эддоус М, Стэнсфилд Р. Методы принятия решений. – М., ЮНИТИ, 1997.

Оглавление

Предисловие. 1

Введение. 2

Глава 1. Линейное программирование. 3

1.1. Постановка задач линейного программирования. 3

1.2. Графический метод решения задач. 9

линейного программирования. 9

1.3. Графический анализ на чувствительность. 17

1.4. Симплекс-метод. 31

1.5. Двойственность в задачах. 41

линейного программирования. 41

1.6. Задачи для самостоятельно решения. 48

Глава 2. Транспортная задача. 49

2.1. Постановка транспортной задачи. 49

2.2. Нахождение начального допустимого плана. 51

2.3. Метод потенциалов для сбалансированной задачи. 58

2.5. Вырожденный план. 68

2.4. Задачи для самостоятельного решения. 70

Глава 3. Целочисленное программирование. 71

3.1. Задача о назначении. 71

3.2. Задача коммивояжера. 78

3.3. Задачи для самостоятельного решения. 89

Глава 4. Нелинейное программирование. 91

4.1. Основные понятия. 91

4.2. Постановки задачи нелинейного программирования. 94

4.3. Задача выпуклого программирования. 97

4.4. Метод кусочно-линейной аппроксимации. 100

Глава 5. Принятие решений в условиях. 104

неполной информации. 104

5.1. Принятие решений в условиях. 104

стохастической неопределенности. 104

5.2. Принятие решений в условиях риска. 110

5.3. Метод дерева решений. 113

Список литературы. 114