Понятие о двойственных задачах линейного программирования
С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. При этом первоначальная задача называется исходной.
| Исходная задача | Двойственная задача |
| Стандартная форма записи | |
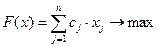 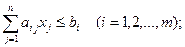 (4.1) (4.1) 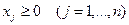 . . | 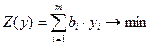 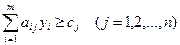 ; (4.2) ; (4.2) 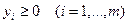 . . |
| Каноническая форма записи | |
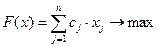 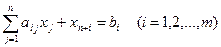 ; (4.3) ; (4.3) 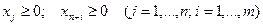 . . | 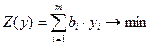 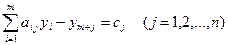 ; (4.4) ; (4.4) 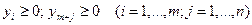 . . |
| Оптимальное решение | |
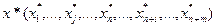 . . | 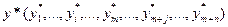 . . |
Связь исходной и двойственной задач состоит в том, что
1) коэффициенты 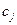 целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи;
целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи;
2) свободные члены 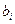 системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи;
системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи;
3) матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи;
4) одна из взаимно двойственных задач на максимум, а другая на минимум.
Между оптимальными решениями взаимно двойственных задач существует определенная связь, которая может быть установлена с помощью теорем двойственности и следствий к ним. Приведем некоторые из них.
Первая теорема двойственности. Если одна из взаимно двойственных задач ЛП имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их целевых функций равны: 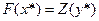 (
( 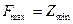 ).
).
Если целевая функция одной из задач не ограничена, то условия другой задачи противоречивы.
Установим взаимнооднозначное соответствие между переменными взаимно двойственных задач в виде следующей схемы:
| Переменные исходной задачи | |
| Первоначальные переменные | Балансовые переменные |
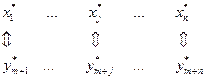 | 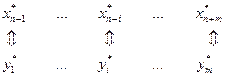 |
| Балансовые переменные | Первоначальные переменные |
| Переменные двойственной задачи |
Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Следствие ко второй теореме двойственности. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи:
1) если 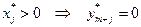 или
или 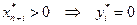 ;
;
2) если 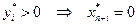 или
или 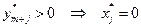 .
.
Следствие к третьей теореме двойственности: i-ую компоненту оптимального решения двойственной задачи 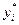 можно найти из равенства
можно найти из равенства 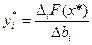 , где
, где 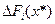 - это изменение оптимального значения целевой функции исходной задачи, вычисленное в предположении, что правая часть i-го ограничения изменилась на
- это изменение оптимального значения целевой функции исходной задачи, вычисленное в предположении, что правая часть i-го ограничения изменилась на 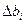 единиц. Равенство справедливо только для достаточно малых значений
единиц. Равенство справедливо только для достаточно малых значений 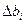 .
.
Задача №4.1.
Построить и решить с использованием теории двойственности задачу двойственную задаче №1.1.
Решение.
Таблица с данными к задаче №1.1
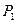 | 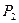 | запасы | |
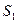 | |||
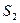 | |||
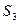 | |||
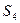 | |||
| доход |
| Исходная задача | Двойственная задача |
| Стандартная форма записи | |
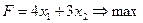 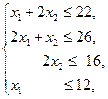 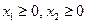 . (4.5) . (4.5) | 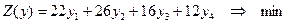 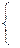 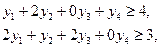 (4.6) (4.6) 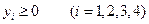 . . |
| Каноническая форма записи | |
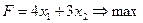 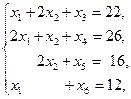 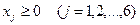 . . | 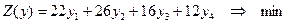 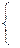 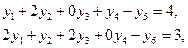 (4.7) (4.7) 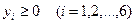 . . |
Согласно первой теореме двойственности 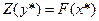 , так как
, так как 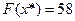 , то
, то 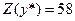 .
.
Установим взаимнооднозначное соответствие между переменными взаимно двойственных задач в виде схемы:
| Переменные исходной задачи | |
| Первоначальные переменные | Балансовые переменные |
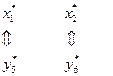 | 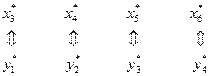 |
| Балансовые переменные | Первоначальные переменные |
| Переменные двойственной задачи |
Для нахождения компонент оптимального решения двойственной задачи, воспользуемся решением исходной задачи 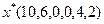 , полученным в задаче № 3.1
, полученным в задаче № 3.1
Так как 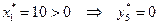 ;
;
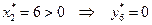 ;
;
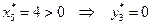 ;
;
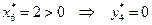 .
.
Подставляя в систему ограничений (4.7) нулевые значения переменных 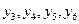 , получим систему:
, получим систему: 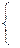
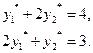 Решив, которую, найдем недостающие компоненты оптимального решения двойственной задачи:
Решив, которую, найдем недостающие компоненты оптимального решения двойственной задачи: 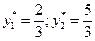 .
.
Оптимальное решение двойственной задачи имеет вид 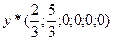 .
.
Замечание. Задача №1.1 и двойственная задача к задаче № 1.1 были решены симплексным методом в §3. Для того, чтобы убедиться в справедливости второй теоремы двойственности выпишем выражения целевых функций через свободные переменные на последнем шаге и
решения этих задач
| Исходная задача | Двойственная задача |
| Целевая функция на последнем шаге | |
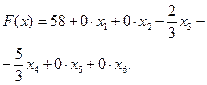 | 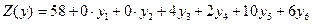 . . |
| Оптимальное решение | |
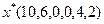 . . | 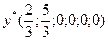 . . |
Компоненты оптимального решения двойственной задачи 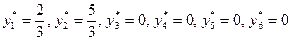 равны коэффициентам при соответствующих переменных целевой функции прямой задачи, взятым по абсолютной величине. Аналогично, компоненты оптимального решения прямой задачи
равны коэффициентам при соответствующих переменных целевой функции прямой задачи, взятым по абсолютной величине. Аналогично, компоненты оптимального решения прямой задачи 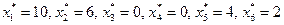 равны коэффициентам при соответствующих переменных целевой функции двойственной задачи, взятым по абсолютной величине.
равны коэффициентам при соответствующих переменных целевой функции двойственной задачи, взятым по абсолютной величине.
