Конвективный теплообмен

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Конвективный теплообмен — это процесс передачи теплоты между твердой поверхностью и окружающей средой, который осуществляется через ламинарный пограничный слой, образующийся в любом случае; в остальном объеме перенос теплоты осуществляется конвекцией. Различают два вида конвекции: свободную (естественную) и вынужденную. При свободной конвекции жидкость движется за счет разности плотностей, при вынужденной - под действием внешних сил (насос, вентилятор, ветер). Основным уравнением конвективного теплообмена в любом случае является уравнение Ньютона, сводящееся к утверждению, что количество теплоты пропорционально площади поверхности Н и разности температур ∆t:

где а - коэффициент пропорциональности (коэффициент теплоотдачи), Вт/(м² • К), характеризующий величину удель­ного теплового потока, передаваемого единицей поверхности при градиенте в 1 град.

Коэффициент теплоотдачи можно представить в виде

где ∆ - толщина ламинарного пограничного слоя.

В этом случае оказывается, что 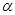зависит от большого числа факторов - аналогично ∆ и не имеет аналитического решения. Определяют коэффициент теплоотдачи эксперимен­тально, и это сообщает всему учению о конвективном тепло­обмене эмпирический характер. Применение теории подобия и теории размерностей дает возможность обобщить опытные данные и свести задачу конвективного теплообмена к зависи­мости параметров гидродинамического и теплового подобия, в результате чего учение о конвективном теплообмене приобре­тает полуэмпирический характер.

ТЕОРИЯ РАЗМЕРНОСТЕЙ

Теория размерностей используется в том случае, когда нет дифференциального уравнения, описывающего данный про­цесс. В условиях вынужденной конвекции коэффициент тепло­отдачи является функцией по крайней мере шести независи­мых переменных: весовой скорости и, кг/(м² • с); линейного размера l; вязкости 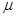, кг/(м² • с); теплоемкости С, Дж/(кг • К);

плотности 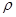, кг/м³; теплопроводности 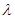, Вт/(м • К). При экспериментальном определении 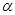, Вт/(м² • К), необходимо исследовать зависимость этого коэффициента от этих пере­менных и провести число опытов N = А 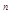, где A - число опытов с одной переменной, например, A= 10;

n - число независимых переменных. Для данного примера оказывается:

число опытов равно одному миллиону, что совершенно не­реально. Применение же теории размерностей приводит к сокращению независимых переменных. В условиях вынужден­ной конвекции коэффициент теплоотдачи является функцией:

Полный дифференциал а равен

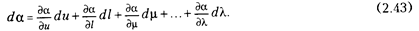
Для перехода к безразмерным (относительным) величинам необходимо иметь переменные, не отсчитываемые от постоян­ного "нулевого" уровня. Разделим полученное уравнение на а и одновременно разделим и умножим каждое слагаемое на соответствующие значения l/l;u/u; 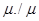и т.д. Тогда

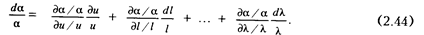
Считаем, что соотношение частных производных является постоянным:

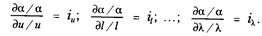
Тогда получим

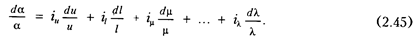
Проинтегрируем полученное выражение:

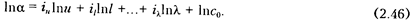
После потенциирования получим:

Необходимым условием общности полученного решения должно быть требование безразмерности постоянной 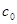или ее обратной величины:

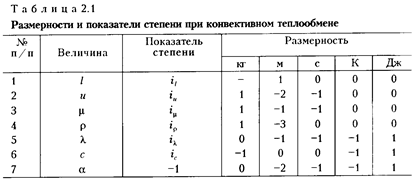
Это уравнение не зависит от системы единиц; в связи с тем, что 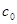является безразмерной величиной, все единицы из­мерений (справа) должны входить в это уравнение в нулевой степени. Для исключения размерностей составим табл. 2.1.

Исключаем размерности:

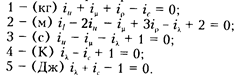
Как видно из двух последних уравнений, полученных исключением размерности, они тождественны, так как связаны с определением теплоемкости воды. Таким образом, имеем четыре независимых уравнения связи при шести независимых переменных.

Следовательно, в исходной системе уравнений только два неизвестных показателя подлежат эксперименталь­ному определению, а остальные вычисляются по полученной системе уравнений в зависимости от этих двух основных. Например, в опыте определены показатели, которые соответст­венно равны: 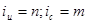; (п, т - число). Тогда, используя систему уравнений, получим:

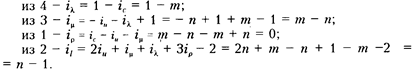
Подставив полученные значения показателей, получим

Преобразуем полученные уравнения, сгруппировав величины с одинаковыми показателями:

где 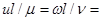Re - критерий Рейнольдса - критерий гидродинамического подобия; 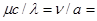Pr - критерий Прандтля - критерий теплофизического подобия; + 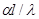= Nu - критерий Нуссельта - критерий теплового подобия.

Таким образом, на основании теории размерностей получе­но уравнение связи безразмерных параметров, характеризующих

теплообмен в условиях вынужденной конвекции, и число независимых переменных снижено с 6 до 2, что обеспечивает возможность их экспериментального определения, и тогда N = А 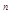= 100.

Правильность использования теории размерностей под­тверждается 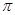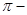теоремой. Исходя из этого физическое уравне­ние, содержащее п 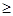1 размерных величин, из которых т 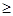1 имеют независимые размерности, после приведения их к безразмерному виду должно содержать v безразмерных параметров: 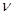= п - т. В нашем случае 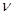= n – m = 6 – 4 = 2. Численные значения входящих в уравнение постоянных 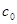, п и т определяются экспериментально и в зависимости от вида теплообмена приводятся в справочной литературе (некоторые даны в табл. 4.4).

ТЕОРИЯ ПОДОБИЯ

При использовании теории подобия необходимо иметь диф­ференциальное уравнение, описывающее исследуемый про­цесс. Проводя критериальную обработку этого уравнения, получают состав критериев подобия. Выявление состава критериев подобия осуществляется методом "губки": в исход­ном дифференциальном уравнении опускают знаки дифферен­циалов, полученные результаты приравнивают и выделяют независимые слагаемые, на основании которых определяют параметры подобия.

Для конвективного теплообмена (его математического описания) необходимо иметь: 1) дифференциальное уравнение движения вязкой несжимаемой жидкости - уравнение Навье - Стокса; 2) уравнение теплопроводности Фурье - Кирхгофа;

3) уравнение теплообмена на границе твердая поверхность - окружающая среда — уравнение Био — Фурье.

Уравнение движения вязкой несжимаемой жидкости

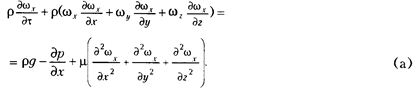
На основании теории подобия с использованием метода "губки" получаем пять независимых комплексов. Уравнение записано для одномерного потока по оси х.

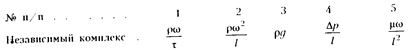
Группируем полученные независимые комплексы и по­лучаем критерии подобия:

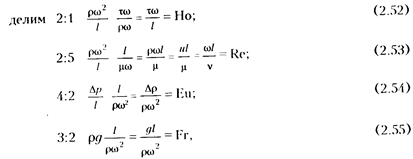
где Но - критерий гомохронности - гидродинамический крите­рий одновременности событий; Re - критерий Рейпольдса-параметр гидродинамического подобия режимов движения жидкости, характеризующий соотношение сил инерции и сил вязкости; Eu - критерий Эйлера, характеризующий соотноше­ние сил и инерции и сил давления; Fr - критерий Фруда, характеризующий соотношение сил инерции и сил тяжести.

Следует отметить, что полученный оспенной состав крите­риев подобия Но, Re, Fu, Fr характеризует режим движения потока и может быть преобразован в любой иной состав критериев подобия умножением или делением исходного состава, но при этом в любом случае должно выполняться условие возврата любого иною состава критериев подобия к исходному.

Так, вместо критерия Фруда можно использовать критерий Гали лея

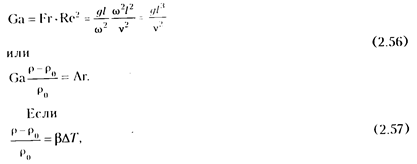
Умножив критерии Ga на относительное изменение плот­ности

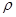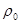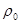( - )/ ,получим критерий Архимеда Аг. Если ( 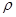- 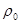)/ 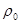= 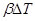происходит за счет разности температур 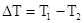то получим критерий Грасгофа Gr. Критерий Аг характеризует значение подъемной силы при изучении свободной конвекции жидкости, в которой находятся пузырьки, твердые частицы или капли другой жидкости. Критерий Ga используется вместо критерия Fr, так как в него входит скорость потока, которую трудно измерить.

Кроме того, оказывается, что часть критериев является зависимой, т.е. функцией других критериев. Так, критерий Ей зависит от Re, что подтверждается при рассмотрении уравне­ния Дарси - Вейсбаха

откуда

с другой стороны,

Вторым уравнением, описывающим процесс конвективного теплообмена при вынужденном движении, является уравнение теплопроводности

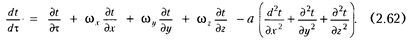
Применяя метод "губки", получим три независимых комп­лекса.

Делим:

второй на третий

третий на первый

Получаем критерии Пекле Ре и Фурье Fo. Критерий Ре характеризует соотношение тепловых потоков, переносимых конвекцией и теплопроводностью. Вместо критерия Ре можно использовать критерий Прандтля, так как

Критерий Fo характеризует одновременность событий, так называемое безразмерное время. Из третьего уравнения тепло­обмена на границе твердая поверхность - окружающая среда получим критерий теплового подобия - критерий Нуссельта Nu.

Таким образом, проведя критериальную обработку диффе­ренциальных уравнений, получим состав критериев подобия:

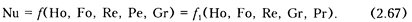
Связь между критериями определяется опытным путем. Следует заметить, что теории размерностей и подобия могут использоваться при изучении любых процессов (гидравли­ческих, механических, экономических).

В табл. 2.2 приводятся некоторые критерии тепловых и гидродинамических процессов.

Критериальные уравнения. При установлении функцио­нальной связи между коэффициентом теплоотдачи и пара­метрами конвективного теплообмена можно перейти от раз­мерных функций к безразмерным и, используя эксперимент, определять функции типа

Формула называется критериальным уравнением. Количест­во переменных (которыми здесь являются критерии подобия),

входящих в такую зависимость, всегда значительно меньше, чем в случае установления зависимости в размерном виде. Имея конкретный вид функции, легко определить значение коэффициента теплоотдачи. Вычисление критериев подобия Re, Pr, Gr и др. не представляет значительных трудностей.

Практическое использование критериальных уравнений в тепловых расчетах ДВС заключается в определении с их помощью коэффициента теплоотдачи

Некоторые случаи теплообмена. Применительно к опре­деленным задачам уравнение может быть упрощено. При стационарных процессах теплообмена выпадают критерии Fo. Но и тогда

В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому уравнение подобия тепло­отдачи упрощается:

Для некоторых газов значение числа Прандтля Pr в про­цессе конвективного теплообмена почти не изменяется с темпе­ратурой, поэтому уравнение подобия принимает более простой

вид:

При свободном движении жидкости, когда вынужденная конвекция отсутствует, вместо числа Рейнольдса в уравнение подобия теплоотдачи необходимо ввести число Грасгофа:

Итак, теория подобия позволяет, не интегрируя дифферен­циальных уравнений, получить из них критерии подобия и установить критериальные зависимости, которые справедливы для всех подобных между собой процессах. Однако следует помнить, что такие обобщенные зависимости ограничены усло­виями подобия, из них нельзя делать заключения, выходящие за пределы этих ограничений. Общего решения теория подо­бия не дает: она позволяет лишь обобщить опытные данные в области, ограниченной условиями подобия. При использовании метода подобия об этих ограничениях всегда нужно помнить.

Расчетные зависимости конвективного теплообмена. В

качестве конкретной формы расчетных уравнений обычно при­нимается степенная зависимость

Она наиболее простая и гибкая. Подробно математическая обработка результатов экспериментов рассматривается в спе­циальной литературе. Ограничимся рассмотрением лишь не­которых вопросов конвективного теплообмена, встречающихся при тепловых расчетах агрегатов ДВС.

Установившийся конвективный теплообмен в общем случае описывается следующим уравнением подобия (капельной жид­кости):

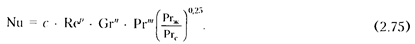
Введение множителя ( 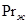/ Pr 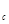) 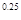в уравнение подобия для капельных жидкостей дает возможность использовать эти уравнения при любом направлении теплового потока (от стенки к среде и наоборот) и учесть изменение теплофизи-ческих свойств среды. Индексы "ж" и "с" означают, что теплофизические параметры жидкости следует выбирать при средней ее температуре и соответственно при средней темпе­ратуре стенки.