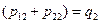Вопрос 16. Математическое ожидание дискретной случайной величины и его свойства

Вопрос 15. Геометрическое и гипергеометрическое распределения.

Геометрическое распределение.

Производится неограниченное количество испытаний до тех пор пока не произойдёт событие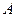

p – постоянна

1-p – вероятность непоявления события

X – количество проведенных испытаний

X = 1,2,3…

X					…	k	…
p	p	qp	q2p	q3p		qk-1p

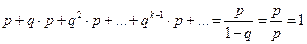бесконечно убывающая геометрическая прогрессия

Случайная величина, распределённая по этому закону называется геометрическим распределением.

_____________________

Пример:

5 выстрелов

p=0,8 n=5

составим закон распределения случайной величины, равной произведению выстрелов

X
p	0,8	0,2∙0,8	0,22∙0,8	0,23∙0,8	0,24∙0,8

______________________

Гипергеометрическое распределение.

N - всего изделий M – бракованные изделия

K - выбирается

Определить вероятность что из них l окажется бракованных.

Всего возможных способов выбрать K из N:

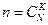
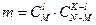
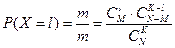
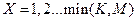
Случайная величина распределенная по этому закону называется гипергеометрическим распределением.

Вопрос 16. Математическое ожидание дискретной случайной величины и его свойства.

Математическое ожидание. Его свойства.

X	X1	X2	…	Xn
p	p1	p2	…	pn

Математическим ожиданием дискретной случайной величины называется сумма произведений ее значений на соответствующие вероятности.

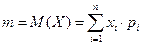
Пример:

Найти математическое ожидание числа появлений событий A в одном испытании если вероятность этого события в каждом из испытаний равна p.

X – число появления событий A в одном испытании.

X
p	1-p	p

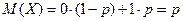
Математическое ожидание числа появления события в 1ом испытании равно вероятности этого события.

Св-ва математического ожидания:

X	C
p	1

1)

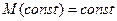
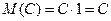
2)

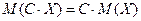
Произведение случайной величины на число C

под произведением понимается случайная величина 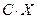, которая может принимать все возможные значения случайной величины 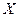, умноженной на константу .

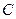X	X1	X2	…	Xn
p	p1	p2	…	pn

СX	СX1	СX2	…	СXn
p	p1	p2	…	pn

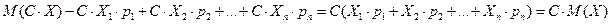
3) Определ. произведение случайных величин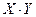

если	Xзнач	X1	X2
а	Yзнач	Y1	Y2

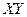
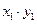
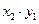
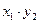
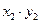
Независимые случайные величины – если соответствующая вероятность одной случайной величины не зависит от того какое значение приняла другая случайная величина.

Если случайные величины независимы, то математическое ожидание их произведения равно произведению их математических ожиданий.

Y	y1	y2
p	q1	q2

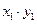
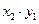
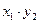
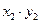
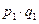
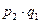
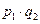
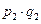
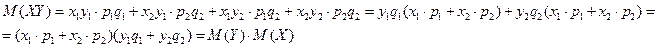
4) Случайные величины X и Y определяют сумму случайных величин как некоторую величину 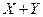, которая может принимать все возможные значения сумм.

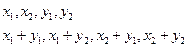Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий. Справедливо как для зависимых так и независимых величин.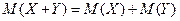

X	x1	x2
p	p1	p2

X+Y	x1+y1	x1+y2	x2+y1	x2+y2
p	p11	p12	p21	p22

Y	y1	y2
p	q1	q2

Вероятности могут принимать различные значения, в зависимости от того будут случайные величины зависимыми или независимыми.

- В случае независимых случайных величин соответствующие вероятности перемножаются.

- В случае зависимых случайных величин вероятность того, что случайная величина 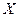приняла значение 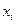умножаем на соответствующую условную вероятность того что 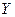приняла значение .

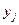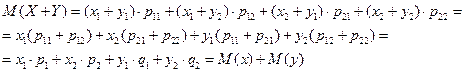
Рассмотрим в отдельности каждую скобку

; ; ;
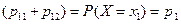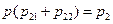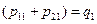