Реальное дифференцирующее звено
(Слайд 39)
Звено описывается уравнением
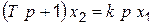 . (4.48)
. (4.48)
Передаточная функция звена
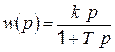 . (4.49)
. (4.49)
Звено условно можно представить в виде двух включенных последовательно звеньев – идеального дифференцирующего звена и апериодического звена первого порядка.
(Слайд 40)
На рис. 4.21 изображены примеры реальных дифференцирующих звеньев: дифференцирующая RC-цепь (рис. 4.21, а), RL-цепь (рис. 4.21, б) и дифференцирующий трансформатор (рис. 4.21, в).

Рис. 4.21. Реальные дифференцирующие звенья
(Слайд 41)
Переходная функция определяется решением (4.48) при х1 = 1(t) и нулевых начальных условиях
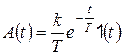 . (4.50)
. (4.50)
Функция веса
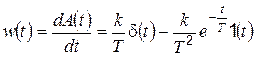 . (4.51)
. (4.51)
(Слайд 42)
Временные характеристики изображены на рис. 4.22. Там же показаны построения, позволяющие по экспериментальным характеристикам определять параметры звена.
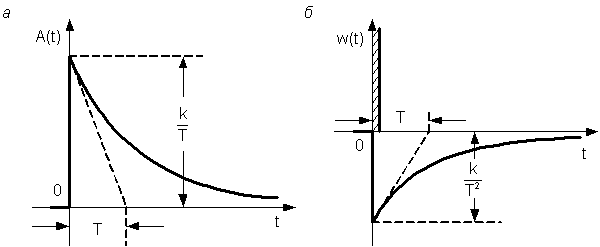
Рис. 4.22. Переходная функция (а) и дельта-функция (б)
реального дифференцирующего звена
(Слайд 43)
Частотная передаточная функция, её модуль и фаза соответственно равны:
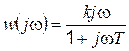 ; (4.52)
; (4.52)
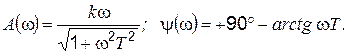 (4.53)
(4.53)
(Слайд 44)
Амплитудная, фазовая и амплитудно-фазовая характеристики звена изображены на рис. 4.23.
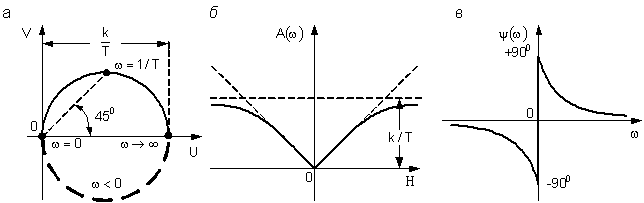
Рис. 4.23. АФЧХ (а), АЧХ (б) и ФЧХ (в) реального дифференцирующего звена
Амплитудная характеристика реального звена отличается от амплитудной характеристики идеального дифференцирующего звена (показана пунктиром). Характеристики совпадают в области низких частот. В области высоких частот реальное звено пропускает сигнал хуже, чем идеальное звено. Коэффициент передачи стремится к значению k / T при 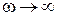 . Для звеньев, представляющих собой RC- или RL-цепь (см. рис. 4.21), коэффициент k / T = 1, и на высоких частотах коэффициент передачи стремится к единице.
. Для звеньев, представляющих собой RC- или RL-цепь (см. рис. 4.21), коэффициент k / T = 1, и на высоких частотах коэффициент передачи стремится к единице.
Это означает, что в дифференцирующей RC-цепи конденсатор имеет сопротивление, стремящееся к нулю, а в дифференцирующей RL-цепи индуктивность имеет сопротивление, стремящееся к бесконечности. И в том, и в другом случаях напряжение на выходе будет равно напряжению на входе.
Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при 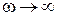 . Здесь также видно, что реальное звено ведет себя подобно идеальному только в области низких частот.
. Здесь также видно, что реальное звено ведет себя подобно идеальному только в области низких частот.
Амплитудно-фазовая характеристика для положительных частот представляет собой полуокружность с диаметром, равным k / T. На полуокружности нанесены характерные точки: 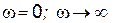 и
и 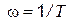 . Дополнив эту полуокружность её зеркальным изображением относительно вещественной оси, получим полную амплитудно-фазовую характеристику для всех частот, лежащих в пределах
. Дополнив эту полуокружность её зеркальным изображением относительно вещественной оси, получим полную амплитудно-фазовую характеристику для всех частот, лежащих в пределах 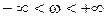 .
.
ЛАХ строится по выражению
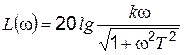 . (4.54)
. (4.54)
(Слайд 45)
Для построения асимптотической ЛАХ (рис. 4.24) проведем вертикальную линию при сопрягающей частоте 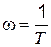 .
.
Левее этой линии, то есть при 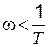 , можно воспользоваться приближенным выражением
, можно воспользоваться приближенным выражением 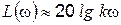 . Этому выражению соответствует прямая линия с положительным наклоном 20 дБ/дек (прямая а–b). Она может быть построена, например, по частоте среза
. Этому выражению соответствует прямая линия с положительным наклоном 20 дБ/дек (прямая а–b). Она может быть построена, например, по частоте среза 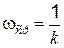 .
.
Для частот 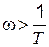 можно пользоваться приближенным выражением
можно пользоваться приближенным выражением 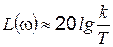 . Этому выражению соответствует прямая, параллельная оси частот (b – с). Действительная ЛАХ отличается от асимптотической в точке излома b на величину 3 дБ.
. Этому выражению соответствует прямая, параллельная оси частот (b – с). Действительная ЛАХ отличается от асимптотической в точке излома b на величину 3 дБ.
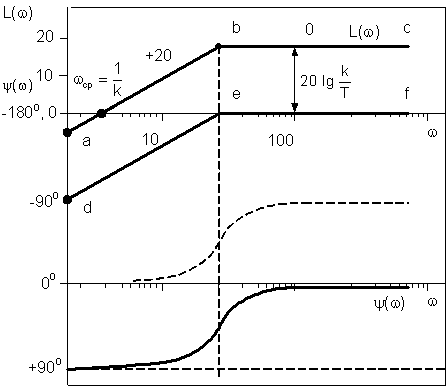
Рис. 4.24. ЛАХ и ЛФХ реального дифференцирующего звена
На рис. 4.24 показана асимптотическая ЛАХ для случая k = 1 (ломаная прямая d–e–f).
ЛФХ строится по второму уравнению системы (4.53). Для этого сначала строится первое слагаемое y1 = + 90°, а затем второе y2 = –аrctg wТ. Результирующая ЛФХ показана сплошной линией. При 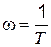 фазовый сдвиг равен + 45°.
фазовый сдвиг равен + 45°.
Неустойчивые звенья
Рассмотренные выше звенья позиционного типа относятся к устойчивым звеньям или звеньям с самовыравниванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся режиму при ограниченном изменении входной величины или возмущающего воздействия. Термин «самовыравнивание» обычно применяется для звеньев, представляющих собой объекты регулирования.
Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например звенья интегрирующего типа. Они были рассмотрены выше.
Существуют звенья, у которых этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или комплексных корней с положительной вещественной частью в характеристическом уравнении (в знаменателе передаточной функции, приравненном нулю), в результате чего звено относится к категории неустойчивых звеньев.
(Слайд 46)
Рассмотрим в качестве примера звено, описываемое дифференциальным уравнением вида
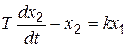 (4.55)
(4.55)
или
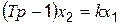 . (4.56)
. (4.56)
Этому дифференциальному уравнению соответствует передаточная функция
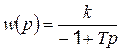 . (4.57)
. (4.57)
(Слайд 47)
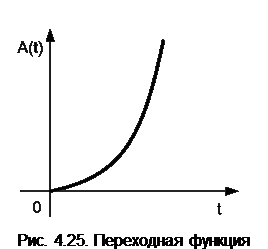 Переходная функция звена представляет собой показательную функцию с положительным показателем
Переходная функция звена представляет собой показательную функцию с положительным показателем
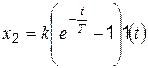 . (4.58)
. (4.58)
Эта характеристика изображена на рис. 4.25.
Таким звеном может быть, например, асинхронный двухфазный управляемый двигатель, если он имеет механическую характеристику с отрицательным наклоном.
Существенной особенностью неустойчивых звеньев является наличие больших по сравнению с устойчивыми звеньями фазовых сдвигов.
(Слайд 48)
Так, для рассмотренного выше апериодического звена с отрицательным самовыравниванием имеем частотную передаточную функцию
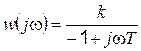 . (4.59)
. (4.59)
Модуль её не отличается от модуля частотной передаточной функции апериодического звена с положительным самовыравниванием (4.8)
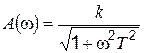 , (4.60)
, (4.60)
а фаза
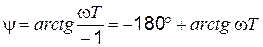 (4.61)
(4.61)
имеет большое значение по сравнению со вторым уравнением в (4.8).
В связи с этим неустойчивые звенья относят к группе так называемых неминимально-фазовых звеньев. К неминимально-фазовым звеньям относятся также устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью.
(Слайд 49)
Например, звено с передаточной функцией
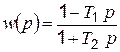 (4.62)
(4.62)
относится к группе неминимально-фазовых звеньев.
(Слайд 50)
К неустойчивым звеньям относится также ряд других звеньев, имеющих передаточные функции вида
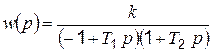 ; (4.63)
; (4.63)
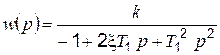 ; (4.64)
; (4.64)
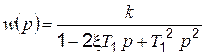 ; (4.65)
; (4.65)
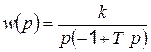 . (4.66)
. (4.66)
Наличие в автоматической системе неустойчивых звеньев вызывает некоторые особенности расчета.
