Физическое моделирование конвективного теплообмена

В данном разделе приведены уравнения конвективного теплообмена. Получена система уравнений конвективного теплообмена в безразмерном виде. Установлены уравнения подобия для процессов конвективного теплообмена. Рассмотрены условия моделирования конвективного теплообмена. Рассмотрена методика получения эмпирических уравнений подобия.

4.1 Уравнения конвективного теплообмена

При конвективном теплообмене имеет место перенос теплоты за счет движения жидкости из области с одной температурой в область с другой температурой, а также перенос теплоты теплопроводностью. Температурное поле движущейся жидкости при отсутствии внутренних источников теплоты описывается уравнением энергии [1]:

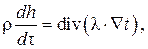(4.1)

где t = t(x,y,z,t) – температурное поле жидкости; x, y, z – декартовы координаты; t – время; r – плотность жидкости, кг/м³; l - коэффициент теплопроводности жидкости, Вт/(м×К); h – энтальпия жидкости, Дж/кг.

Поскольку dh = c_p×dt, где c_p – изобарная теплоемкость, то уравнение (4.1) в развернутом виде запишется так:

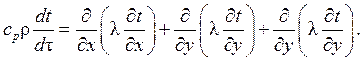(4.2)

Если коэффициент теплопроводности жидкости l является постоянным, то его можно вынести из под знака производной, и уравнение (4.2) примет вид:

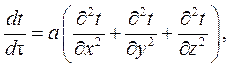(4.3)

где а - коэффициент температуропроводности жидкости: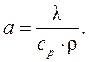

Полная производная dt/dt характеризует изменение температуры движущейся частицы жидкости со временем, ее можно записать в виде [1]:

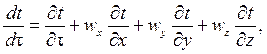(4.4)

где ¶t/¶t - частная производная, характеризующая изменение температуры в неподвижной точке в объеме жидкости; w_x, w_y, w_z – компоненты вектора скорости на декартовы оси.

С учетом (4.4) уравнение энергии (4.3) для процессов конвективного теплообмена запишется следующим образом:

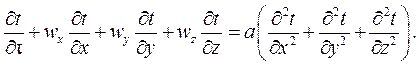(4.5)

Плотность теплового потока в движущейся жидкости за счет конвекции и теплопроводности можно рассчитать по выражению:

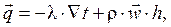(4.6)

где 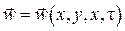- поле скоростей в рассматриваемом объеме жидкости, причем 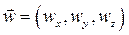. Слагаемое 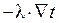описывает перенос теплоты за счет теплопроводности; слагаемое 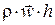описывает перенос теплоты конвекцией.

В случае неподвижной жидкости во всех ее точках 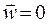, и уравнение (4.5) превращается в дифференциальное уравнение теплопроводности, которое используется для описания температурного поля твердых тел:

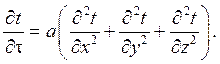
Выражение (4.6) при 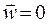принимает выражение закона Фурье:

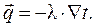(4.7)

При стационарных режимах конвективного теплообмена в каждой неподвижной точке области движущейся жидкости температура остается постоянной, т.е. ¶t/¶t = 0, тогда уравнение энергии (4.5) принимает вид:

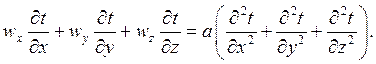(4.8)

Наибольший практический интерес представляет конвективный теплообмен между движущейся жидкостью и омываемой ею поверхностью твердого тела. Известно, что в случае сплошной среды на поверхности тела выполняются условия прилипания (3.13), т.е. на поверхности твердого тела w_x = w_y = w_z = 0. Иначе говоря, вблизи поверхности твердого тела образуется бесконечно тонкий слой неподвижной жидкости, перенос теплоты в котором происходит за счет теплопроводности по закону Фурье (4.7). Кроме того, частицы жидкости на поверхности твердого тела принимают температуру поверхности тела t_п:

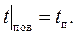(4.9)

На рис. 8 показана схема теплообмена между жидкостью и поверхностью твердого тела, где t - температурное поле жидкости; t¢- температурное поле твердого тела; w₀, t₀ - характерные скорость и температура жидкости; q_п - плотность теплового потока от поверхности тела к жидкости; t_п - температура поверхности твердого тела; n - направление нормали к поверхности тела.

Рис. 8. Схема теплообмена между жидкостью и поверхностью тела.

Плотность теплового потока от поверхности твердого тела к жидкости при конвективном теплообмене определяется законом Фурье, примененным к тонкому приповерхностному слою жидкости:

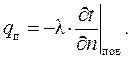(4.10)

При расчетах конвективного теплообмена часто используют конвективный коэффициент теплоотдачи на поверхности твердого тела, Вт/(м²×К), определяемый выражением:

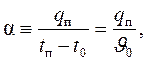(4.11)

где 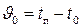- характерный температурный напор между поверхностью тела и жидкостью. Строго говоря, выражение (4.11) является корректным в том случае, когда температура поверхности t_п и температура жидкости t₀ одинаковы для всех точек поверхности. В противном случае нужно вводить средний температурный напор между поверхностью тела и жидкостью.

Подставляя величину q_п из (4.10) в (4.11), получим уравнение теплоотдачи:

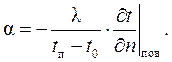(4.12)

Таким образом, уравнения конвективного теплообмена между жидкостью и поверхностью тела при стационарном режиме включают в себя уравнение энергии (4.8), и уравнение теплоотдачи (4.10) или (4.12). Поскольку в уравнение движения входят компоненты скорости w_x, w_y, w_z, то нужно добавить уравнения, описывающие движение жидкости: уравнения Навье-Стокса (3.4) или (3.8), и уравнение неразрывности (3.10).

Для описания конкретного процесса конвективного теплообмена нужно задать условия однозначности, включающие в себя:

1) геометрические условия: форма и характерные размеры омываемого твердого тела l, l₁, l₂,…;

2) физические условия: теплофизические параметры жидкости l, r, с_р, а, m, n, b;

3) граничные условия: скорости и температуры (или их производные) на границах изучаемого объема жидкости .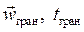

На поверхностях твердых тел скорость и температура жидкости принимается равной скорости и температуре поверхности твердого тела (выражения (3.13) и (4.9)). Кроме того, задаются распределения скорости и температуры жидкости на входе в изучаемую область, или на удалении от поверхности твердого тела.

4.2 Описание уравнений конвективного теплообмена

в безразмерном виде

Обычно практический интерес представляет конвективный теплообмен между жидкостью и омываемой ей поверхностью твердого тела. Как и в п. 3.2 введем безразмерные координаты, скорости и температуру:

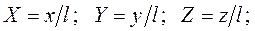
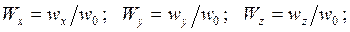
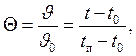
где l – характерный размер тела; w₀ – характерная скорость жидкости; 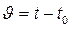– избыточная температура жидкости; 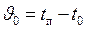– характерный температурный напор (t_п, t₀ – характерные температуры поверхности и жидкости).

Выразим размерные координаты, скорости и температуру:

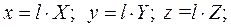
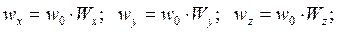(4.13)

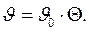
Очевидно, что уравнение энергии (4.8) можно записать в виде

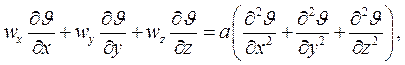
где вместо размерной температуры t выступает избыточная температура .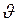

Подставляя выражения (4.13) в последнее уравнение, получим:

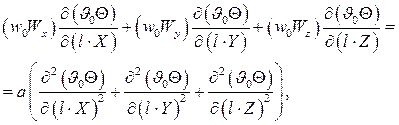
или: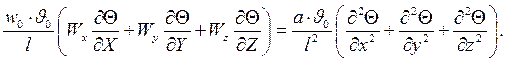

Поделив правую и левую части последнего уравнения на 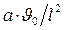, получим:

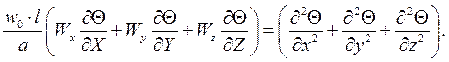(4.14)

В уравнении (4.14) появляется новый безразмерный комплекс

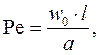
который носит название числа Пекле. Физический смысл числа Пекле в том, что оно характеризует соотношение интенсивностей переноса теплоты конвекцией и теплопроводностью в движущейся жидкости. Если Pe = 0, то имеет место только перенос теплоты теплопроводностью. Если Pe ® ¥, то переносом теплоты теплопроводностью можно пренебречь. Как правило, для движущихся капельных жидкостей (вода, воздух и т.д.) перенос теплоты конвекцией гораздо больше переноса теплоты теплопроводностью. Для движущихся жидких металлов (ртуть, жидкий натрий и т.д.) перенос теплоты конвекцией сравним с переносом теплоты теплопроводностью.

Число Пекле можно представить в виде:

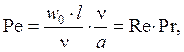
где Re = w₀l/n - число Рейнольдса; Pr - безразмерный критерий, называемый числом Прандтля, и определяемый выражением:

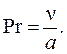
Число Прандтля Pr можно считать теплофизическим параметром жидкости, поскольку он равен отношению коэффициентов кинематической вязкости n и температуропроводности а. У капельных жидкостей число Прандтля, как и вязкость, значительно зависит от температуры (уменьшаясь с ростом температуры), и при обычных температурах Pr > 1. У газов число Прандтля слабо зависит от температуры, и по значению близко к единице (Pr » 1). У жидких металлов число Прандтля много меньше единицы (Pr << 1).

С учетом сделанных обозначений, уравнение (3.49) запишем в следующем виде:

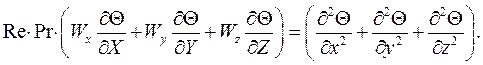(4.15)

Выражение (4.15) является уравнением энергии в безразмерном виде.

Уравнение теплоотдачи (4.12) запишем следующим образом:

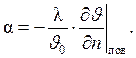
Подставляя в это выражение 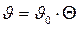, , 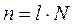получим:

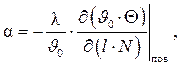или

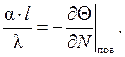(4.16)

В выражении (4.16) имеется новый безразмерный комплекс:

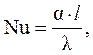
который носит название числа Нуссельта. По форме число Нуссельта Nu похоже на число Био Bi = a×l/l,однако, в числе Нуссельта l - это коэффициент теплопроводности жидкости, а в числе Био l - коэффициент теплопроводности твердого тела. Кроме того, число Био Bi в задачах теплопроводности является определяющим критерием, а число Нуссельта Nu в задачах конвективного теплообмена - определяемым критерием.

Уравнение теплоотдачи (4.12) в безразмерном виде имеет вид:

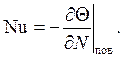(4.17)

Поскольку в безразмерное уравнение энергии (4.15) входят безразмерные компоненты скорости W_x, W_y, W_z, то для описания процесса конвективного теплообмена к уравнениям (4.15) и (4.17) нужно добавить безразмерные уравнения Навье-Стокса (3.19) или (3.20), и уравнение неразрывности (3.21).

Граничное условие для уравнения энергии (4.15) имеет вид:

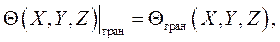(4.18)

где 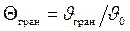- безразмерная температура на границах объема жидкости; X,Y,X – безразмерные координаты точек на границах. В частности, если температура поверхности тела t_п во всех точках постоянна, то на поверхности твердого тела выполняется условие:

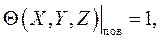
где X,Y,Z – безразмерные координаты точек на поверхности тела.

Если на входе рассматриваемую область жидкость имеет характерную температуру t₀, то безразмерная температура на входе равна нулю:

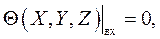
где X,Y,Z – безразмерные координаты точек на поверхности входа.

4.3 Уравнения подобия для процессов конвективного теплообмена

В системе уравнений конвективного теплообмена, включающей уравнения движения жидкости, определяющими критериями являются безразмерные координаты X, Y, Z; число Рейнольдса Re; число Грассгофа Gr (или число Галилея Ga); число Прандтля Pr (или число Пекле Pe). Определяемыми критериями являются безразмерная температура Q, и число Нуссельта Nu.

В результате решения системы уравнений конвективного теплообмена (4.15), (4.17), (4.18) и уравнений движения (3.19), (3.20), (3.21), (3.22) могут быть получены уравнения подобия, зависящие от вида движения жидкости.

При вынужденном движении жидкости уравнения подобия имеют следующий вид:

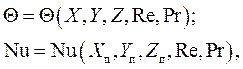(4.19)

где X_п, Y_п, Z_п - координаты поверхности тела, где происходит теплообмен.

При свободном движении жидкости уравнения подобия имеют такой вид:

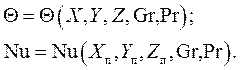(4.20)

При наличии вынужденного и свободного движения жидкости уравнения подобия имеют следующий вид:

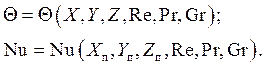(4.21)

Обычно интерес представляет температурное поле жидкости Q вблизи поверхности омываемого тела, т.к., зная его, по формуле (4.17) можно определить безразмерный коэффициент теплоотдачи - число Нуссельта Nu. По числу Нуссельта несложно определить размерный коэффициент теплоотдачи:

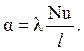
Отметим, что коэффициент теплоотдачи на поверхности твердого тела a, входящий в число Нуссельта Nu, экспериментально проще определить другими способами. Например, зная полный тепловой поток Q, Вт, подводимый изнутри к поверхности теплообмена площадью F, м², (например, при электрическом обогреве) рассчитывается средняя плотность теплового потока, подводимого к поверхности тела:

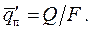
Если поверхность тела омывается капельной жидкостью, то средняя плотность теплового потока к жидкости за счет конвективного теплообмена 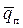равняется величине 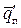: 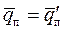. При омывании поверхности тела газом часть теплоты с поверхности уходит за счет излучения. В этом случае 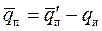, где q_и - плотность теплового потока за счет излучения:

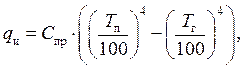
где С_пр – приведенный коэффициент излучения, Вт/(м²К⁴); Т_п, Т₀ – абсолютные температуры поверхности и газа, К.

После определения величины 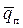определяется средний конвективный коэффициент теплоотдачи:

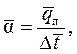
где 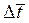- средний температурный напор между поверхностью твердого тела и жидкостью, понимаемый, как среднеинтегральный по поверхности тела.

Можно ввести среднее число Нуссельта:

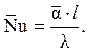
Число Нуссельта 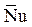, определенное по последнему выражению, не зависит от безразмерных координат поверхности X_п, Y_п, Z_п, и уравнения подобия для него в случае вынужденной и свободной конвекции имеют следующий вид:

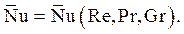(4.22)

При вынужденной конвекции в уравнении (4.22) исчезает число Грассгофа Gr, и уравнение подобия становится таким:

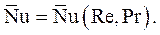(4.23)

При свободной конвекции в уравнении (4.22) исчезает число Рейнольдса Re, и уравнение подобия принимает вид:

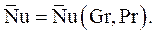(4.24)

В некоторых случаях при свободной конвекции применяют упрощенное уравнение подобия:

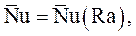
где Ra – безразмерный комплекс, называемый числом Рэлея, равный произведению чисел Грассгофа Gr и Прандтля Pr:

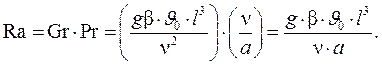
Если кроме одного характерного линейного размера l имеются другие характерные размеры омываемых твердого тела l₁, l₂ и т.д., то в уравнения подобия вводятся безразмерные симплексы (простые числа подобия): L₁ = l₁/l, L₂ = l₂/l, и т.д. Тогда, например, уравнения (4.21) будет иметь следующий вид:

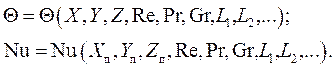(4.25)

При конвективном теплообмене (в отличие от простого движения жидкости) всегда происходит изменение температуры жидкости, как в направлении к поверхности тела, так и вдоль нее. Некоторые теплофизические параметры, входящие в числа подобия (например, n, l, а), значительно изменяются с температурой. Возникает вопрос, при какой температуре следует выбирать данные параметры. На данный вопрос нет однозначного ответа, и в качестве определяющей температуры, по которой выбирают теплофизические свойства, может выступать характерная температура жидкости t₀, температура поверхности тела t_п, их среднее (t₀+t_п)/2, среднемассовая температура жидкости t_ж и т.п. При физическом моделировании нужно следить, чтобы в модели и образце определяющая температура выбиралась одинаковым образом.

4.4 Физическое моделирование конвективного теплообмена

В п. 3.4 подробно рассмотрено физическое моделирование движения жидкости. Многое, изложенное там, относится и к моделированию конвективного теплообмена. Поскольку конвективный теплообмен в большой степени определяется движением жидкости, то в первую очередь нужно выполнить подобие процессов движения жидкости в образце и модели. Затем нужно обеспечить подобие температур на границах изучаемой области движения жидкости. Наконец, нужно осуществить равенство критериев подобия, характерных для процессов конвективного теплообмена (чисел Пекле Pe или Прандтля Pr). Перечислим кратко основные моменты физического моделирования конвективного теплообмена.

1) Необходимо осуществить геометрическое подобие образца и модели. Все размеры образца и модели, существенные для процесса движения жидкости, должны быть связаны между собой соотношением l = с_l×l¢, где l и l¢ - характерные линейные размеры образца и модели.

2) Необходимо обеспечить подобие физических условий для образца и модели. Теплофизические параметры (m, n, r, b, а) для образца и модели должны выбираться при определяющей температуре, которая выбирается одинаково для образца и модели. Однородные теплофизические параметры в образце и модели должны быть связаны соответствующим масштабом преобразования: j = c_j×j¢, где j и j¢ - физический параметр в образце и модели; c_j - константа подобия для данного физического параметра.

3) Необходимо выполнить подобие процессов на границах исследуемой жидкости в модели и в образце. Например, должно выполняться равенство безразмерных скоростей и температур на границах изучаемого объема:

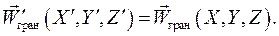
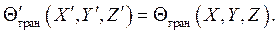
4) Необходимо обеспечить равенство определяющих одноименных критериев подобия в образце и модели, существенных для рассматриваемого процесса конвективного теплообмена. Тогда и определяемые безразмерные переменные в образце и модели также будут иметь одинаковые значения.

Допустим, изучается конвективный теплообмен при вынужденном движении жидкости. Уравнения подобия в этом случае описываются выражениями (4.19). Определяющими критериями подобия (кроме переменных координат X, Y, Z) являются число Рейнольдса Re и число Прандтля Pr. Для подобия процессов в модели и в образце требуется выполнение равенств:

Re¢ = Re,

Pr¢ = Pr.

При выполнении этих условий в сходственных координатах (X¢=X, Y¢=Y, Z¢=Z) будут равны безразмерные температуры и числа Нуссельта:

Q¢ = Q;

Nu¢ = Nu.

При свободном движении жидкости уравнения подобия при конвективном теплообмене имеют вид (4.20). Определяющими критериями подобия (кроме переменных координат X, Y, Z) являются число Грассгофа Gr и число Прандтля Pr. Для подобия процессов требуется выполнение равенств:

Gr¢ = Gr,

Pr¢ = Pr.

При выполнении этих условий в сходственных координатах будет равенство безразмерных температур Q и чисел Нуссельта (4.27), что в развернутом виде можно записать так:

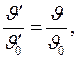или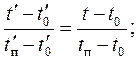

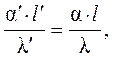
где величины со штрихом относятся к модели, без шриха – к образцу.

Из последних выражений можно выразить размерные величины в образце через размерные величины в модели:

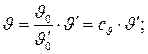
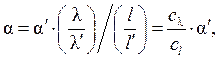
где 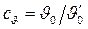; 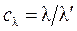- константы подобия по температуре и коэффициенту теплопроводности.

4.5 Получение эмпирических уравнений подобия

Обычно, опыты на модели проводят при различных определяющих параметрах (w₀, l₀, J₀, l, n, a и др.), принимающих ряд значений, как и соответствующие им определяемые параметры (J, a). Определяющие безразмерные критерии подобия (Re, Gr, Pr) при этом также принимают ряд значений, как и определяемые безразмерные числа подобия (Q, Nu).

Для начала нужно определить, каким уравнением подобия описывается данный случай конвективного теплообмена. Допустим, уравнение подобия имеет вид (4.23), характерный для теплообмена при вынужденной конвекции:

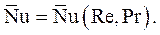
По данным измерений подсчитываются значения Re и Pr и соответствующие им значения 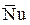. Зависимость между числами подобия обычно представляется в виде степенных функций, например:

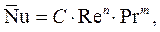(4.26)

где С, n, m являются постоянными безразмерными числами.

Зависимости типа (4.26) применимы лишь в тех пределах изменения аргумента, в которых подтверждены опытом.

Предположим, что число 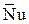зависит только от Re (или что опыты проводились с теплоносителем, число Прандтля которого является постоянной величиной). В этом случае

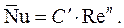
Логарифмируя последнее уравнение, получаем:

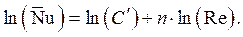
Обозначая 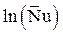через Y, 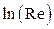через Х и 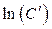через А, можно написать:

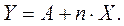
Последнее выражение является уравнением прямой линии. Показатель степени n представляет собой тангенс угла наклона прямой к оси абсцисс. Следовательно, значение n можно определить с помощью графического представления опытных данных в координатах 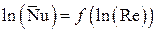(рис. 9).

Показатель степени n равен:

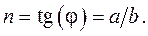
Постоянная С¢ определяется из уравнения

,

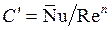которому удовлетворяет любая точка прямой.

Проверкой применимости степенной зависимости является то факт, что в логарифмических координатах все точки укладываются на прямую. Если же опытные точки располагаются по кривой, то эту кривую обычно заменяют ломаной. Для отдельных участков такой кривой значения С¢ и n различны.

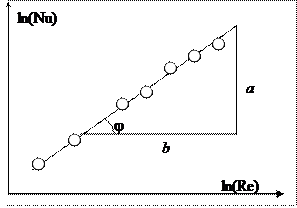
Рис. 9. К установлению зависимости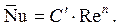

В случае, если искомая величина 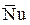является функцией двух аргументов, например, 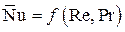, на графике появляется семейство прямых; второй аргумент берется в качестве параметра (рис. 10).

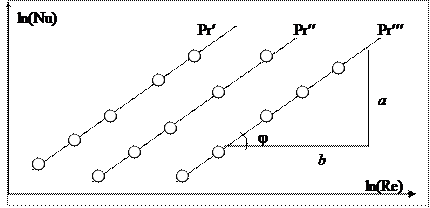
Рис. 10. К установлению зависимости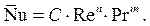

Тогда по одной из прямых определяют показатель n при числе Рейнольдса, а затем опытные данные представляют на графике в виде зависимости

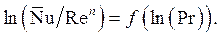
Из последнего графика определяют показатель m при критерии Прандтля, а затем по уравнению

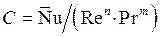
определяют значение коэффициента С.

Определяющий размер. В числа подобия входит характерный размер l. Теория подобия не определяет однозначно, какой размер должен быть принят за определяющий, т.е. тот размер, который будет принят как масштаб линейных размеров. Если в условиях однозначности заданы несколько размеров, за определяющий обычно принимают тот, который в большей степени отвечает физическому существу процесса. Остальные размеры входят в уравнение подобия в виде симплексов L₁ = l₁/l; L₂ = l₂/l и т.д.

Например, при течении жидкости в трубе диаметром d и длиной s в качестве характерного размера принимают l = d; симплексом является L₁ = s/d.

В некоторых случаях за определяющий линейный размер принимается комбинация разнородных физических величин, входящих в условия однозначности. Такая комбинация имеет размерность линейной величины.

Определяющая температура. В числа подобия входят физические параметры жидкости. При получении безразмерных переменных физические свойства часто считают постоянными. В действительности, поскольку температура жидкости переменна, изменяются и значения ее физических свойств. Поэтому при обработке данных по теплообмену важным является вопрос выбора так называемой определяющей температуры, по которой определяются значения физических параметров, входящих в числа подобия. За определяющую следует принимать такую температуру, которая в технических расчетах бывает задана или легко может быть вычислена.

При расчетах конвективного теплообмена по эмпирическим уравнениям подобия определяющие температуру и линейный размер необходимо выбирать точно так же, как это сделано при получении формулы. Неучет этого обстоятельства может привести к значительным ошибкам.

Вопросы для самоконтроля:

1) Напишите уравнение энергии без внутренних источников теплоты. Какой физический закон оно отражает?

2) Напишите выражение для полной производной температуры по времени. Чем эта производная отличается от частной производной температуры по времени?

3) При каком условии уравнение энергии совпадает с дифференциальным уравнением теплопроводности?

4) Напишите выражение, описывающее закон Фурье.

5) Напишите выражение для определения коэффициента теплоотдачи.

6) На основании какого условия выводится уравнение теплоотдачи, описывающее теплообмен между жидкостью и поверхностью тела?

7) Какие безразмерные числа подобия являются определяющими, а какие – определяемыми, в процессах конвективного теплообмена при вынужденной конвекции жидкости?

8) Напишите выражение для безразмерного числа Пекле и поясните его физический смысл.

9) Напишите выражение для безразмерного числа Нуссельта и объясните его физический смысл.

10) Что понимается под граничными условиями в процессах конвективного теплообмена?

11) Напишите уравнения подобия для конвективного теплообмена при вынужденном движении жидкости.

12) Сформулируйте условия моделирования процессов конвективного теплообмена при вынужденной и свободной конвекции жидкости.

13) В каком виде обычно представляют эмпирические уравнения подобия для расчета конвективного теплообмена?

14) Что такое определяющая температура, и каким образом она выбирается?

15) Что такое определяющий линейный размер тела, и как он выбирается?

Выводы по главе

В данном разделе приведены уравнения, описывающие конвективный теплообмен между поверхностью твердого тела и омывающей жидкостью, включающие в себя уравнение энергии, уравнение теплоотдачи, а также уравнения движения жидкости. Сформулированы условия однозначности для описания процессов конвективного теплообмена, включающие геометрические, физические и граничные условия. Получены уравнения конвективного теплообмена в безразмерном виде. Установлены определяющие и определяемые критерии подобия в процессах конвективного теплообмена при вынужденной и свободной конвекции жидкости. Установлены уравнения подобия для процессов конвективного теплообмена в общем и частных случаях. Рассмотрены условия моделирования процессов конвективного теплообмена при вынужденной и свободной конвекции. Рассмотрена методика получения эмпирических уравнений подобия для расчета процессов конвективного теплообмена.

Список литературы по теме

1. Исаченко В.П. Теплопередача: Учебник для вузов / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. – 4-е изд., перераб. и доп. – М.: Энергоиздат, 1981. – 416 с.

2. Кутателадзе С.С. Моделирование теплоэнергетического оборудования / С. С. Кутателадзе, В. А. Пермяков, Д. Н. Ляховский. – М.: Энергия 1966.

3. Мигай В.К. Моделирование теплообменного энергетического оборудования / В.К. Мигай. – Л.: Энергоатомиздат. Ленингр. Отд-ние, 1987. – 264 с.: ил.

4. Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Е.В. Аметистов, В.А. Григорьев, Б.Т. Емцев и др.; под общей редакцией В.А. Григорьева и В.М. Зорина. – М.: Энергоиздат, 1991. – 512 с., ил.

Заключение

В данном учебном пособии рассмотрены следующие разделы курса «Физическое моделирование процессов передачи теплоты»: основы теории подобия, физическое моделирование процесса теплопроводности, физическое моделирование движения жидкости, физическое моделирование конвективного теплообмена.

В первом разделе введены основные понятия теории подобия, рассмотрено применение теории подобия к потокам реальной жидкости, сформулированы основная теорема теории подобия и понятие автомодельности. Рассмотрены метод размеренностей и сформулировано основное правило моделирования.

Во втором разделе рассмотрено математическое описание процессов стационарной и нестационарной теплопроводности, уравнения подобия для процессов теплопроводности, охлаждение (нагревание) тела в условиях конвективного теплообмена и в условиях теплообмена излучением, моделирование процессов теплопроводности.

В третьем разделе приведены уравнения движения реальной жидкости, получено описание процесса движения жидкости в безразмерном виде, установлены уравнения подобия для процессов движения жидкости, рассмотрены условия моделирования процессов движения жидкости.

В четвертом главе приведены уравнения конвективного теплообмена. Получена система уравнений конвективного теплообмена в безразмерном виде. Установлены уравнения подобия для процессов конвективного теплообмена. Рассмотрены условия моделирования конвективного теплообмена. Рассмотрена методика получения эмпирических уравнений подобия.

В целом, учебное пособие содержит основной теоретический материал по дисциплине «Физическое моделирование процессов передачи теплоты», и может быть полезным для студентов, обучающихся по направлениям подготовки 13.03.01 – «Теплоэнергетика и теплотехника» (бакалавриат), 13.04.01 – «Теплоэнергетика и теплотехника» (магистратура).

Литература

1. Гухман А.А. Применение теории подобия к исследованию процессов тепло – массообмена / А.А. Гухман. – Изд. 2-е перераб. и доп. М., «Высшая школа», 1974. - 328 с.

2. Гухман А.А. Введение в теорию подобия / А.А. Гухман. – М.: Высшая школа, 1961. - 140 с.

3. Гухман А.А. Применение теории подобия к исследованию процессов тепло- и массообмена / А.А. Гухман. – М.: Высшая школа, 1967. - 86 с.

4. Исаченко В.П. Теплопередача: Учебник для вузов / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. – 4-е изд., перераб. и доп. – М.: Энергоиздат, 1981. – 416 с.

5. Кутателадзе С.С. Основы теории теплообмена. – Изд. 5-е перераб. и доп. – М.: Атомиздат, 1979. – 416 с.

6. Мигай В.К. Моделирование теплообменного энергетического оборудования / В.К. Мигай. – Л.: Энергоатомиздат. Ленингр. Отд-ние, 1987. – 264 с.: ил.

7. Михеев М.А. Основы теплопередачи / М.А. Михеев, И.М. Михеева. – Изд. 2-е, стереотип. М.: Энергия, 1977. – 344 с. С ил.

8. Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Е.В. Аметистов, В.А. Григорьев, Б.Т. Емцев и др.; под общей редакцией В.А. Григорьева и В.М. Зорина. – М.: Энергоиздат, 1991. – 512 с., ил.

Содержание

Предисловие……………………………………………………………3

Введение………………………………………………………………..4

1. Основы теории подобия………………………...............………...6

1.1 Основные понятия теории подобия………………………………6

1.2 Применение теории подобия к потокам

реальной жидкости………………………………………………..11

1.3 Основная теорема теории подобия………………………………18

1.4 Автомодельность………………………………………………….22

1.5 Метод размеренностей……………………………………………23

1.6 Основное правило моделирования……………………………….25

Вопросы для самоконтроля…………………………………………...28

Выводы по главе……………………………………………………….28

Список литературы по теме…………………………………………..29

2. Физическое моделирование процессов теплопроводности….30

2.1. Математическое описание процесса теплопроводности……….30

2.2. Описание процесса теплопроводности в безразмерном виде….32

2.3. Уравнения подобия для процесса теплопроводности…………..34

2.4. Охлаждение (нагревание) неограниченнойпластины…..……...36

2.5. Нагревание тела в условиях теплообмена излучением………...39

2.6. Процессы стационарной теплопроводности ……………………42

2.7. Моделирование процессов теплопроводности….........................44

Вопросы для самоконтроля…………………………………………...50

Выводы по главе……………………………………………………….51

Список литературы по теме…………………………………………..51

3. Физическое моделирование движения жидкости……………..52

3.1.Уравнения движения реальной жидкости……………………….52

3.2. Описание уравнений движения жидкости

в безразмерном виде………………………………………………57

3.3. Уравнения подобия для процессов движения жидкости……....60

3.4. Моделирование процессов движения жидкости………………..63

Вопросы для самоконтроля…………………………………………...69

Выводы по главе……………………………………………………….70