Определенный интеграл. Примеры решений

Для того, чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить соответствующие неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

Как видите, для того, чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому, если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще не совсем закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.

В общем виде определенный интеграл записывается так:

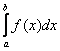
Что прибавилось по сравнению с неопределенным интегралом?

Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой a.

Верхний предел интегрирования стандартно обозначается буквой b.

Отрезок [a; b] включает граничные точки и называется отрезком интегрирования.

Что такое определенный интеграл? Можно посмотреть в учебниках про диаметр разбиения отрезка, предел интегральных сумм и т. д., но урок носит практический характер. Поэтому скажем, что определенный интеграл – это, прежде всего, самое что ни на есть обычное ЧИСЛО.

Есть ли у определенного интеграла геометрический смысл?Есть. И очень хороший. Самая популярная задача вычисления определённого интеграла – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл?Решить определенный интеграл – это значит, найти число, равное приращению первообразной функции на отрезке [a; b].

Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:

.

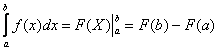Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию F(X) (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле никогда не добавляется.

Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись

?

Это подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: F(b).

3) Подставляем значение нижнего предела в первообразную функцию: F(a).

4) Рассчитываем (без ошибок!) разность F(b)-F(a), то есть, находим число, равное приращению первообразной (от подынтегральной) функции на отрезке [a; b].

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда существует всё, что мы напишем в виде определённого интеграла. Например, интеграла

не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример:

.

Такого интеграла тоже не существует на всём отрезке [-2; 3], так как в точках

,

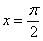
этого отрезка подынтегральная функция f(x) = tg(x) не существует.

Для того, чтобы определенный интеграл существовал на данном отрезке, необходимо, чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. Бывает так, что подолгу мучаешься с нахождением трудной первообразной, а когда наконец-то ее находишь, то ещё и ломаешь голову над вопросом: «что за ерунда получилась?». Например, если получилось примерно так:

???!!!

то нельзя подставлять отрицательные числа под корень! Если для решения в контрольной работе, на зачете или экзамене Вам предложен несуществующий интеграл вроде

,

то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике. Интеграл

преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

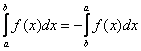
Например, в определенном интеграле перед интегрированием

целесообразно поменять пределы интегрирования на «привычный» порядок:

.

В таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

Это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям: .

Пример 1

Вычислить определенный интеграл

.

Решение:

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы

.

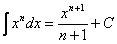(3) Используем формулу Ньютона-Лейбница

.

Сначала подставляем в x³ верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2

Вычислить определенный интеграл

.

Это пример для самостоятельно решения, решение и ответ в конце урока.

Пример 3

Вычислить определенный интеграл

.

Решение:

.

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.

СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряем на третьем слагаемом:

,

т. к. очень часто машинально пишут

.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, так:

.

Здесь устно использованы правила линейности, устно проинтегрированы табличные интегралы. Получилась всего одна скобка с отчёркиванием пределов:

(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию мы сначала подставили 4, затем –2, опять же выполнив все действия в уме.

При втором способе существует повышенный риск допустить ошибку в вычислениях, поэтому студенту-чайнику лучше использовать первый способ, чтобы не терять знаки.

Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная.

находится в одной скобке.