Для параболических уравнений
Рассмотрим смешанную задачу для уравнения с переменными коэффициентами:
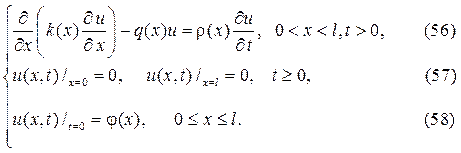
Предполагаем, что функции 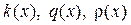 непрерывны на отрезке
непрерывны на отрезке
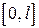 и выполнены неравенства
и выполнены неравенства
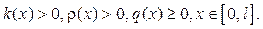
Будем искать решение задачи (56  58) в форме
58) в форме
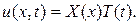 (59)
(59)
и подставляя (59) в (56), после разделения переменных получим
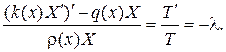 (60)
(60)
Из (57) и (59) вытекает, что функция Х(х) должна удовлетворять гранич- ным условиям 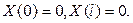 Присоединив эти граничные условия к дифференциальному уравнению для Х(х) получим, так называемую, зада- чу Штурма
Присоединив эти граничные условия к дифференциальному уравнению для Х(х) получим, так называемую, зада- чу Штурма  Лиувилля:
Лиувилля:
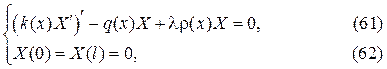
где нужно определить значения параметра 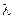 и соответствующие нетри-
и соответствующие нетри-
виальные решения Х(х).
Определение. Те значения параметра 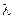 , для которых задача (61
, для которых задача (61  62) имеет нетривиальные решения, называются собственными значениями, а соответствующие нетривиальные решения называются собственными функциями.
62) имеет нетривиальные решения, называются собственными значениями, а соответствующие нетривиальные решения называются собственными функциями.
Ранее у нас встречалась задача Штурма  Лиувилля (37
Лиувилля (37  38) для урав-нения с постоянными коэффициентами и нахождение ее собственных функций базировалось на возможности найти явно общее решение диф- ференциального уравнения. Теперь мы имеем такую ситуацию, когда уравнение (61), вообще говоря, не интегрируется в квадратурах и в первую очередь возникает вопрос о существовании собственных значений и собственных функций и их свойствах.
38) для урав-нения с постоянными коэффициентами и нахождение ее собственных функций базировалось на возможности найти явно общее решение диф- ференциального уравнения. Теперь мы имеем такую ситуацию, когда уравнение (61), вообще говоря, не интегрируется в квадратурах и в первую очередь возникает вопрос о существовании собственных значений и собственных функций и их свойствах.
Справедливы следующие три теоремы.
Теорема 1. Задача Штурма  Лиувилля (61
Лиувилля (61  62) имеет счетное множес- тво положительных собственных значений
62) имеет счетное множес- тво положительных собственных значений
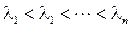
отвечающие различным собственным значениям, взаимно ортогональны друг другу с весом 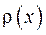 на отрезке
на отрезке 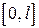 , т. е.
, т. е.
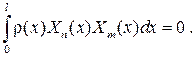
Теорема 3. Если f(x) имеет на 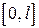 непрерывные производные до вто- рого порядка включительно и удовлетворяет граничным условиям
непрерывные производные до вто- рого порядка включительно и удовлетворяет граничным условиям
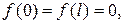 то она разлагается в абсолютно и равномерно сходящий- ся ряд Фурье по собственным функциям задачи (61
то она разлагается в абсолютно и равномерно сходящий- ся ряд Фурье по собственным функциям задачи (61  62)
62)
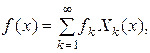
где коэффициенты Фурье вычисляются по формулам
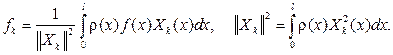
Считая задачу Штурма-Лиувилля решенной, вернемся к равенству (60) и решим дифференциальное уравнение
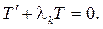
Очевидно, что 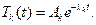 Теперь составляем ряд
Теперь составляем ряд
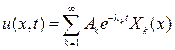 (63)
(63)
и определяем Аk так, чтобы выполнялось начальное условие (58), т. е.
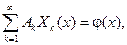
откуда в силу теорем 2 и 3 следует, что
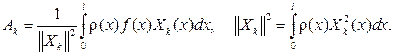 (64)
(64)
Итак найдено , что решение задачи (56  58) дается формулами (63), (64).
58) дается формулами (63), (64).
Заметим, что теорема 2 об ортогональности будет иметь место и для других задач Штурма  Лиувилля, если граничные условия (57) заменить на
Лиувилля, если граничные условия (57) заменить на 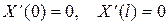 или, например,
или, например, 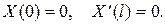 Более того, чуть позже рассмотрим так называемый особый случай, когда коэффи –циент k(х) обращается в нуль в точках х=0 и
Более того, чуть позже рассмотрим так называемый особый случай, когда коэффи –циент k(х) обращается в нуль в точках х=0 и 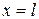 , и собственные функ- ции будут снова составлять ортогональную с весом ρ(х) систему функ- ций.
, и собственные функ- ции будут снова составлять ортогональную с весом ρ(х) систему функ- ций.
Разумеется, что рассмотренная задача Штурма  Лиувилля для уране-ния с переменными коэффициентами может возникнуть и при решении уравнений гиперболического или эллиптического типа. Если, например,
Лиувилля для уране-ния с переменными коэффициентами может возникнуть и при решении уравнений гиперболического или эллиптического типа. Если, например,
в правой части (56) заменить 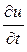 на
на 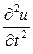 , то получим уравнение гипебо- лического типа с переменными коэффициентами, решение которого будет опираться на задачу (61
, то получим уравнение гипебо- лического типа с переменными коэффициентами, решение которого будет опираться на задачу (61  62).
62).
192. Имеется однородный тонкий стержень длиной 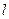 , изолированный от окружающего пространства, с начальной температурой
, изолированный от окружающего пространства, с начальной температурой 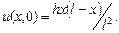 Определите температуру u(x,t) точек стержня при t>0, если концы стерж- ня поддерживаются при температуре, равной нулю.
Определите температуру u(x,t) точек стержня при t>0, если концы стерж- ня поддерживаются при температуре, равной нулю.
Р е ш е н и е. Поставленная задача равносильна смешанной задаче
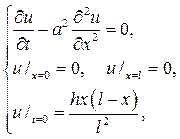
которую решаем методом Фурье, полагая 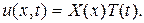 После подстановки в дифференциальное уравнение и разделения переменных найдем
После подстановки в дифференциальное уравнение и разделения переменных найдем
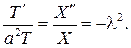
Из граничных условий получим
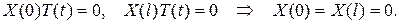
Теперь решаем задачу Штурма-Лиувилля:
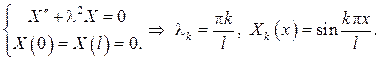
Из дифференциального уравнения 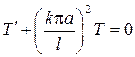 находим, что
находим, что
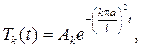
и, следовательно, решение смешанной задачи будет иметь вид
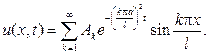
Определим коэффициенты Аk так, чтобы выполнялось начальное условие
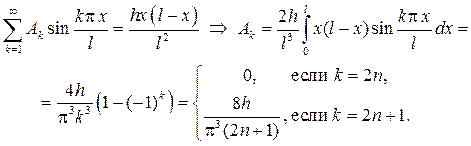
Подставляя значения коэффициентов в ряд, придем к ответу
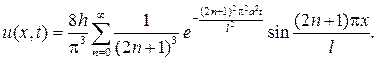
193. Растворенное вещество с начальной концентрацией u0 диффундиру- ет из раствора, заключенного между плоскостями х=0 и 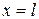 в раствори- тель ограниченный плоскостями x=h и
в раствори- тель ограниченный плоскостями x=h и 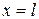 . Определить процесс вырав- нивания концентрации, предполагая, что границы х=0 и
. Определить процесс вырав- нивания концентрации, предполагая, что границы х=0 и 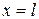 непроница- емы для вещества.
непроница- емы для вещества.
