Среднее квадратическое отклонение

.

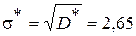6.5. По воздушной цели ведётся стрельба независимыми очередями, каждая из которых состоит из четырёх выстрелов. Случайная величина Х – число попаданий в цель для одной очереди. Произведено 30 очередей. Результаты опытов представлены в виде статистической совокупности:

xi
mi
pi*	0,1	0,2	0,4	0,2	0,1

Построить статистическую функцию распределения и определить статистическое математическое ожидание и статистическую дисперсию случайной величины Х.

Решение. Статистическая совокупность представляет собой статистическое распределение случайной величины Х. В приведённой таблице p_i^* означает относительную частоту события Х = x_i. Пользуясь данными статистической совокупности, можно приближенно построить статистическую функцию распределения F^*(x) (эмпирическую функцию распределения). Функция F^*(x) определяет для каждого значения х относительную частоту события Х < х. Заметим, что F^*(x) – неубывающая функция и

F^*(x) Î [0;1].

Если х₁ – наименьшая варианта, а х_k – наибольшая, то

F^*(x) = 0 при х £ х₁ и F^*(x) = 1 при х > х_k.

В данной задаче

F^*(0) = 0; F ^*(1) = 0,1;

F ^*(2) = 0,1 + 0,2 = 0,3;

F ^*(3) = 0,1 + 0,2 + 0,4 = 0,7;

F ^*(4) = 0,1 + 0,2 + 0,4 + 0,2 = 0,9;

F ^*(5) = 1.

График этой функции приведен на рис. 13

Статистическое математическое ожидание является точечной оценкой математического ожидания, которую можно найти по формуле

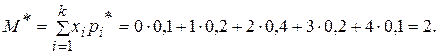
Несмещенная оценка дисперсии определяется по формуле

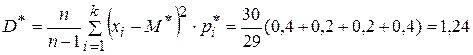
Рис. 13

Несмещенная оценка дисперсии определяется по формуле

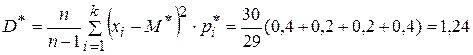
6.6. Произведено 400 бомбометаний с радиолокационным прицелом в приблизительно одинаковых условиях (высота 3000 м, скорость 900 км/ч). Случайная величина Х – отклонение бомбы по дальности от центра цели. Результаты опытов представлены в виде статистической совокупности:

xi (м)	-500 -400	-400 -300	-300 -200	-200 -100	-100
mi
pi*	0,01	0,03	0,07	0,14	0,25	0,24	0,15	0,08	0,02	0,01

Определить статистическое математическое ожидание M^* и статистическую дисперсию D^* случайной величины Х. Построить гистограмму данной статистической совокупности.

Решение. При непрерывном распределении признака весь интервал, в котором заключены все наблюдённые значения признака, разбивают на ряд частичных интервалов длины h и находят m_i – сумму частот вариантов, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длины h, а высоты равны отношению m_i / h (плотность частоты).

Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки. Искомая гистограмма частот изображена на рис. 14.

Рис. 14

Несмещенные оценки M ^* и D^* найдём, принимая середины интервалов в качестве вариантов:

M ^*= (-450)·0,01 + (-350) ·0,03 + (-250) ·0,07 + (-150) ·0,14 + (-50) ·0,25 + 50·0,24 +

+ 150·0,15 + 250·0,08 + 350·0,02 + 450·0,01 = 0.

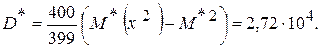
Оценка среднего квадратичного отклонения 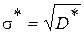характеризует рассеяние случайной величины Х:

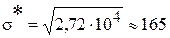м.

Оценка неизвестного параметра генеральной совокупности одним числом называется точечной оценкой.

Наряду с точечными оценками существует интервальное оценивание, когда по данным выборки строится числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри этого интервала находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом числе наблюдений, когда точечная оценка в значительной мере случайна, следовательно, мало надёжна.

6.7.Найти доверительный интервал для оценки с доверительной вероятностью 0,95 неизвестного математического ожидания a нормально распределённого признака Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение σ = 5, выборочная средняя a^* = 14 и объём выборки n = 25.

Решение. Для определения точности оценки a^* в математической статистике пользуются доверительными интервалами, а для определения надёжности – доверительными вероятностями. Доверительным называют интервал, который с заданной надёжностью β покрывает оцениваемый параметр.

Плотность вероятности нормально распределенной случайной величины имеет вид:

,

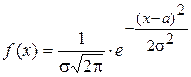где s - средне квадратичное отклонение, а – математическое ожидание.

Для оценки математического ожидания a нормально распределённой случайной величины Х по выборочной средней a^* при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал

,

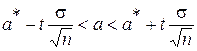где 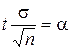; α - точность оценки; n – объём выборки; t – такое значение аргумента функции Лапласа (интеграла вероятностей)

,

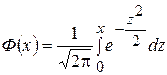при котором

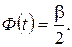
То есть

.

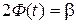Тогда вероятность

.

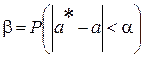Найдём доверительный интервал (a^*- α; a^* + α). Для этого найдем t. Из соотношения

2Ф(t) = 0,95

получим

Ф(t) = 0,475.

Функция Ф(х) протабулирована (табл. 2) и по этой таблице находим t = 1,96.

По данным

T = 1,96, a^* = 14, σ = 5, n = 25,

определим доверительный интервал

12,04 < a < 15,96.

6.8.Произведено 20 опытов над величиной Х. Результаты опытов приведены в таблице:

I	xi	I	xi	i	xi	i	xi
	10,9		10,4		10,8		10,6
	10,7		11,3		10,3		10,6
	11,0		10,8		10,5		10,8
	10,5		11,2		10,8		10,9
	10,6		10,9		10,9		10,7

Требуется найти оценку для математического ожидания а^* величины Х и построить доверительный интервал, соответствующий доверительной вероятности β = 0,9.

Решение. Здесь среднее квадратическое отклонение σ случайной величины Х не известно, поэтому в качестве ориентировочного значения дисперсии можно взять её точечную несмещённую оценку. По данным опытов найдем точечные оценки математического ожидания, дисперсии и среднего квадратического отклонения:

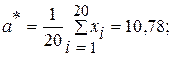
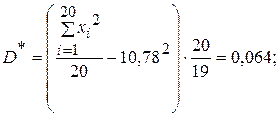
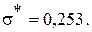
Доверительная вероятность 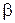, точность оценки 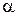и объем выборки n связаны между собой. Если определены две величины, то тем самым будет определена и третья.

Для выборки из нормальной генеральной совокупности доверительная вероятность 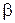для математического ожидания при неизвестном 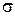определяется формулой

,

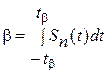где

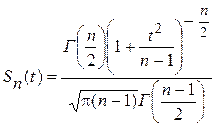
- закон распределения Стьюдента,

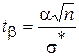
По заданной доверительной вероятности 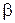и числу K = n - 1 можно найти значения 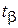из табл. 3 (приложение).

.

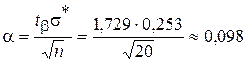В нашем случае K = 19, 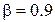, поэтому ,

.

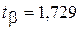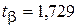откуда

.

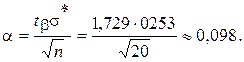Искомые границы доверительного интервала для матаматического ожидания будут:

верхняя: 10,78 + 0,098 = 10,878;

нижняя: 10,78 + 0,098 = 10,682.

Таким образом, доверительный интервал, соответствующий доверительной вероятности β = 0,9 меет вид

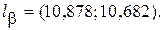
6.9.Выборка из большой партии электроламп содержит сто ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 часов. Найти с надёжностью 0,95 доверительный интервал для средней продолжительности а горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы σ = 40 часов.

Решение. Здесь n = 100, а^* = 1000, b = 0,95, σ = 40. Поэтому

T = Ф^-1(0,95/2)=1,96.

Точность оценки α вычислим по формуле

,

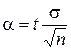то есть

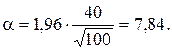
Затем найдем доверительные границы:

a* - α = 1000 - 7,84 = 992,16

a* + α = 1000 + 7,84 = 1007,84

и доверительный интервал

l_b= (992,16; 1007,84).

6.10.Произведено пять независимых равноточных измерений для определения заряда электрона. Опыты дали следующие результаты (в абсолютных электростатических единицах):

4,781 · 10^-10 , 4,795· 10^-10 ,

4,769 · 10^-10 , 4,792 · 10^-10 ,

4,779· 10^-10.

Определить оценку величины заряда электрона и найти доверительные границы при доверительной вероятности 99 %, считая, что ошибки нормальны и измерения не имеют систематических ошибок.

Решение. Оценкой величины заряда электрона является среднее арифметическое полученных результатов измерений:

.

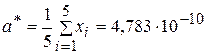Для неизвестного среднего квадратического отклонения найдем несмещенную оценку

,

.

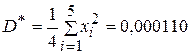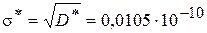Для нахождения доверительных границ

,

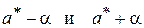определим величину t_β по табл. 3 (приложение) при β = 0,99 и n – 1 = 4. Эта величина равна t_β = 4,60, поэтому

.

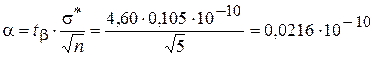Таким образом, искомые границы доверительного интервала для величины заряда электрона будут:

верхняя 4,783·10^-10 + 0,0216·10^-10 = 4,8046·10^-10

нижняя 4,783·10^-10 - 0,0216·10^-10 = 4,7614·10^-10

Это означает, что интервал

l_β = ( 4,7614·10^-10; 4,8046·10^-10),

с доверительной вероятностью 99 % накрывает оцениваемый параметр.