Математическое ожидание

Математическим ожиданием случайной величины X называется среднее значение .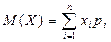

1. M(C) = C

2. M(CX) = CM(X), где C = const

3. M(X ± Y) = M(X) ± M(Y)

4. Если случайные величины X и Y независимы, то M(XY) = M(X)·M(Y)

Дисперсия

Дисперсией случайной величины X называется

D(X) = S(x – M(X))²p = M(X²) – M²(X).

Дисперсия представляет собой мерой отклонения значений случайной величины от своего среднего значения.

1. D(C) = 0

2. D(X + C) = D(X)

3. D(СX) = C²D(X), где C = const

4. Для независимых случайных величин

D(X ± Y) = D(X) + D(Y)

5. D(X ± Y) = D(X) + D(Y) ± 2Cov(x, y)

Квадратный корень из дисперсии случайной величины X называется средним квадратичным отклонением .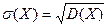

@ Задача 3: Пусть случайная величина X принимает всего два значения (0 или 1) с вероятностями q, p, где p + q = 1. Найти математическое ожидание и дисперсию.

Решение:

M(X) = 1·p + 0·q = p; D(X) = (1 – p) ²p + (0 – p) ²q = pq.

@ Задача 4: Математическое ожидание и дисперсия случайной величины X равны 8. Найти математическое ожидание и дисперсия случайных величин: а) X – 4; б) 3X – 4.

Решение: M(X – 4) = M(X) – 4 = 8 – 4 = 4; D(X – 4) = D(X) = 8; M(3X – 4) = 3M(X) – 4 = 20; D(3X – 4) = 9D(X) = 72.

@ Задача 5: Совокупность семей имеет следующее распределение по числу детей:

xi	x1	x2
pi	0,1	p2	0,4	0,35

Определить x₁, x₂ и p₂, если известно, что M(X) = 2; D(X) = 0,9.

Решение: Вероятность p₂ равна p₂ = 1 – 0,1 – 0,4 – 0,35 = 0,15. Неизвестные x находятся из уравнений: M(X) = x₁·0,1 + x₂·0,15 + 2·0,4 + 3·0,35 = 2; D(X) = 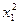·0,1 + 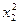·0,15 + 4·0,4 + 9·0,35 – 4 = 0,9. x₁ = 0; x₂ = 1.

Генеральная совокупность и выборка. Оценки параметров

Выборочное наблюдение

Статистическое наблюдение можно организовать сплошное и не сплошное. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности (генеральной совокупности). Генеральная совокупность это множество физических или юридических лиц, которую исследователь изучает согласно своей задачи. Это часто экономически невыгодно, а иногда и невозможно. В связи с этим изучается только часть генеральной совокупности – выборочная совокупность.

Результаты, полученные на основе выборочной совокупности, можно распространить на генеральную совокупность, если следовать следующим принципам:

1. Выборочная совокупность должна определяться случайным образом.

2. Число единиц выборочной совокупности должно быть достаточным.

3. Должна обеспечиваться репрезентативность (представительность) выборки. Репрезентативная выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать.

Типы выборок

В практике применяются следующие типы выборок:

а) собственно-случайная, б) механическая, в) типическая, г) серийная, д) комбинированная.

Собственно-случайная выборка

При собственно-случайной выборке отбор единиц выборочной совокупности производится случайным образом, например, посредством жеребьевки или генератора случайных чисел.

Выборки бывают повторные и бесповторные. При повторной выборке единица, попавшая в выборку, возвращается и сохраняет равную возможность снова попасть в выборку. При бесповторной выборке единица совокупности, попавшая в выборку, в дальнейшем в выборке не участвует.

Ошибкиприсущие выборочному наблюдению, возникающие в силу того, что выборочная совокупность не полностью воспроизводит генеральную совокупность, называются стандартными ошибками. Они представляют собой среднее квадратичное расхождение между значениями показателей, полученных по выборке, и соответствующими значениями показателей генеральной совокупности.

Расчетные формулы стандартной ошибки при случайном повторном отборе следующая: 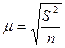, а при случайном бесповторном отборе следующая: 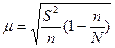, где S² – дисперсия выборочной совокупности, n/N – доля выборки, n, N - количества единиц в выборочной и генеральной совокупности. При n = N стандартная ошибка m = 0.

Механическая выборка

При механической выборке генеральная совокупность разбивается на равные интервалы и из каждого интервала случайным образом отбирается по одной единице.

Например, при 2%-ной доли выборки из списка генеральной совокупности отбирается каждая 50-я единица.

Стандартная ошибка механической выборки определяется как ошибка собственно-случайной бесповторной выборки.

Типическая выборка

При типической выборке генеральная совокупность разбивается на однородные типические группы, затем из каждой группы случайным образом производится отбор единиц.

Типической выборкой пользуются в случае неоднородной генеральной совокупности. Типическая выборка дает более точные результаты, потому что обеспечивается репрезентативность.

Например, учителя, как генеральная совокупность, разбиваются на группы по следующим признакам: пол, стаж, квалификация, образование, городские и сельские школы и т.д.

Стандартные ошибки типической выборки определяются как ошибки собственно-случайной выборки, с той лишь разницей, что S² заменяется средней величиной от внутригрупповых дисперсий.

Серийная выборка

При серийной выборке генеральная совокупность разбивается на отдельные группы (серии), затем случайным образом выбранные группы подвергаются сплошному наблюдению.

Стандартные ошибки серийной выборки определяются как ошибки собственно-случайной выборки, с той лишь разницей, что S² заменяется средней величиной от межгрупповых дисперсий.

Комбинированная выборка

Комбинированная выборка является комбинацией двух или более типов выборок.

Точечная оценка

Конечной целью выборочного наблюдения является нахождение характеристик генеральной совокупности. Так как этого невозможно сделать непосредственно, то на генеральную совокупность распространяют характеристики выборочной совокупности.

Принципиальная возможность определения средней арифметической генеральной совокупности по данным средней выборки доказывается теоремой Чебышева. При неограниченном увеличении n вероятность того, что отличие выборочной средней 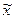от генеральной средней 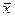будет сколь угодно мало, стремится к 1.

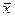
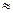
Это означает, что характеристика генеральной совокупности 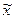с точностью 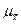. Такая оценка называется точечной.

Интервальная оценка

Базисом интервальной оценки является центральная предельная теорема.

Интервальная оценка позволяет ответить на вопрос: внутри какого интервала и с какой вероятностью находится неизвестное, искомое значение параметра генеральной совокупности?

Обычно говорят о доверительной вероятности p = 1 – a, с которой 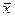будет находиться в интервале 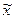– D < 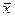< 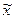+ D, где D = t_крm > 0 предельная ошибка выборки, a - уровень значимости (вероятность того, что неравенство будет неверным), t_кр - критическое значение, которое зависит от значений n и a. При малой выборке n < 30 t_кр задается с помощью критического значения t-распределения Стъюдента для двустороннего критиерия с n – 1 степенями свободы с уровнем значимости a (t_кр(n – 1, a) находится из таблицы «Критические значения t–распределения Стъюдента», приложение 2). При n > 30, t_кр - это квантиль нормального закона распределения (t_кр находится из таблицы значений функции Лапласа F(t) = (1 – a)/2 как аргумент). При p = 0,954 критическое значение t_кр = 2 при p = 0,997 критическое значение t_кр = 3. Это означает, что предельная ошибка обычно больше стандартной ошибки в 2-3 раза.

Таким образом, суть метода выборки заключается в том, что на основании статистических данных некоторой малой части генеральной совокупности удается найти интервал, в котором с доверительной вероятностью p находится искомая характеристика генеральной совокупности (средняя численность рабочих, средний балл, средняя урожайность, среднее квадратичное отклонение и т.д.).

@ Задача 1.Для определения скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 22 дням ( 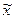= 22) со стандартным отклонением 6 дней (S = 6). С вероятностью p = 0,954 определить предельнуюошибку выборочной средней и доверительный интервал средней продолжительности расчетов предприятий данной корпорации.

Решение: Предельнаяошибка выборочной средней согласно (1) равна D = 2·0,6 = 1,2, а доверительный интервал определяется как (22 – 1,2; 22 + 1,2), т.е. (20,8; 23,2).

§6.5 Корреляция и регрессия