Предел функций в точке: определение, геометрический смысл. Односторонние пределы. Основные теоремы о пределах функций. Замечательный предел
1 замечательный предел. 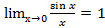
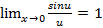 при u
при u 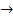 o при x
o при x 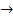 o
o
Справедливы формулы:
1) 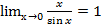 3)
3) 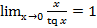
2) 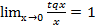 4)
4) 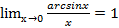
При помощи 1 замечательного предела раскрывается неопределенность 
Пример:
1) 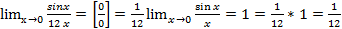
Замечательный предел
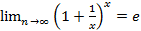 e
e 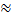 2,7182
2,7182
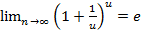 , где
, где 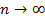 при
при 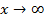
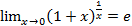 ,
,
Справедливы формулы
1) 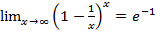 3)
3) 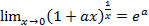
2) 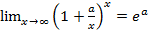
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Число 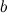 называется правым пределом функции
называется правым пределом функции 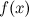 в точке
в точке  , если для
, если для 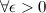
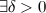 такое, что для любого
такое, что для любого 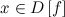 и
и 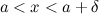 , выполняется неравенство
, выполняется неравенство 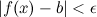 (рис. 1). Правый предел обозначается
(рис. 1). Правый предел обозначается 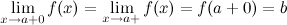
Число 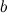 называется левым пределом функции
называется левым пределом функции 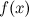 в точке
в точке  , если для
, если для 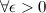
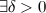 такое, что для любого
такое, что для любого 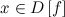 и
и 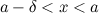 , выполняется неравенство
, выполняется неравенство 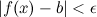 (рис. 2). Левый предел обозначается
(рис. 2). Левый предел обозначается 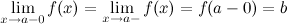
Геометрический смысл.
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции 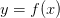 в точке
в точке 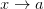 существует и равен
существует и равен 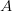 , если для любой
, если для любой  -окрестности точки
-окрестности точки 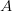 можно указать такую
можно указать такую 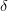 -окрестность точки
-окрестность точки  , что для любого
, что для любого  из этой
из этой 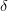 -окрестности значение
-окрестности значение 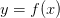 будет находится в
будет находится в  -окрестности точки
-окрестности точки 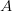 .
.
Отметим, что по определению предела функции в точке для существования предела при 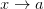 не важно, какое значение принимает функция в самой точке
не важно, какое значение принимает функция в самой точке  . Можно привести примеры, когда функция не определена при
. Можно привести примеры, когда функция не определена при  или принимает значение, отличное от
или принимает значение, отличное от 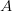 . Тем не менее, предел может быть равен
. Тем не менее, предел может быть равен 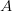 .
.
Теоремы о пределах
1. Бесконечно большие и бесконечно малые.
Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < dимеет место неравенство |f(x)| > M.
limx® a=¥
2. Функция ограниченная при x® a.
3. Функция ограниченная при x® ¥.
4. Теорема. Если limx® a f(x)=b, то функция f(x) ограниченная при x® a.
5. Бесконечно малые и их свойства. limx® a a(x)=0
Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® af(x)=b, то можно записать f(x)=b+a(x).
Теорема. 2. Если limx® a a(x)=0 и a(x) ¹ 0, то 1/a® ¥.
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
6. Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) £ z(x) £ v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах").
7. Первый замечательный предел.

при n® ¥ имеет предел, заключенный между 2 и 3.
25.Понятие предела функции на бесконечности. Бесконечно малые и бесконечно большие функции, их свойства. Замечательный предел.
Определение: функция y=f(x)-называется бесконечно малой если

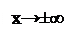 Lim f(x)=0 или lim f(x)=0
Lim f(x)=0 или lim f(x)=0
Определение: функция y=f(x)- называется бесконечно большой если:
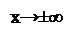
 Lim f(x)=∞ или lim f(x)=∞
Lim f(x)=∞ или lim f(x)=∞
1)Если f(x)- бесконечно малой, то 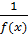 – бесконечно большой
– бесконечно большой
Lim f(x)=0, то lim 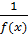 =
= 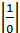 =∞
=∞
2) Если f(x)- бесконечно большой, то 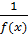 – бесконечно малой
– бесконечно малой
Lim f(x)=∞, то lim 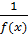 =
= 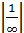 =0
=0
Свойства пределов
Пусть lim f(x) и lim g(x) – существуют
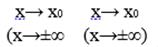
1)lim (f(x)±g(x))=lim f(x)+lim g(x)
2)lim (f(x)·g(x))=lim f(x)·lim g(x)
3)lim 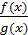 =
= 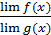 (lim g(x)≠0)
(lim g(x)≠0)
4) lim c=c (c-число)
