Студент должен иметь навыки
· Нахождения неопределенных интегралов
· Решения дифференциальных уравнений первого порядка и сводящиеся к ним
· Решения линейных однородных дифференциальных уравнений с постоянными коэффициентами
3. Структура дисциплины
| Семестр 1 | Трудоемкость в кредитных ед. | Часы Общ/ауд | Контрольные мероприятия | Рейтинг Макс/мин |
| Модуль1 Интегральное исчисление функций одной переменной | 63/45 | КР, ДЗ, РК | 35/22 | |
| Модуль 2 Дифференциальные уравнения | 60/40 | КР, ДЗ, РК | 35/22 | |
| Модуль 3 Итоговый контроль | Экзамен | 30/16 |
Содержание дисциплины
Виды учебной работы
| Виды учебной работы | Объем в часах по семестрам | |
| Всего | 02 семестр 17 недель | |
| Лекции | ||
| Семинары | ||
| Лабораторные работы | ||
| Практические занятия | ||
| Самостоятельная работа | ||
| Итого в часах | ||
| Итого в зачетных единицах: | ||
| Проверка знаний: | экзамен |
Модуль 1. Интегральное исчисление функций одной переменной
1. Неопределенные интегралы. Первообразная, её свойства. Неопределенный интеграл, его свойства, связь с дифференциалом. Таблица основных неопределенных интегралов. Интегрирование подстановкой и заменой переменного. Интегрирование по частям. Рациональные дроби. Разложение правильной рациональной дроби на сумму. Интегрирование простейших дробей. Интегрирование правильных и неправильных рациональных дробей.
2. Определенные интегралы. Задачи, приводящие к неопределенному интегралу. Определенный интеграл как предел интегральных сумм. Теорема об интегрируемости кусочно-непрерывных функций. Геометрическая интерпретация определенного интеграла. Основные свойства определенного интеграла. Теоремы об оценке и о среднем значении. Определенный интеграл с переменным верхним пределом и теорема о его производной. Формула Ньютона-Лейбница. Вычисление определенных интегралов подстановкой и по частям.
3. Несобственные интегралы. Несобственные интегралы по бесконечному промежутку (1-го рода). Несобственные интегралы от неограниченных функций на отрезке (2-го рода). Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Несобственные интегралы с несколькими особенностями.
4. Приложения определенных интегралов. Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрически и в полярных координатах. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. Вычисление длины дуги кривой и площади поверхности вращения
Модуль 2. Дифференциальные уравнения.
5. Дифференциальные уравнения первого и высших порядков.ДУ первого порядка, его решения. Частные и общие решения. Интегральные кривые. Задача Коши для ДУ 1-го порядка. Теорема Коши о существовании и единственности решения ДУ Геометрический смысл ДУ 1-го порядка. Метод изоклин. Дифференциальные уравнения n-го порядка, частные и общие решения. Задача Коши и ее геометрическая интерпретация (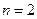 
). Теорема Коши о существовании и единственности решения ДУ (без док-ва). Краевая задача. Понижение порядка некоторых типов ДУ n-го порядка
6. Линейные дифференциальные уравнения.Линейные дифференциальные уравнения (ЛДУ) n-го порядка, однородные и неоднородные. Теорема о существовании и единственности решения. Дифференциальный оператор L[y], его свойства. Линейное пространство решений однородного ЛДУ (ОЛДУ). Линейно зависимые и независимые системы функций на отрезке. Определитель Вронского (вронскиан). Теорема о вронскиане системы линейно зависимых функций. Теорема о вронскиане системы линейно зависимых решений ОЛДУ. Теорема о структуре общего решения ОЛДУ. Размерность пространства решений ОЛДУ. Фундаментальная система решений ОЛДУ. Формула Остроградского-Лиувилля и ее следствия. Однородные ЛДУ с постоянными коэффициентами. Характеристическое уравнениеОЛДУ.Построение общего решения по корням характеристического уравнения. Неоднородные линейные ДУ (НЛДУ). Структура общего решения НЛДУ. Теорема о наложении частных решений. Метод Лагранжа вариации постоянных.
7. Системы дифференциальных уравнений.Нормальные системы ДУ. Задача и теорема Коши. Частные и общее решения. Системы линейных ДУ первого порядка. Определитель Вронского. Фундаментальная система решений. Однородные системы ЛДУ с постоянными коэффициентами. Характеристическое уравнение системы. Построение общего решения по корням характеристического уравнения (вывод только для случая действительных и различных корней). Теорема о структуре общего решения неоднородной системы ЛДУ. Метод вариации постоянных.