Системы многомерного управления. Общие сведения
В случае синтеза оптимального цифрового П-регулятора задача синтеза имеет вид: дан объект управления 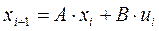 ;
; 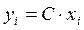 , требуется задать настроечные положительно определенные матрицы регулятора Q,R и наблюдателя Q1,R1 (например, единичные), и найдя параметры регулятора K, наблюдателя L и компенсатора Kz
, требуется задать настроечные положительно определенные матрицы регулятора Q,R и наблюдателя Q1,R1 (например, единичные), и найдя параметры регулятора K, наблюдателя L и компенсатора Kz
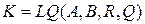 ,
, 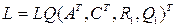 ,
, 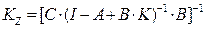 ,
,
где функция 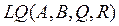 определена в виде
определена в виде
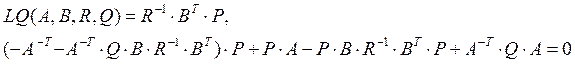
записать модель цифрового регулятора в виде
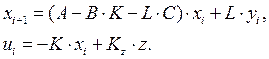
Если в результате моделирования переходной процесс получился неудовлетворительным, следует изменить настроечные матрицы и процедуру повторить снова.
Программа реализации регулятора имеет вид:
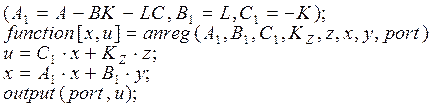
Возможен вариант синтеза модального цифрового П регулятора (чаще всего апериодического), когда матрица К выбирается из условия 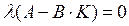 , а матрица L из условия
, а матрица L из условия 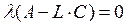 . Возможен и комбинированный вариант, например, когда синтезируется оптимальный регулятор и апериодический наблюдатель или наоборот.
. Возможен и комбинированный вариант, например, когда синтезируется оптимальный регулятор и апериодический наблюдатель или наоборот.
В случае синтеза оптимального цифрового ПИ-регулятора для объекта управления 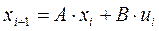 ;
; 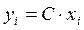 , требуется определить расширенные матрицы в виде
, требуется определить расширенные матрицы в виде
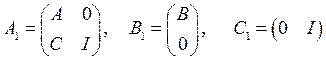
задать настроечные положительно определенные матрицы регулятора Q,R и наблюдателя Q1,R1 (например, единичные), и найдя параметры регулятора K инаблюдателя L
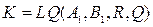 ,
, 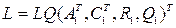 ,
,
записать модель цифрового регулятора в виде
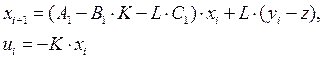
Синтез оптимального цифрового П-регулятора для одномерного типового объекта
Дан объект вида 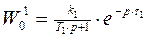 или
или 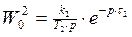 . Переведя модель в дискретное время, запишем
. Переведя модель в дискретное время, запишем
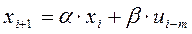 ,
,
где 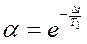 ;
; 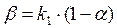 для системы, эквивалентной
для системы, эквивалентной 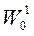 ;
;
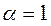 ;
; 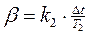 для системы, эквивалентной
для системы, эквивалентной 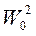 .
.
С учетом запаздывания матрицы системы 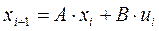 ;
; 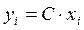 имеют вид
имеют вид
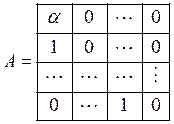
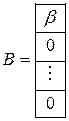
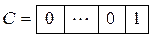
Приняв весовые матрицы Q, R в виде
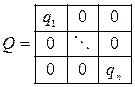 ;
; 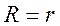
получим, что 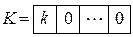 , где
, где 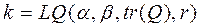 ,
, 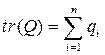 .
.
Матрицу апериодического наблюдателя 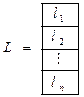 для использования в регуляторе можно найти в виде
для использования в регуляторе можно найти в виде 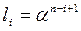 , где
, где 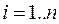 .
.
Синтез системы управления для простейшего многомерного объекта
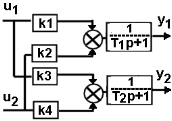 Пусть модель объекта имеет вид
Пусть модель объекта имеет вид
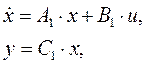
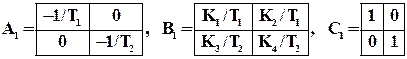
Переведем систему в дискретное время:
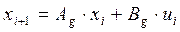 ;
; 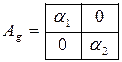 ;
; 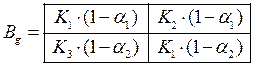 ;
; 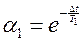 ;
; 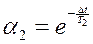 .
.
Для упрощения решения выберем теперь весовую матрицу
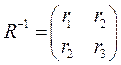
таким образом, чтобы произведение 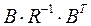 стало диагональной матрицей. Тогда, выбрав
стало диагональной матрицей. Тогда, выбрав 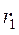 и
и 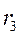 , найдем
, найдем
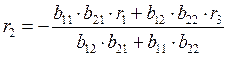 ,
, 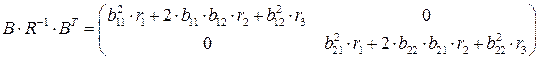 .
.
Теперь, поскольку все матрицы, входящие в уравнение Риккати в LQ(.), диагональны, матрица Р тоже диагональна и нахождение ее диагональных элементов сводится к решению двух независимых квадратных уравнений. Решение существует, если уравнения содержат положительные корни. Настройка качества переходных процессов производится выбором диагональной матрицы Q.
Синтез апериодического регулятора
Для простейшего многомерного объекта, модель которого описана в п.6., производится по условию 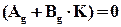 , откуда регулятор получается в виде
, откуда регулятор получается в виде 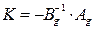 ,
, 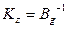 .
.
Программа реализации регулятора имеет вид