Задача для самостоятельного решения

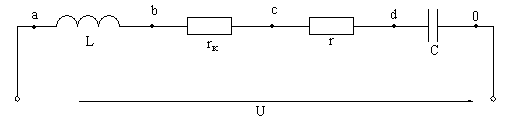
Для неразветвленной цепи определить ток, активную (Р), реактивную (Q) и полную (S) мощности, напряжения на всех элементах, а также построить векторную диаграмму. Частота тока f = 50Гц. При какой величине емкости С наступит резонанс напряжений.

U = 220 B; L = 0,05 Гн; r_к = 70 Ом; r = 13 Ом; С = 190 мкФ.

Лабораторная работа №4

Исследование разветвленной электрической
цепи синусоидального тока.

Цель работы

Подтвердить основные теоретические соотношения для однофазной цепи синусоидального тока при параллельном соединении реальной индуктивной катушки и конденсаторов экспериментом. В частности, подтвердить законы Ома и Кирхгофа для цепей синусоидального тока, явление резонанса токов и основные энергетические соотношения.

Теоретическая часть.

Действующее значение тока в каждой из параллельных ветвей определяется по закону Ома для синусоидального тока

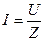, (4.1)

где U – действующее значение напряжения, приложенное к группе параллельно соединенных приемников;

Z – модуль комплексного сопротивления соответствующей ветви.

Если параллельная ветвь содержит несколько последовательно соединенных приемников, то модуль комплексного сопротивления этой ветви равен

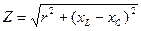, (4.2)

где r – активное сопротивление;

x_L, x_C – соответственно индуктивное и емкостное резисторные сопротивления.

Ток в каждой параллельной ветви состоит из активной – I_a и реактивной – I_p составляющих, определяемых по формулам:

I_a = Icosφ; (4.3)

I_p = Isinφ. (4.4)

где φ – угол сдвига фаз.

Ток в неразветвленной части цепи при параллельном соединении приемников определяется из выражения

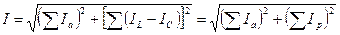(4.5)

где 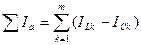– сумма активных составляющих токов в отдельных ветвях;

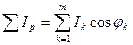– алгебраическая сумма реактивных составляющих токов в отдельных ветвях цепи;

I_L, I_C – соответственно индуктивный и емкостный реактивные токи.

При известных I, U и Р каждой ветви из формул

P = Scosφ; (4.6)

S = UI. (4.7)

Определяется угол сдвига фаз в неразветвленной части цепи

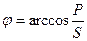. (4.8)

В лабораторной работе I, U и Р определяются по показаниям соответствующих приборов.

Реактивная мощность цепи определяется по формуле

Q = UIsinφ. (4.9)

Кроме того реактивную мощность цепи можно определить как алгебраическую сумму реактивных мощностей ветвей:

.

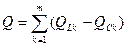При резонансе токов ΣI_L = ΣI_C, следовательно, ток в неразветвленной части цепи I = ΣI_a будет меньше, чем при любом другом режиме работы цепи. Режим параллельного контура, при котором сдвиг фаз между напряжением и током равен нулю, называется резонансом токов.

Для более глубокого анализа электрического состояния цепей синусоидального тока применяются векторные диаграммы. Построение векторных диаграмм начинают с выбора масштаба тока и напряжения. Масштабы тока и напряжения выбираются независимыми друг от друга.

Построение векторной диаграммы на комплексной плоскости начинают с построения в масштабе напряжения комплекса приложенного к цепи напряжения, полагая, что начальная фаза его равна нулю. Поэтому комплекс приложенного к цепи напряжения направляется по действительной оси. Под углом φ_с относительно комплекса приложенного напряжения направляется комплекс тока конденсатора в масштабе тока, а под углом φ_к комплекс тока индуктивной катушки, также в масштабе тока.

Угол φ_к определяется по формуле

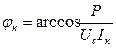, (4.10)

где U_c – напряжение сети;

Iк – ток катушки.

При исследовании электрического состояния разветвленной электрической цепи наиболее характерны случаи, когда b_L > b_C, b_L = b_C (условие возникновения резонанса токов), b_L < b_C (здесь b_L – реактивная индуктивная проводимость, b_C – реактивная емкостная проводимость). Для указанных случаев на рис.1.1 построены векторные диаграммы напряжения и токов.

Реактивные проводимости:

– емкостная

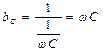; (4.11)

– индуктивная

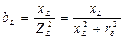, (4.12)

С – емкость конденсатора.

В лабораторной работе емкость конденсатора рассчитывается из формулы

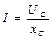(4.13)

определяется емкостное сопротивление конденсатора.

Затем из формулы

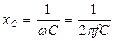, (4.14)

где f – частота сети

определяется емкость конденсатора.

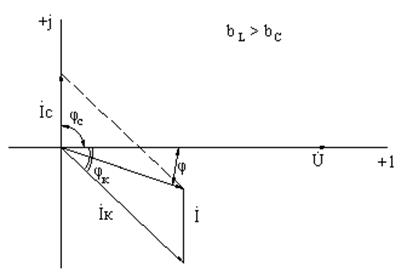
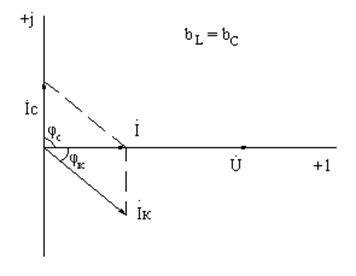
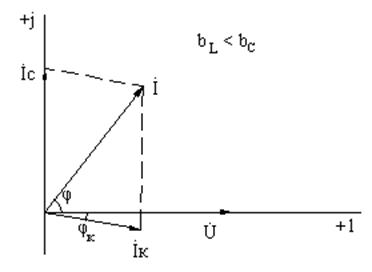
Рис.4.1. Векторные диаграммы