Понятие о внутренней и внешней задаче
Перенос тепла
Законы переноса тепла.
1. Молекулярный перенос тепла
q = 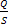
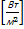 = - λgrad t - закон Фурье , кондуктивный перенос тепла, λ – коэффициент (пропорциональности) теплопроводности. Температурное поле – скалярное. Производная от температуры в направлении ее наиболее интенсивного изменения – grad t – векторная величина.
= - λgrad t - закон Фурье , кондуктивный перенос тепла, λ – коэффициент (пропорциональности) теплопроводности. Температурное поле – скалярное. Производная от температуры в направлении ее наиболее интенсивного изменения – grad t – векторная величина.
2. q= α 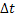 - конвективный перенос тепла. α – коэффициент теплоотдачи. Закон Ньютона – Рихмана.
- конвективный перенос тепла. α – коэффициент теплоотдачи. Закон Ньютона – Рихмана.
3. Перенос лучистого потока тепла – закон Стефана – Больцмана.
q=C0T4 , Со- константа излучения абсолютно черного тела (коэффициент пропорциональности).
Тепловые балансы в теплообменной аппаратуре
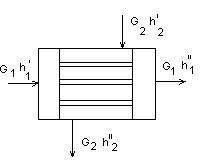 h = ct – теплосодержание потока, не меняющего агрегатное состояние.
h = ct – теплосодержание потока, не меняющего агрегатное состояние.
h = ct + r, теплосодержание потока, меняющего агрегатное состояние, где r – скрытая теплота превращения (испарения).
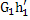 +
+ 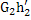 =
= 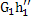 +
+ 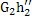
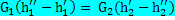
· Оба потока не меняют агрегатного состояния
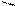
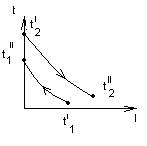
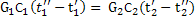 , разница температур (t2-t1)– локальная движущая сила движущая сила потока
, разница температур (t2-t1)– локальная движущая сила движущая сила потока
· Один поток меняет, другой не меняет агрегатное состояние
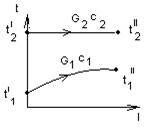
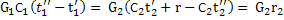
· Оба потока меняют агрегатное состояние
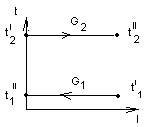
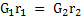
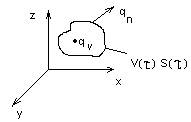
Вывод основного уравнения переноса тепла
Выводится из закона сохранения тепловой энергии. Изменение количества тепла в подвижном объеме 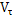 равно главному вектору теплового потока через поверхность, ограничивающую объем и результату действия объемных источников (стоков) тепла в объеме
равно главному вектору теплового потока через поверхность, ограничивающую объем и результату действия объемных источников (стоков) тепла в объеме 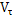 .
.
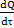 =
= 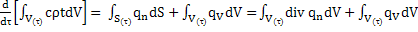
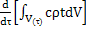 =
= 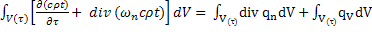
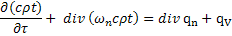
Среда изотропная - получаем уравнение Фурье – Кирхгофа:
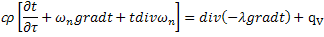
c =const,  ; div ωn=0- уравнение неразрывности; qn=-λ grad t- кондуктивный перенос тепла.
; div ωn=0- уравнение неразрывности; qn=-λ grad t- кондуктивный перенос тепла.
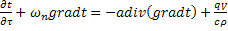 ; λ=const.
; λ=const.
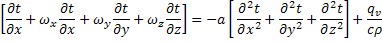
a = 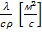 – коэффициент температуропроводности (коэффициент переноса теплоты),
– коэффициент температуропроводности (коэффициент переноса теплоты), 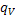 - удельный источник (сток) теплоты.
- удельный источник (сток) теплоты.
Граничные условия:
Условия сопряжения температурных полей и тепловых потоков на границе раздела сред.
t(o, 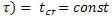 - I рода
- I рода
q (o, 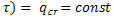 - II рода
- II рода
λ 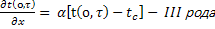
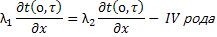
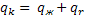 ,
, 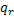 = 1
= 1 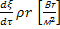
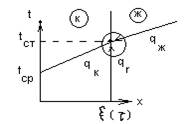
λк 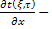 λж
λж 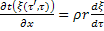 – условие Стефана
– условие Стефана
Теория теплового подобия
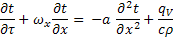
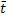 =
= 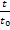 – безразмерная температура,
– безразмерная температура, 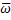 =
= 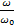 ,
, 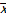 =
= 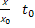 ,
, 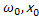 - характерные значения параметров
- характерные значения параметров
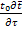 +
+ 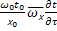 = -
= - 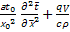
Нормируем уравнение по комплексу множителей при члене уравнения, характеризующем кондуктивный перенос тепла:
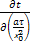 +
+ 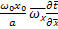 = -
= - 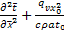
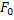 =
= 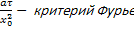 ; Pe =
; Pe = 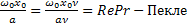 , где
, где 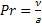 - критерий Прандтля (отношение коэффициента переноса механической и тепловой энергии)
- критерий Прандтля (отношение коэффициента переноса механической и тепловой энергии)
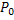 =
= 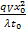 - физический смысл критериев теплового подобия – соотношение интенсивностей соответствующего механизма переноса тепла к кондуктивному теплопереносу.
- физический смысл критериев теплового подобия – соотношение интенсивностей соответствующего механизма переноса тепла к кондуктивному теплопереносу.
Понятие о внутренней и внешней задаче
Обезразмеривая граничное условие III рода, получаем:
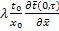 =
= 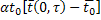


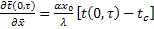 Bi =
Bi = 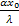 - соотношение конвективного переноса тепла в окружающей среде к кондуктивному теплопереносу в рассматриваемой области.
- соотношение конвективного переноса тепла в окружающей среде к кондуктивному теплопереносу в рассматриваемой области.



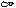

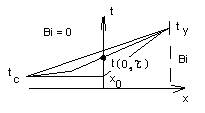
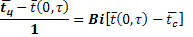
Bi 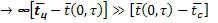 - внутренняя задача переноса тепла;
- внутренняя задача переноса тепла;
Bi => 0 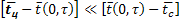 - внешняя задача переноса тепла.
- внешняя задача переноса тепла.
Условие Стефана:
λ 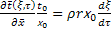
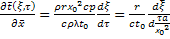 =
= 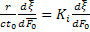
Ki = 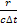 – отношении скрытого тепла к аккумулированному – критерий Кирпичева
– отношении скрытого тепла к аккумулированному – критерий Кирпичева
Pe 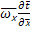 =
= 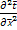


 Pe => 0, Re=> 0,
Pe => 0, Re=> 0, 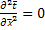 ,
, 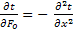 – уравнения стационарного и нестационарного кондуктивного переноса тепла.
– уравнения стационарного и нестационарного кондуктивного переноса тепла.
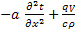 = 0 – уравнение стационарного кондуктивного переноса тепла с распределенными объемными источниками тепла.
= 0 – уравнение стационарного кондуктивного переноса тепла с распределенными объемными источниками тепла.
Pe => 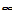 ; Re =>
; Re => 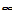
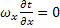 , но
, но 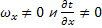 т.е. имеем дело с так называемым тепловым парадоксом, который можно разрешить лишь в приближении пограничного слоя.
т.е. имеем дело с так называемым тепловым парадоксом, который можно разрешить лишь в приближении пограничного слоя.
