Свойства определенного интеграла
Будем предполагать в дальнейшем, что a < b.
1. 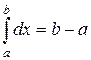 . Это свойство следует непосредственно из определения: f(x)=1,
. Это свойство следует непосредственно из определения: f(x)=1, 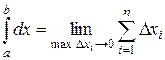 =
= 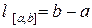 .
.
2. 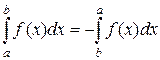 . Это утверждение также следует из определения интеграла
. Это утверждение также следует из определения интеграла 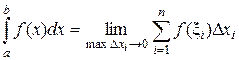 . Так как предел не зависит от выбора точек
. Так как предел не зависит от выбора точек 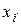 разбиения промежутка и от выбора промежуточных точек
разбиения промежутка и от выбора промежуточных точек 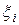 , то в интегральных суммах для
, то в интегральных суммах для 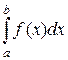 и для
и для 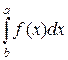 можно взять одни и те же точки деления х1, х2 , ..., хп и xi одни и те же. Тогда интегральные суммы будут отличаться только знаком , т.к. для первой интегральной суммы Dхi = xi – xi–1> 0, а для второй Dхi = xi–1 – xi < 0, откуда и следует свойство. Это свойство позволяет распространить понятие определенного интеграла на случай, когда отрезок [a, b] пробегается от a к b.
можно взять одни и те же точки деления х1, х2 , ..., хп и xi одни и те же. Тогда интегральные суммы будут отличаться только знаком , т.к. для первой интегральной суммы Dхi = xi – xi–1> 0, а для второй Dхi = xi–1 – xi < 0, откуда и следует свойство. Это свойство позволяет распространить понятие определенного интеграла на случай, когда отрезок [a, b] пробегается от a к b.
3. 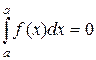 . Для доказательства этого свойства можно использовать предыдущее. Действительно, из свойства
. Для доказательства этого свойства можно использовать предыдущее. Действительно, из свойства 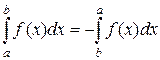 следует
следует 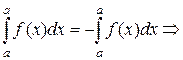
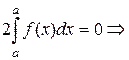
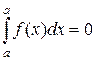 .
.
Это свойство позволяет распространить понятие определенного интеграла на отрезок нулевой длины.
4. Каково бы не было расположение точек a, b, c , имеет место равенство 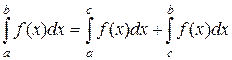 . Действительно, точку с можно рассматривать как точку разбиения отрезка [a , b].
. Действительно, точку с можно рассматривать как точку разбиения отрезка [a , b].
 |
Тогда интегральная сумма разобьется на две – по отрезку [a , с] и по отрезку [с , b], а так как предел суммы функций равен сумме пределов, то получится указанное свойство. Если же с не лежит на отрезке [a , b], а, например, с > b , то рассмотрим интеграл по промежутку [a , с] и к нему применим только что доказанное свойство: 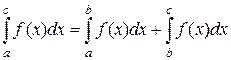 , откуда получим
, откуда получим 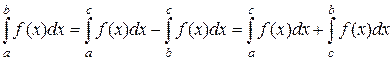 . ЧТД.
. ЧТД.
5. 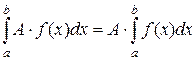 .
.
6. 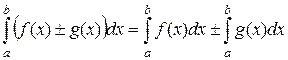 . Эти два свойства непосредственно следуют из определения определенного интеграла и свойств пределов.
. Эти два свойства непосредственно следуют из определения определенного интеграла и свойств пределов.
7. Если g(x) £ f(x) на [a, b] , то 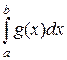 £
£ 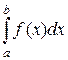 .
.
В частности , если f(x) ³ 0 на [a, b] , то 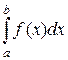 ³ 0;
³ 0;
если же f(x) > 0, то и 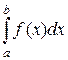 > 0.
> 0.
Аналогично, для f(x) £ 0 имеем 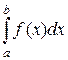 £ 0,
£ 0,
а если f(x) < 0, то и 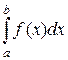 < 0.
< 0.
Эти свойства также следуют из определения определенного интеграла и теоремы о предельном переходе в неравенстве.
Заметим, что это свойство позволяет обобщить геометрическую интерпретацию определенного интеграла  и на случай f(x) £ 0. Действительно, если f(x) £ 0, то g(x) = – f(x) ³ 0 на [a, b] , графики этих функций симметричны относительно оси ОХ, а значит, криволинейные трапеции, ограниченные этими кривыми, равновелики. (рис 2), т.е. S1 = S2
и на случай f(x) £ 0. Действительно, если f(x) £ 0, то g(x) = – f(x) ³ 0 на [a, b] , графики этих функций симметричны относительно оси ОХ, а значит, криволинейные трапеции, ограниченные этими кривыми, равновелики. (рис 2), т.е. S1 = S2
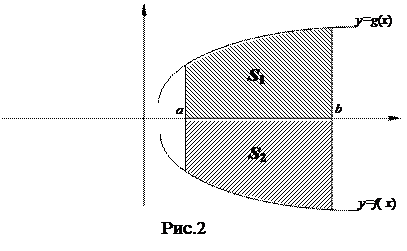
Поэтому, по свойству 4, S2 = S1 = 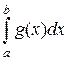 = –
= – 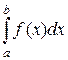 . Т.е. площадь криволинейной трапеции, расположенной под осью ОХ, равна соответствующему интегралу, взятому со знаком минус.
. Т.е. площадь криволинейной трапеции, расположенной под осью ОХ, равна соответствующему интегралу, взятому со знаком минус.
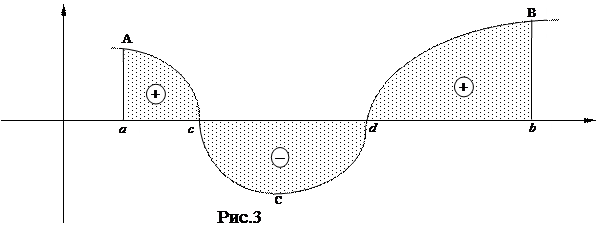
Учитывая также свойство 3, можно сформулировать следующее правило: если функция f(x) на отрезке [a, b] принимает значения разных знаков, то площадь фигуры, ограниченной графиком этой функции и осью ОХ на этом отрезке численно равна алгебраической сумме интегралов от этой функции по частичным отрезкам, на каждом из которых функция сохраняет знак, причем областям, расположенным под осью ОХ, соответствуют интегралы, взятые в этой сумме со знаком минус (рис.3):
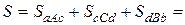
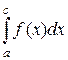 –
– 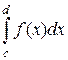 +
+ 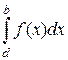
 |
8. Если на [a, b] т £ f(x) £ М, то т(a–b) £ 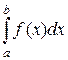 £М(a–b). Это свойство легко доказывается применение свойств 7 и 1.
£М(a–b). Это свойство легко доказывается применение свойств 7 и 1.
9. 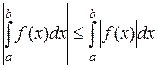 . Это свойство следует из неравенства
. Это свойство следует из неравенства 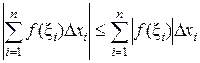 .
.
10. Теорема о среднем . Если функция f(x) непрерывна, а функция g(x) интегрируема и знакопостоянна на [a, b], то $ по крайней мере одна точка сÎ[a, b] такая , что имеет место равенство
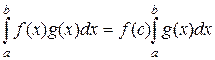
Для доказательства обозначим буквами т и М – наименьшее и наибольшее значения функции f(x) на отрезке [a, b] и для определенности будем считать, что g(x) ³ 0. Тогда последовательно находим
т £ f(x) £ М,
т g(x) £ f(x)g(x) £ М g(x),
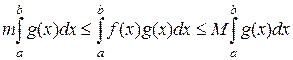 .
.
Предположим, что функция g(x) не равна тождественно нулю. Тогда по свойству 7 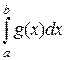 > 0 и
> 0 и 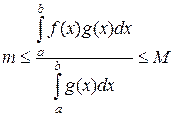 . Так как функция f(x) непрерывна на [a, b], то по теореме Больцано-Коши она принимает все промежуточные между т и М значения. Значит, существует хотя бы одна точка сÎ[a, b] такая, что
. Так как функция f(x) непрерывна на [a, b], то по теореме Больцано-Коши она принимает все промежуточные между т и М значения. Значит, существует хотя бы одна точка сÎ[a, b] такая, что
f(с) = 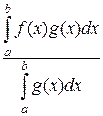 , откуда получим
, откуда получим 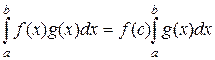 .
.
Если же функция g(x) = 0 тождественно на [a, b], то теорема, очевидно, справедлива: 0 = f(с).0 " сÎ[a, b].
 Если g(x) = 1 , то получим частный вид теоремы о среднем
Если g(x) = 1 , то получим частный вид теоремы о среднем

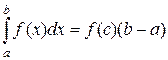 или f(с) =
или f(с) = 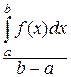
Эти равенства называются формулами среднего значения, а величина f(с) называется средним значением функции f(х) на отрезке [a, b].
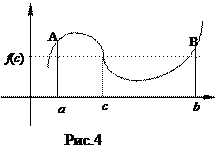
формула среднего значения имеет простой геометрический смысл: существует такое число х = с из [a, b], что площадь прямоугольника со сторонами f(с) и (b – а) равна площади криволинейной трапеции аАВb (рис.4)