Многокритериальные задачи оптимизации

Методы принятия компромиссных решений широко применяются в практике оптимизации многокритериальных задач.

Рассмотрим сначала общие положения в решении таких задач. Сначала опреде­ляются критерии оптимизации в порядке их важности: W_t, W₂, .... W_n.

Будем считать, что каждый из них нужно обратить в минимум или максимум. Сначала найдем решения, обращающие в минимум (максимум) главный критерий оптимизации W_t.

В практике чаще приходится иметь дело не с одним, а с несколькими критерия­ми оптимизации, что существенным образом усложняет выбор оптимального решения. Такого рода многокритериальные задачи составляют предмет векторной оптимизации. Одним из подходов в решении таких задач является метод Порето [18]. Покажем это на примере.

Пусть имеются критерии оптимизации W, и W₂ , которые, например, желательно максимизировать. Заметим, что весьма просто перейти от максимума к минимуму. В результате эксперимента получены десять решений: х₁, х₂.......х₃, каждому решению соответствуют определенные значения W_t и W₂ (рис. 2.4). Очевидно, что из всего множества решений эффективными будут лишь решения х₁, х₄ и x₇.

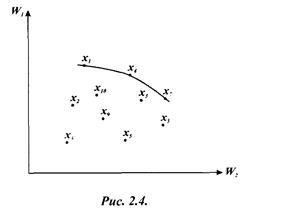
Принцип Порето не определяет единственное решение, он только сужает число альтернатив.

Различают три основных подхода в принятии компромисса.

Аддитивные критерии предусматривают образование целевой функции путем сложения нормированных значений частных критериев. При этом следует оперировать не с «натуральными», а с нормированными частными критериями, представляющими собой отношение «натурального» частного критерия к некоторой норми­рованной величине, измеряемой в тех же единицах, что и сам критерий. Выбор величины нормированного показателя может быть обоснован в следующих двух подходах.

Первый подход предполагает принимать в качестве нормированного критерия некоторое значение, директивно заданное заказчиком. Слабым моментом является негласное предположение того, что такое заданное нормированное значение являет­ся оптимальным.

Второй подход предполагает принимать в качестве нормированного делителя некоторое максимальное значение, достигнутое в области принимаемых решений. Возможен еще один подход, когда в качестве нормированного делителя принимается разность между максимальным и минимальным значениями критерия в области компромисса.

Целевая функция оптимизации имеет вид:

,

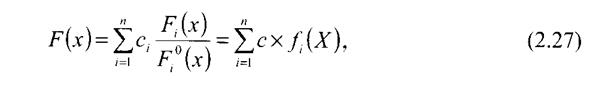
где: с_i -весовой коэффициент г-го частного критерия;

F_i°(x) -i-ый нормирующий делитель;

F_i(X) - нормированное значение i-го частного критерия.

Функция (2.27)позволяет осуществлять компромисс, когда улучшение одного критерия компенсирует ухудшение значений других. Весовые коэффициенты учитывают различную значимость частных критериев. Определение весовых коэффициентов осуществляется на основании методов экспертных оценок и других формальных процедур и носит субъективный характер.

Другим недостатком аддитивных критериев является взаимная компенсация частных критериев. Например, значительное уменьшение одного из критериев вплоть до нуля может быть перекрыто возрастанием других. Ослабить этот недостаток можно, если ввести ограничения на минимальные значения частных критериев и их весовые коэффициенты.

Таким образом, функция (2.27) осуществляет компромисс, при котором ухудшение одних нормированных частных критериев компенсируется улучшением других. Составление аддитивных критериев выступает как формальный математический прием, обеспечивающий задаче удобный для решения вид.

Если аддитивные критерии основаны на использовании принципа справедливой компенсации абсолютных значений нормированных частных критериев, то мультип­ликативные критерии оперируют не с абсолютными, а с относительными измене­ниями значений частных критериев.

Что же следует считать справедливым компромиссом.

Справедливым следует считать такой компромисс, когда суммарный уровень относительного снижения значения одного или ряда критериев не превышает суммарного уровня относительного увеличения значений других критериев.

Математическая формула условия оптимальности на принципе справедливой компенсации имеет вид:

где: ΔF, (х) - приращение i-го критерия;

F_i (х) - первоначальное значение i-го критерия.

Считая ΔF, (x)< F_i(х), представим (2.28) в виде дифференциала натурального логарифма:

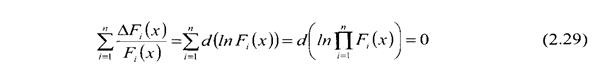
Анализ выражения (2.29) позволяет сформулировать обобщенный мультипликативный критерий оптимальности:

Мультипликативный критерий образуется путем простого перемножения частных критериев.

В случае, когда параметры имеют различную важность, в них вводятся весовые коэффициенты с,:

Существенным недостатком данных критериев является субъективность в назначении численных значений весовых коэффициентов. Здесь следует руководствоваться опытом предыдущих исследований и др.

Мультипликативные критерии не требуют нормирования, но имеют недостаток, заключающийся в том, что они компенсируют недостаточную величину одного частного критерия избыточной величиной другого, сглаживают неравнозначные их первоначальные значения.

При рассмотрении сложных объектов и наличии большого числа частных критериев довольно трудно, а иногда и невозможно установить аналитическую взаимосвязь между ними.

Принцип максимильных критериев оптимизации основан на идее равномерного компромисса, когда стараются найти такие значения переменных Х=(х₁....х_n), при которых нормированные значения всех частных критериев становятся равными между собой:

Введение весовых коэффициентов важности трансформирует выражение (2.32) в соотношение:

Принцип максимина заключается в такой вариации переменных X, при которых последовательно повышаются нормированные параметры, численные значения которых в начальном положении оказались наименьшими. Это неизбежно приводит к снижению значений части остальных критериев.

При определенной повторяемости таких операций происходит выравнивание противоречивых частных критериев. Таким образом, принцип максимина формулируется следующим образом: необходимо выбрать некоторое значение Х⁰ Х, на котором реализуются максимум из минимальных значений частных критериев. Принцип выбора X⁰ иногда называют принципом гарантированного результата, заимствованным из теории игр [18].

При минимизации частных критериев f,(x) самым «слабым» критерием является тот, который принимает максимальное значение. Формулировка принципа равномерной компенсации имеет вид:

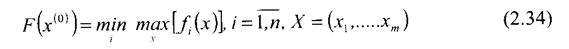
Принцип минимакса может интерпретироваться геометрически, когда каждый вариант объекта с п частными критериями представлен в пространстве Е_n в виде точки А¹, а множество вариантов может быть отображено в конечном множестве точек А, заключенных в выпуклую оболочку. Область принятия решений при этом ограничена выпуклой оболочкой S(A) в пространстве Еⁿ.