Постановка задачи оптимизации
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
- количество продукции - расход сырья";
- количество продукции - качество продукции".
Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого.
Типичный пример неправильной постановки задачи оптимизации: "Получить максимальную производительность при минимальной себестоимости". Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая:
а) получить максимальную производительность при заданной себестоимости;
б) получить минимальную себестоимость при заданной производительности.
В первом случае критерий оптимизации – производительность, а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод). Оптимизируемый вариант объекта или его работы должен оцениваться какой-то количественной мерой -критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность). Однако в частных задачах оптимизации, когда объект является частью технической системы или технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить техническая или технологическая характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход продукта, степень превращения, температура). Но в любом случае любой критерий оптимальности имеет экономическую природу.
Критерий оптимальности должен иметь ясный физический смысл, отражать наиболее существенные стороны системы или процесса, должен иметь количественную оценку.
В том случае, когда случайные возмущения невелики и их воздействие на объект можно не учитывать, критерий оптимальности может быть представлен как функция входных, выходных и управляющих параметров: R=R(X1, X2,...,XN, Y1,Y2,...,YN, U1,U2,..., UN).
Так как Y=f(U), то при фиксированных Х можно записать: R=R(U1,U2,..., UN).
При этом всякое изменение значений управляющих параметров двояко сказывается на величине R:
- прямо, так как управляющие параметры непосредственно входят в выражение критерия оптимизации;
- косвенно, через изменение выходных параметров системы или процесса, которые зависят от управляющих.
Как правило, для конкретных задач оптимизации технических систем критерий оптимальности не может быть записан в виде аналитического выражения.
В принципе, для оптимизации вместо математической модели можно использовать и сам объект, однако оптимизация опытным путем имеет ряд существенных недостатков:
а) необходим реальный объект;
б) необходимо изменять параметры технической системы в значительных пределах, что не всегда возможно;
в) длительность испытаний и сложность обработки данных.
Наличие математической модели (при условии, что она достаточно надежно описывает систему) позволяет значительно проще решить задачу оптимизации аналитическим либо численным методами.
Итак, для решения задачи оптимизации необходимо:
а) составить математическую модель объекта оптимизации;
б) выбрать критерий оптимальности и составить целевую функцию;
в) установить возможные ограничения, которые должны накладываться на переменные;
г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.
Методы оптимизации
При решении конкретной задачи оптимизации исследователь прежде всего должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой задачи оптимизации, а также используемой математической моделью объекта оптимизации.
В настоящее время для решения оптимальных задач применяют в основном следующие методы:
- методы исследования функций классического анализа;
- методы, основанные на использовании неопределенных множителей Лагранжа;
- вариационное исчисление;
- динамическое программирование;
- принцип максимума;
- линейное программирование;
- нелинейное программирование.
В последнее время разработан и успешно применяется для решения определенного класса задач метод геометрического программирования.
Как правило, нельзя рекомендовать какой-либо один метод, который можно использовать для решения всех без исключения задач, возникающих на практике. Одни методы в этом отношении являются более общими, другие - менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, методы нелинейного программирования) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием или принципом максимума.
Отметим также, что некоторые методы специально разработаны или наилучшим образом подходят для решения оптимальных задач с математическими моделями определенного вида. Так, математический аппарат линейного программирования, специально создан для решения задач с линейными критериями оптимальности и линейными ограничениями на переменные и позволяет решать большинство задач, сформулированных в такой постановке. Так же и геометрическое программирование предназначено для решения оптимальных задач, в которых критерий оптимальности и ограничения представляются специального вида функциями позиномами.
Динамическое программирование хорошо приспособлено для решения задач оптимизации многостадийных процессов, особенно тех, в которых состояние каждой стадии характеризуется относительно небольшим числом переменных состояния. Однако при наличии значительного числа этих переменных, т. е. при высокой размерности каждой стадии, применение метода динамического программирования затруднительно вследствие ограниченных быстродействия и объема памяти вычислительных машин.
Пожалуй, наилучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различных методов оптимизации. Ниже дана краткая характеристика наиболее распространненых методов и областей их применения, что до некоторой степени может облегчить выбор того или иного метода для решения конкретной оптимальной задачи.
Методы исследования функций классического анализа представляют собой наиболее известные методы решения несложных оптимальных задач, с которыми известны из курса математического анализа. Обычной областью использования данных методов являются задачи с известным аналитическим выражением критерия оптимальности, что позволяет найти не очень сложное, также аналитическое выражение для производных. Полученные приравниванием нулю производных уравнения, определяющие экстремальные решения оптимальной задачи, крайне редко удается решить аналитическим путем, поэтому, как, правило, применяют вычислительные машины. При этом надо решить систему конечных уравнений, чаще всего нелинейных, для чего приходится использовать численные методы, аналогичные методам нелинейного программирования.
Дополнительные трудности при решении оптимальной задачи методами исследования функций классического анализа возникают вследствие того, что система уравнений, получаемая в результате их применения, обеспечивает лишь необходимые условия оптимальности. Поэтому все решения данной системы (а их может быть и несколько) должны быть проверены на достаточность. В результате такой проверки сначала отбрасывают решения, которые не определяют экстремальные значения критерия оптимальности, а затем среди остающихся экстремальных решений выбирают решение, удовлетворяющее условиям оптимальной задачи, т. е. наибольшему или наименьшему значению критерия оптимальности в зависимости от постановки задачи.
Методы исследования при наличии ограничений на область изменения независимых переменных можно использовать только для отыскания экстремальных значений внутри указанной области. В особенности это относится к задачам с большим числом независимых переменных (практически больше двух), в которых анализ значений критерия оптимальности на границе допустимой области изменения переменных становится весьма сложным.
Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и при использовании обычных методов исследования функций, но при наличии ограничений типа равенств на независимые переменные. К требованию возможности получения аналитических выражений для производных от критерия оптимальности при этом добавляется аналогичное требование относительно аналитического вида уравнений ограничений.
В основном при использовании метода множителей Лагранжа приходится решать те же задачи, что и без ограничений. Некоторое усложнение в данном случае возникает лишь от введения дополнительных неопределенных множителей, вследствие чего порядок системы уравнений, решаемой для нахождения экстремумов критерия оптимальности, соответственно повышается на число ограничений. В остальном, процедура поиска решений и проверки их на оптимальность отвечает процедуре решения задач без ограничений.
Множители Лагранжа можно применять для решения задач оптимизации объектов на основе уравнений с частными производными и задач динамической оптимизации. При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных уравнений.
Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их помощью иногда удается снизить размерность решаемой задачи.
Методы вариационного исчисления обычно используют для решения задач, в которых критерии оптимальности представляются в виде функционалов и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации.
Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных ' уравнений Эйлера, каждое из которых является нелинейным дифференциальным уравнением второго порядка с граничными условиями, заданными на обоих концах интервала интегрирования. Число уравнений указанной системы при этом равно числу неизвестных функций, определяемых при решении оптимальной задачи. Каждую функцию находят в результате интегрирования получаемой системы.
Уравнения Эйлера выводятся как необходимые условия экстремума функционала. Поэтому полученные интегрированием системы дифференциальных уравнений функции должны быть проверены на экстремум функционала.
При наличии ограничений типа равенств, имеющих вид функционалов, применяют множители Лагранжа, что дает возможность перейти от условной задачи к безусловной. Наиболее значительные трудности при использовании вариационных методов возникают в случае решения задач с ограничениями типа неравенств.
Заслуживают внимания прямые методы решения задач оптимизации функционалов, обычно позволяющие свести исходную вариационную задачу к задаче нелинейного программирования, решить которую иногда проще, чем краевую задачу для уравнений Эйлера.
Динамическое программирование служит эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых критерий оптимальности задается как аддитивная функция критериев оптимальности отдельных стадий. Без особых затруднений указанный метод можно распространить и на случай, когда критерий оптимальности задан в другой форме, однако при этом обычно увеличивается размерность отдельных стадий.
По существу метод динамического программирования представляет собой алгоритм определения оптимальной стратегии управления на всех стадиях процесса. При этом закон управления на каждой стадии находят путем решения частных задач оптимизации последовательно для всех стадий процесса с помощью методов исследования функций классического анализа или методов нелинейного программирования. Результаты решения обычно не могут быть выражены в аналитической форме, а получаются в виде таблиц.
Ограничения на переменные задачи не оказывают влияния на общий алгоритм решения, а учитываются при решении частных задач оптимизации на каждой стадии процесса. При наличии ограничений типа равенств иногда даже удается снизить размерность этих частных задач за счет использования множителей Лагранжа. Применение метода динамического программирования для оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации приводит к решению дифференциальных уравнений в частных производных. Вместо решения таких уравнений зачастую значительно проще представить непрерывный процесс как дискретный с достаточно большим числом стадий. Подобный прием оправдан особенно в тех случаях, когда имеются ограничения на переменные задачи и прямое решение дифференциальных уравнений осложняется необходимостью учета указанных ограничений.
При решении задач методом динамического программирования, как правило, используют вычислительные машины, обладающие достаточным объемом памяти для хранения промежуточных результатов решения, которые обычно получаются в табличной форме.
Принцип максимума применяют для решения задач оптимизации процессов, описываемых системами дифференциальных уравнений. Достоинством математического аппарата принципа максимума является то, что решение может определяться в виде разрывных функций; это свойственно многим задачам оптимизации, например задачам оптимального управления объектами, описываемыми линейными дифференциальными уравнениями.
Нахождение оптимального решения при использовании принципа максимума сводится к задаче интегрирования системы дифференциальных уравнений процесса и сопряженной системы для вспомогательных функций при граничных условиях, заданных на обоих концах интервала интегрирования, т. е. к решению краевой задачи. На область изменения переменных могут быть наложены ограничения. Систему дифференциальных уравнений интегрируют, применяя обычные программы на цифровых вычислительных машинах.
Принцип максимума для процессов, описываемых дифференциальными уравнениями, при некоторых предположениях является достаточным условием оптимальности. Поэтому дополнительной проверки на оптимум получаемых решений обычно не требуется.
Для дискретных процессов принцип максимума в той же формулировке, что и для непрерывных, вообще говоря, несправедлив. Однако условия оптимальности, получаемые при его применении для многостадийных процессов, позволяют найти достаточно удобные алгоритмы оптимизации.
Линейное программирование представляет собой математический аппарат, разработанный для решения оптимальных задач с линейными выражениями для критерия оптимальности и линейными ограничениями на область изменения переменных. Такие задачи обычно встречаются при решении вопросов оптимального планирования производства с ограниченным количеством ресурсов, при определении оптимального плана перевозок (транспортные задачи) и т. д.
Для решения большого круга задач линейного программирования имеется практически универсальный алгоритм - симплексный метод, позволяющий за конечное число итераций находить оптимальное решение подавляющего большинства задач. Тип используемых ограничений (равенства или неравенства) не сказывается на возможности применения указанного алгоритма. Дополнительной проверки на оптимальность для получаемых решений не требуется. Как правило, практические задачи линейного программирования отличаются весьма значительным числом независимых переменных. Поэтому для их решения обычно используют вычислительные машины, необходимая мощность которых определяется размерностью решаемой задачи.
Методы нелинейного программирования применяют для решения оптимальных задач с нелинейными функциями цели. На независимые переменные могут быть наложены ограничения также в виде нелинейных соотношений, имеющих вид равенств или неравенств. По существу методы нелинейного программирования используют, если ни один из перечисленных выше методов не позволяет сколько-нибудь продвинуться в решении оптимальной задачи. Поэтому указанные методы иногда называют также прямыми методами решения оптимальных задач.
Для получения численных результатов важное место отводится нелинейному программированию и в решении оптимальных задач такими методами, как динамическое программирование, принцип максимума и т. п. на определенных этапах их применения.
Названием “методы нелинейного программирования” объединяется большая группа численных методов, многие из которых приспособлены для решения оптимальных задач соответствующего класса. Выбор того или иного метода обусловлен сложностью вычисления критерия оптимальности и сложностью ограничивающих условий, необходимой точностью решения, мощностью имеющейся вычислительной машины и т.д. Ряд методов нелинейного программирования практически постоянно используется в сочетании с другими методами оптимизации, как, например, метод сканирования в динамическом программировании. Кроме того, эти методы служат основой построения систем автоматической оптимизации - оптимизаторов, непосредственно применяющихся для управления производственными процессами.
Геометрическое программирование есть метод решения одного специального класса задач нелинейного программирования, в которых критерий оптимальности и ограничения задаются в виде позиномов - выражений, представляющих собой сумму произведений степенных функций от независимых переменных. С подобными задачами иногда приходится сталкиваться в проектировании. Кроме того, некоторые задачи нелинейного программирования иногда можно свести к указанному представлению, используя аппроксимационное представление для целевых функций и ограничений.
Специфической особенностью методов решения оптимальных задач (за исключением методов нелинейного программирования) является то, что до некоторого этапа оптимальную задачу решают аналитически, т. е. находят определенные аналитические выражения, например, системы конечных или дифференциальных уравнений, откуда уже отыскивают оптимальное решение. В отличие от указанных методов при использовании методов нелинейного программирования, которые, как уже отмечалось выше, могут быть названы прямыми, применяют информацию, получаемую при вычислении критерия оптимальности, изменение которого служит оценкой эффективности того или иного действия.
Важной характеристикой любой оптимальной задачи является ее размерность n, равная числу переменных, задание значений которых необходимо для однозначного определения состояния оптимизируемого объекта. Как правило, решение задач высокой размерности связано с необходимостью выполнения большого объема вычислений. Ряд методов (например, динамическое программирование и дискретный принцип максимума) специально предназначен для решения задач оптимизации процессов высокой размерности, которые могут быть представлены как многостадийные процессы с относительно невысокой размерностью каждой стадии.
В таблице дана характеристика областей применения различных методов оптимизации, при этом за основу положена сравнительная оценка эффективности использования каждого метода для решения различных типов оптимальных задач. Классификация задач проведена по следующим признакам:
- вид математического описания процесса;
- тип ограничений на переменные процесса
- число переменных.
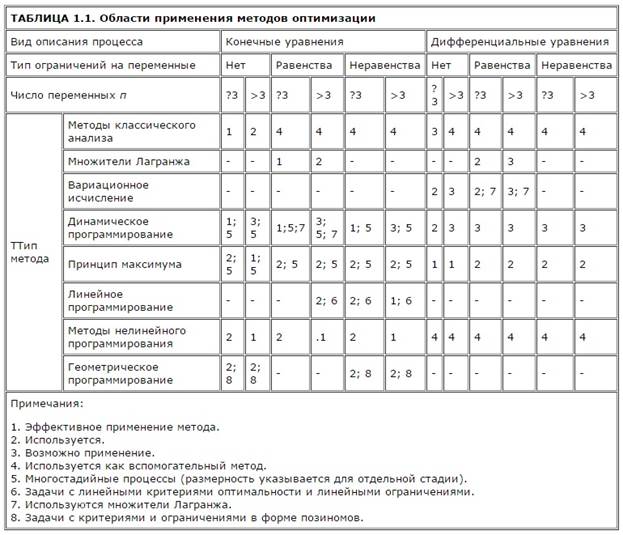
Предполагается, что решение оптимальной задачи для процессов, описываемых системами конечных уравнений, определяется как конечный набор значений управляющих воздействий (статическая оптимизация процессов с сосредоточенными параметрами), а для процессов, описываемых системами обыкновенных дифференциальных уравнений, управляющие воздействия характеризуются функциями времени (динамическая оптимизация процессов с сосредоточенными параметрами) или пространственных переменных (статическая оптимизация процессов с распределенными параметрами).
Классификация задач по группам с числом независимых переменных, большим и меньшим трех или равным трем как характеристика размерности задач с большим и малым числом переменных, разумеется, весьма условна и в данном случае выбрана скорее из соображений наглядности графического изображения пространства изменения переменных задачи - фазового пространства (при числе переменных большем трех графическое изображение фазового пространства обычными приемами отсутствует). Тем не менее, такая классификация до некоторой степени все же отражает действительные трудности, возникающие при решении задач с размерностью выше трех.
