Математические модели силового трансформатора
Рассмотрим математические модели силовых трансформаторов, которые применяются в задачах, связанных с расчетом установившихся режимов схем электрических сетей. В таких моделях не учитываются емкостные связи между витками каждой из обмоток, между самими обмотками и обмотками и землей, а также распределенность электрических и магнитных параметров. Кроме того, ограничимся рассмотрением симметричных режимов нагрузки трансформаторов.
Получим математическую модель однофазного двухобмоточного трансформатора. Вначале предположим, что трансформатор не имеет магнитопровода (воздушный трансформатор), тогда он может быть представлен схемой рис. 2.9, в которой активные сопротивления обмоток изображены отдельно. Полярности обмоток на схеме отмечены звездочками.
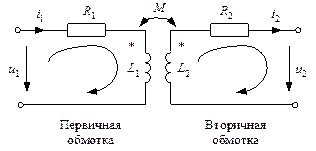
Рис. 2.9. Схема трансформатора без магнитопровода
При обходе контуров на схеме рис. 2.9 в соответствии с заданными направлениями по второму закону Кирхгофа получим уравнения трансформатора в дифференциальной форме:
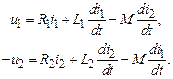
Так как направления токов на схеме ориентированы не одинаково по отношению к звездочкам, то полярность 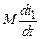 не совпадает с i2 и, наоборот, полярность
не совпадает с i2 и, наоборот, полярность 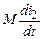 не совпадает с i1.
не совпадает с i1.
При синусоидальных токах и напряжениях уравнения (2.34) в комплексной форме записываются следующим образом:
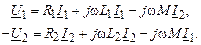
Эти уравнения равносильны следующим:
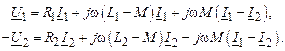
Последним уравнениям соответствует схема замещения рис. 2.10. В отличие от рис. 2.9 в схеме замещения первичная и вторичная цепи трансформатора связаны не индуктивно, а гальванически.
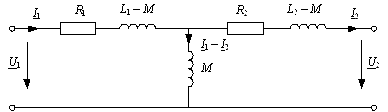
Рис. 2.10. Схема замещения трансформатора без магнитопровода
Входящие в схему рис. 2.10 разности L1 – M и L2 – M имеют физический смысл только при одинаковом числе витков первичной w1 и вторичной w2 обмоток (w1 = w2). В этом случае они представляют собой индуктивности рассеяния Ls1 и Ls2 первичной и вторичной обмоток трансформатора.
В реальных трансформаторах для моделирования потерь в стали в схему замещения трансформатора вводят активную проводимость Gμ. Для моделирования эффекта намагничивания сердечника вводят реактивную проводимость Bμ.
Если взять за основу математической модели трансформатора так называемый идеальный трансформатор с коэффициентом трансформации 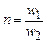 , для которого относительная магнитная проницаемость равна бесконечности и ток намагничивания равен нулю, то добавлением к нему элементов, учитывающих основные паразитные эффекты, можно получить полную схему замещения трансформатора (рис 2.11).
, для которого относительная магнитная проницаемость равна бесконечности и ток намагничивания равен нулю, то добавлением к нему элементов, учитывающих основные паразитные эффекты, можно получить полную схему замещения трансформатора (рис 2.11).
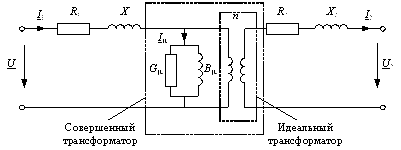
Рис. 2.11. Полная Т-образная схема замещения трансформатора
Потери энергии в обмотках трансформатора при протекании по ним токов учитываются активными сопротивлениями R1 и R2, последовательно с ними включены индуктивности рассеяния, которые учитывают эффект запасания энергии и наведения напряжения в обмотках от потоков рассеяния. Этим индуктивностям соответствуют индуктивные сопротивления обмоток X1 и X2. Ток намагничивания обусловливает намагничивающую силу, которая создает поток взаимной индукции. Величина тока намагничивания Iµ пропорциональна напряжению первичной обмотки. Параллельно индуктивной проводимости намагничивания Bµ включают активную проводимость Gµ, учитывающую потери в сердечнике.
Таким образом, идеальным трансформатором является трансформатор, для которого при любых условиях 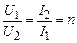 .
.
Трансформатор, для которого при любой нагрузке 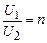 , называется совершенным трансформатором (рис. 2.11).
, называется совершенным трансформатором (рис. 2.11).
Во многих случаях пользуются приведенной Т-образной схемой замещения трансформатора (рис 2.12). Получается она приведениям сопротивлений вторичной обмотки к напряжению первичной обмотки по соотношениям:
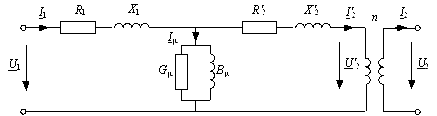
Рис. 2.12. Приведенная Т-образная схема замещения трансформатора
На схеме рис. 2.12 отмечены ток и напряжение:
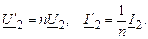
2.2.4. Г-образная и П-образная схемы замещения
силового трансформатора
Обычно для силовых трансформаторов более целесообразна так называемая Г-образная схема замещения, элементы которой имеют простой физический смысл и могут быть вычислены или измерены. Получается она следующим образом.
Ветвь намагничивания переносится на зажимы первичной обмотки и оказывается включенной на напряжение U1. Это вносит погрешность в математическую модель, так как в действительности ток намагничивания (ток холостого хода) протекает по первичной обмотке. Обычно ток холостого хода силовых трансформаторов меньше одного процента от номинального тока трансформатора, и такое упрощение считается допустимым. Сопротивления первичной обмотки оказываются последовательно включенными с приведенными сопротивлениями вторичной обмотки, и при их сложении получаются так называемые сопротивления трансформатора Rт и Xт (рис. 2.13):
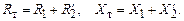

Рис. 2.13. Г-образная схема замещения трансформатора
Полученная схема носит название Г-образной схемы замещения трансформатора и применяется для выполнения расчетов схем электрических сетей, где она еще больше упрощается посредством представления ветви холостого хода в виде постоянных величин потерь активной и реактивной мощности на холостой ход (рис 2.14).
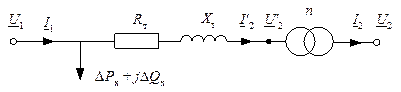
Рис. 2.14. Упрощенная Г-образная схема замещения трансформатора
Все полученное выше для однофазных трансформаторов можно распространить на каждую фазу трехфазного трансформатора.
Сопротивления и проводимости Г-образной схемы замещения трансформатора, приведенные к напряжению обмотки первичного напряжения, определяются по формулам:
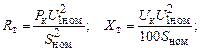
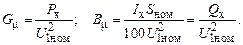
Моделирование элементов схем электрических сетей при использовании специальных программ для расчета их режимов работы удобно выполнять по П-образным схемам замещения. Такую схему замещения можно получить и для трансформатора.
Получим параметры П-образной схемы замещения (см. рис. 2.6) на основе Г-образной схемы замещения двухобмоточного понижающего трансформатора с коэффициентом трансформации n > 1 (рис. 2.13).
Найдем напряжение и ток первичной обмотки:
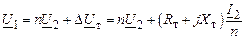 ,
,
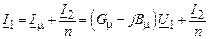 .
.
После подстановки (2.39) в (2.40) получим
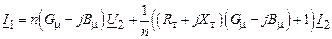 .
.
Сопоставляя выражения (2.39) и (2.41) с уравнениями четырехполюсника
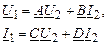
и учитывая соотношения между коэффициентами четырехполюсника и параметрами П-образной схемы замещения [см. (2.22)]:
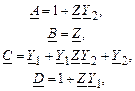
будем иметь:
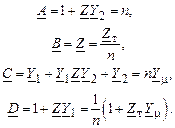
Из полученных соотношений можно найти параметры П-образной схемы замещения трансформатора:
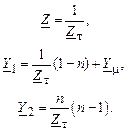
П-образная схема замещения трансформатора в отличие от П-об-разной схемы замещения ЛЭП является несимметричной, т. е. Y1 ≠ Y2.
2.2.5. Построение внешней характеристики
трансформатора
Внешней характеристикой трансформатора называют зависимость изменения вторичного напряжения U2 от тока нагрузки I2 при постоянном коэффициенте мощности приемника cos φ = const и номинальном первичном напряжении U1 = Uном. Сопоставляя внешние характеристики, полученные для различных математических моделей трансформатора, с экспериментально найденной характеристикой трансформатора, можно оценить величину погрешности различных моделей и определить, таким образом, область их использования.
Построим внешнюю характеристику силового трансформатора по его математической модели при изменении тока вторичной обмотки
от нуля до Iном для трех различных коэффициентов мощности: 0,8; 0,9 и 1,0.
Внешнюю характеристику U2 = f(I2) построим по уравнению
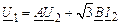 .
.
Примем U1 = U1 = const (совместим с вещественной осью), тогда векторная диаграмма токов и напряжений трансформатора будет иметь вид, как на рис. 2.15.
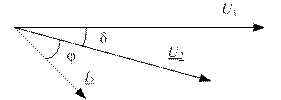
Рис. 2.15. Векторная диаграмма токов и напряжений 1
Выразим из (2.46) напряжение U2:
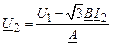 .
.
Здесь ток I2 имеет угол сдвига относительно вещественной оси –(δ + φ), а напряжение вторичной обмотки представлено в комплексном виде: |U2| и δ, где δ входит в левую часть уравнения: U2 = U2e–jδ и в правую: I2 = I2e–j(φ + δ).
Чтобы получить зависимость величины (модуля) U2 от величины (модуля) I2, необходимо перейти к уравнениям с вещественными переменными. Для удобства примем совмещенным с действительной осью вектор U2, тогда векторная диаграмма токов и напряжений примет вид, показанный на рис. 2.16.

Рис. 2.16. Векторная диаграмма токов и напряжений 2
Тогда напряжение U2:
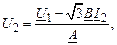
где U1 = U1ejδ; I2 = I2e–jφ.
Разделим уравнение (2.48) на два уравнения с вещественными переменными. С учетом A = A = n и B = B' + jB'' будем иметь систему уравнений:
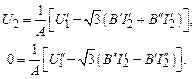
Так как 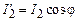 ,
, 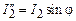 и
и 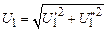 , то получаем систему уравнений
, то получаем систему уравнений
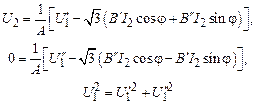
с неизвестными U2, U1′ и U1′′.
Изменяя ток I2 в пределах от нуля до I2ном, будем искать решение системы уравнений (2.50) для каждого значения I2 и строить зависимость U2 = f(I2).
В Mathcad имеется возможность определения функции как решения системы уравнений. Для этого выражение с Find имеет вид определения функции: f(x) := Find(x) и далее в документе Mathcad f(x) становится определенной и является функцией аргумента x.
В нашем случае аргументами функции с Find будет U2 (по условию с углом равным нулю) и cos φ, который также будет различным для разных выходных характеристик.
Пример 1.Определим функцию как решение системы уравнений.
Для удобства записи введем еще две переменные I'2 = I2 cos φ и I''2 = I2 sin φ.
Начальные приближения:
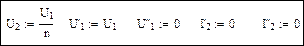
Решающий блок Mathcad:
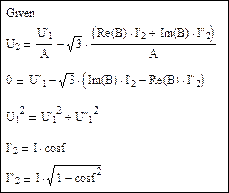
Функция как решение системы уравнений:
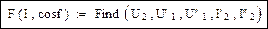
Здесь функция F является вектор-функцией, т. е. содержит пять элементов (по числу неизвестных). Первый элемент дает функцию U2, второй – U′1 и т. д. Нас интересует только первый элемент: функция U2 от I2 и cos φ. Если переменная ORIGIN в Mathcad имеет заданное по умолчанию значение 0, то наша функция будет использоваться в виде F(I2, cosφ)0. Так, например, для cos φ = 0,8 выходная характеристика будет строиться по функции F(I2, 0.8)0 при изменении тока от 0 до Iном.
Пример 2.Построим внешнюю характеристику силового трансформатора ТРДЦН-63000/110 по его математической модели – Г-образной схеме замещения.
Расчеты и построение характеристики выполним в Mathcad. Напряжения в киловольтах, мощности в киловольт-амперах, токи в килоамперах, сопротивления в омах, проводимости в сименсах.
Параметры трансформатора:
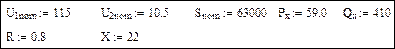
Номинальный ток, коэффициент трансформации и параметры ветви намагничивания:
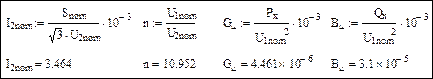
Коэффициенты А и В четырехполюсника:
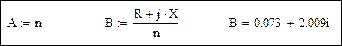
Условия построения характеристики:
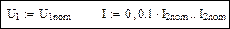
Начальные приближения:
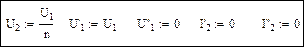
Решающий блок Mathcad:
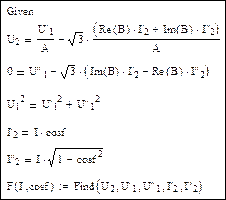
Внешние характеристики для трех значений коэффициента мощности: 1; 0,9 и 0,8:
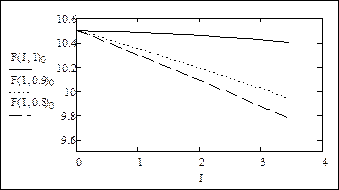
Снижение напряжения на вторичной обмотке с ростом тока нагрузки вызвано потерей напряжения в сопротивлениях обмоток трансформатора. Для того чтобы не допустить снижения напряжения у потребителей электроэнергии, в силовых трансформаторах предусмотрено специальное устройство – регулятор напряжения, который при росте тока нагрузки изменяет коэффициент трансформации таким образом, чтобы обеспечить необходимое напряжение на шинах вторичного напряжения трансформатора.
Получим внешнюю характеристику трансформатора по его упрощенной модели, в которой не учитываются активные параметры: Rт = 0 и Gµ = 0, и сопоставим полученные характеристики с характеристиками, полученными по полной модели.
Коэффициенты А и В четырехполюсника для упрощенной модели:
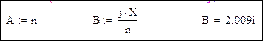
Начальные приближения:
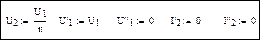
Решающий блок Mathcad:
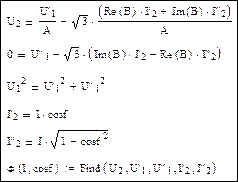
Внешние характеристики для трех значений коэффициента мощности: 1; 0,9 и 0,8:
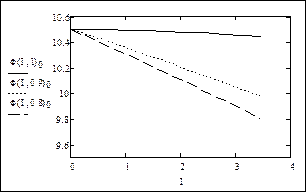
Вычислим и построим функции погрешностей внешних характеристик упрощенной модели:
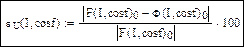
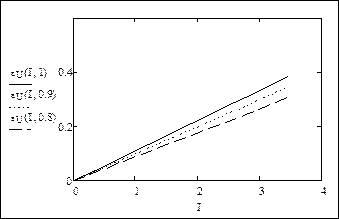
Из последнего рисунка видно, что погрешности характеристик упрощенной модели не превышают 0,4 %. Такая погрешность вполне допустима во многих задачах расчета установившихся режимов и токов короткого замыкания в электрических системах и поэтому иногда активным сопротивлением обмоток трансформатора и потерями в стали пренебрегают. Следует, однако, заметить, что для трансформаторов малой мощности такая картина не сохраняется и применение упрощенной модели становится более ограниченным.
