Необходимые и достаточные условия независимости случайных величин
Теорема:Для того, чтобы случайные величины Х, Y были независимыми, необходимо и достаточно, чтобы функция распределения системы (Х, Y) была равна произведению функций распределения составляющих: F(x,y)=F1(x) F2(y)
Доказательство: а) Необходимость. Пусть Х и Y независимы. Тогда события X<x и Y<y независимы, следовательно, вероятность совмещения этих событий равна произведению их вероятностей:
P(X<x , Y<y) =P(X<x ) P(Y<y) или F(x,y)=F1(x) F2(y).
б) Достаточность. Пусть F(x,y)=F1(x) F2(y). Отсюда P(X<x , Y<y) =P(X<x ) P(Y<y), т.е. вероятность совмещения событий X<x и Y<y равна произведению вероятностей этих событий. Следовательно, случайные величины X и Y независимы.
Следствие: Для того чтобы непрерывные случайные величины Х и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы (Х,Y) была равна произведению плотностей распределения составляющих: f(x,y)=f1(x) f2(y). Доказательство: а) Необходимость. Пусть Х и Y - независимые непрерывные случайные величины. Тогда (на основании предыдущей теоремы): F(x,y)=F1(x) F2(y). Дифференцируя это равенство по х, а потом по y, имеем: 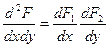 , или (по определению плотностей распределения двумерной и одномерной величин) f(x,y)=f1(x) f2(y).
, или (по определению плотностей распределения двумерной и одномерной величин) f(x,y)=f1(x) f2(y).
б) Достаточность. Пусть f(x,y)=f1(x) f2(y). Интегрируя это равенство по х, а потом по y, получим:
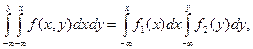 или F(x,y)=F1(x) F2(y). Следовательно, Х и Y независимы.
или F(x,y)=F1(x) F2(y). Следовательно, Х и Y независимы.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики: корреляционный момент и коэффициент корреляции. Корреляционным моментом 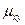 случайных величин Х и Y называют математическое ожидание произведения отклонений этих величин:
случайных величин Х и Y называют математическое ожидание произведения отклонений этих величин: 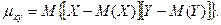 Для вычисления корреляционного момента дискретных величин используют формулу:
Для вычисления корреляционного момента дискретных величин используют формулу: 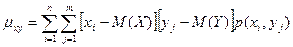 , а для непрерывных величин – формулу:
, а для непрерывных величин – формулу: 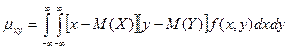 . Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент =0, если X и Y независимы.
. Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент =0, если X и Y независимы.
Теорема: Корреляционный момент двух независимых случайных величин X и Y =0.
Доказательство: Т.к. Х и Y – независимые случайные величины, то их отклонения X-M(X) и Y-M(Y) также независимы. Пользуясь свойствами математического ожидания (мат. ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получаем: 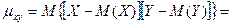
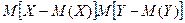 =0. Из определения корреляц.момента следует, что он имеет размерность , равную произведению размерностей величин Х и Y.
=0. Из определения корреляц.момента следует, что он имеет размерность , равную произведению размерностей величин Х и Y.
Коэффициент корреляции rxy случайных величин Х иY - это отношение корреляционного момента к произведению средних квадратических отклонений этих величин: 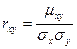 . Так как размерность момента корреляции равна произведению размерностей величин X и Y,
. Так как размерность момента корреляции равна произведению размерностей величин X и Y, 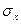 имеет размерность величины X, а
имеет размерность величины X, а 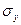 - размерность величины Y, то rxy – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом преимущество коэффициента корреляции перед корреляционным моментом.
- размерность величины Y, то rxy – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом преимущество коэффициента корреляции перед корреляционным моментом.
Теорема: Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий: 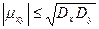 . Доказательство: Введем в рассмотрение случайную величину
. Доказательство: Введем в рассмотрение случайную величину 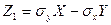 и найдем ее дисперсию D(Z1)=
и найдем ее дисперсию D(Z1)= 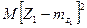 . Выполнив выкладки, получим
. Выполнив выкладки, получим 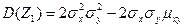 . Любая дисперсия неотрицательна, поэтому
. Любая дисперсия неотрицательна, поэтому 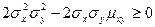 . Отсюда
. Отсюда 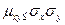 (1). Введя случайную величину
(1). Введя случайную величину 
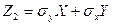 , аналогично найдем
, аналогично найдем 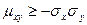 (2). Теперь объединим (1) и(2):
(2). Теперь объединим (1) и(2): 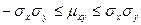 (3) или
(3) или 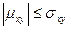 . И таким образом,
. И таким образом, 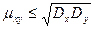 .
.
Теорема:Абсолютная величина коэффициента корреляции не превышает единицы: 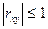 .
.
Доказательство: Разделим обе части двойного неравенства (3) на произведение положительных чисел
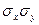 : -1
: -1 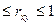 . Итак,
. Итак, 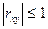 .
.
