Аналитические модели систем массового обслуживания

Аналитическое исследование систем массового обслуживания (СМО) является подходом, альтернативным имитационному моделированию, и состоит в получении формул для расчета выходных параметров СМО с последующей подстановкой значений аргументов в эти формулы в каждом отдельном эксперименте.

В моделях СМО рассматривают следующие объекты:

1) заявки на обслуживание (транзакты);

2) обслуживающие аппараты (ОА), или приборы.

Практическая задача теории массового обслуживания связана с исследованием операций этими объектами и состоит из отдельных элементов, на которые влияют случайные факторы.

В качестве примера задач, рассматриваемых в теории массового обслуживания, можно привести: согласование пропускной способности источника сообщения с каналом передачи данных, анализ оптимального потока городского транспорта, расчет емкости зала ожидания для пассажиров в аэропорту и пр.

Заявка может находиться либо в состоянии обслуживания, либо в состоянии ожидания обслуживания.

Обслуживающий прибор может быть либо занят обслуживанием, либо свободен.

Состояние СМО характеризуется совокупностью состояний обслуживающих приборов и заявок. Смена состояний в СМО называется – событие.

Модели СМО используются для исследования процессов происходящие в системе, при подаче на входы потоков заявок. Эти процессы представляют собой последовательность событий.

Важнейшие выходные параметры СМО

• Производительность

• Пропускная способность

• Вероятность отказа в обслуживании

• Среднее время обслуживания;

• Коэффициент загрузки оборудования (ОА).

Заявками могут быть заказы на производство изделий, задачи, решаемые в вычислительной системе, клиенты в банках, грузы, поступающие на транспортировку и др. Очевидно, что параметры заявок, поступающих в систему, являются случайными величинами и при исследовании или проектировании могут быть известны лишь их законы распределения.

В связи с этим анализ функционирования на системном уровне, как правило, носит статистический характер. В качестве математического аппарата моделирования удобно принять теорию массового обслуживания, а в качестве моделей систем на этом уровне использовать системы массового обслуживания.

Простейшие модели СМО

В простейшем случае СМО представляет собой некоторое устройство, называемое обслуживающим аппаратом (ОА), с очередями заявок на входах.

М о д е л ьо б с л у ж и в а н и я с о т к а з а м и (рис.5.1)

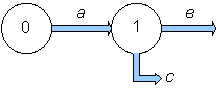Рис. 5.1. Модель СМО с отказами:

0 – источник заявок;

1 – обслуживающий прибор;

а – входной поток заявок на обслуживание;

в – выходной поток обслуженных заявок;

с – выходной поток необслуженных заявок.

В этой модели отсутствует накопитель заявок на входе ОА. Если заявка приходит от источника 0 в момент времени, когда ОА занят обслуживанием предыдущей заявки, то вновь пришедшая заявка выходит из системы (так как ей отказано в обслуживании) и теряется (поток с).

М о д е л ь о б с л у ж и в а н и я с о ж и д а н и е м (рис. 5.2)

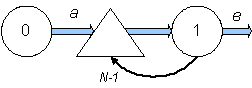
Рис. 5.2. Модель СМО с ожиданием

(N–1) – количество заявок, которое может поместиться в накопителе

В этой модели имеется накопитель заявок на входе ОА. Если заявка приходит от источника 0 в момент времени, когда ОА занят обслуживанием предыдущей заявки, то вновь пришедшая заявка попадает в накопитель, где неограниченно долго ожидает, пока освободится ОА.

М о д е л ь о б с л у ж и в а н и я с о г р а н и ч е н н ы м в р е м е н е м

о ж и д а н и я (рис. 5.3)

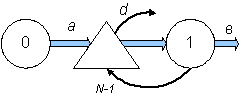Рис. 5.3. Модель СМО с ограниченным временем ожидания:

d – поток заявок, покидающих систему при превышении времени ожидания

В этой модели, как и в предыдущей, имеется накопитель заявок на входе ОА, но время нахождения заявки в накопителе ограничено некоторой величиной.

М н о г о к а н а л ь н а я м о д е л ь СМО с о т к а з а м и (рис. 5.4).

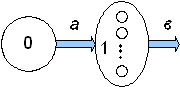Рис. 5.4. Многоканальная модель СМО с отказами:

n – количество одинаковых обслуживающих аппаратов (приборов)

В этой модели имеется не один ОА, а несколько. Заявки, если это специально не оговорено, могут поступать к любому свободному от обслуживания ОА. Накопителя нет, поэтому данная модель включает свойства модели, показанной на рис. 5.1: отказ в обслуживании заявки означает ее безвозвратную потерю (это происходит только в том случае, если в момент прихода этой заявки все ОА заняты).

М н о г о к а н а л ь н а я м о д е л ь СМО с о г р а н и ч е н н ы м

в р е м е н е м о ж и д а н и я (рис. 5.5)

Рис. 5.5. Многоканальная модельСМО с ограниченным временем ожидания

Эта модель объединяет в себе свойства моделей, представленных на рис. 5.3. и 5.4.

М н о г о к а н а л ь н а я м о д е л ь СМО с о ж и д а н и е м

и в о с с т а н о в л е н и е м о т к а з а в ш и х ОА (рис. 5.6)

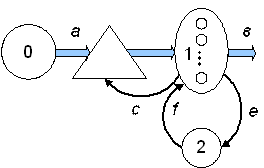Рис. 5.6. Многоканальная модельСМО с ожиданием и восстановлением ОА:

e – обслуживающие аппараты, вышедшие из строя;

f – восстановленные обслуживающие аппараты

Данная модель обладает свойствами моделей, представленных на рис. 5.2 и 5.4, а кроме того свойствами, позволяющими учитывать возможные случайные отказы ОА, которые в этом случае поступают в ремонтный блок 2, где пребывают в течение случайных промежутков времени, затрачиваемых на их восстановление, а затем вновь возвращаются в обслуживающий блок 1.

М н о г о к а н а л ь н а я м о д е л ь СМО с о г р а н и ч е н н ы м

в р е м е н е м о ж и д а н и я и в о с с т а н о в л е н и е м ОА (рис. 5.7)

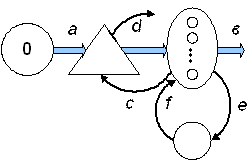Рис. 5.7. Многоканальная модель СМО с ограниченным временем ожидания и восстановлением ОА

Данная модель является довольно сложной, поскольку одновременно учитывает свойства двух не самых простых моделей (рис. 5.5 и 5.6).