Метод Ньютона (метод дотичних)
ЛАБОРАТОРНА РОБОТА № 1
ТЕМА: Методи розв’язання алгебраїчних і трансцендентних рівнянь
Розв’язання рівнянь – алгебраїчних і трансцендентних – являє собою одну з істотних задач прикладного аналізу, потреба в якій виникає в найрізноманітніших розділах фізики, техніки і природознавства.
Задача визначення кореня рівняння з одним невідомим
ƒ(x) = 0 , (1.1)
де ƒ(x) – безперервна функція, складається з двох етапів:
1) відділення кореня, тобто визначення числового проміжку, у якому міститься один корінь рівняння;
2) уточнення значення кореня шляхом побудови послідовності
xк = φ(xк-1) , к = 1, 2, 3, ...
на основі відповідного методу.
Для уточнення значення кореня існують різні ітераційні методи.
1.1 Відділення числового проміжку, у якому міститься один корінь рівняння
1.1.1 Відділення кореня графічно (перший спосіб)
Якщо рівняння (1.1) зручно представити у вигляді
g (х) – h (х) , (1.2)
то абсцису х0 точки перетинання графіків у = g(х) і у = h(х) можна знайти по кресленню.
Величину х0 визначити з достатньою точністю графічно не можливо. Тому варто вибрати такий числовий проміжок [a ; b] для якого свідомо виконується нерівність a ≤ х0 ≤ b .
Різні знаки функції при х =а і х = b
ƒ(а) * ƒ(b) ≤ 0 (1.3)
свідчать про наявність кореня в проміжку [a ; b] .
1.1.2 Другий спосіб відділення кореня
Цей спосіб містить звичайне табулювання функції у = ƒ(х) на інтервалі існування функції, при цьому ступінь зміни аргументу підбирається значимим. І знову, різні знаки функції при х =а і х = b , тобто ƒ(а) * ƒ(b) ≤ 0 свідчать про наявність кореня в проміжку [a ; b].
1.2 Уточнення значення кореня рівняння ƒ(x) = 0
1.2.1 Метод половинного ділення (метод бісекцій)
Умова застосовності методу половинного ділення припускає безперервність функції ƒ(х) на проміжку [a ; b].
Уточнення значення кореня проводиться шляхом побудови послідовності, що сходиться
xк =(ак + bк) / 2 , к = 1, 2, (1.4)
За а1 , b1 приймаємо відповідно а , b .
Припускаючи, що наближення xn (де n – фіксоване значення к ) відомо, для знаходження xn+1 вибираємо наступні значення an+1 , bn+1 в залежності від знака добутку f(an ) * f(xn ) .
Якщо f(an ) * f(xn ) < 0 , то bn+1 вважаємо рівним знайденому значенню xn і an+1 рівними an , інакше bn+1 = bn , an+1 = xn .
На рис. 1.1 зображена поведінка послідовних наближень у випадку ƒ(а) < 0 , ƒ(b) > 0 .
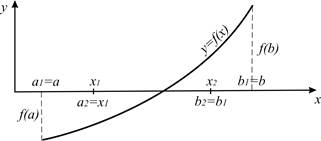
Рисунок 1.1 – Графічне зображення методу бісекцій
Рішення рівняння (1.1) вважається знайденим з точністю Е , якщо виконається умова
| хк + 1 – хк | < Е (1.5)
1.2.2 Метод хорд (метод пропорційних чисел)
Умови збіжності методу припускають, що ƒ'(x) і ƒ''(x) зберігають знак на проміжку [a ; b] .
Побудова послідовності, що сходиться, проводиться по формулі
хк = хк – 1 - ƒ(хк – 1) * (с - хк – 1) / (ƒ(с) - ƒ(хк – 1)) , к = 1, 2, ... (1.6)
де с – нерухомий кінець проміжку.
Якщо ƒ(а) * ƒ''(а) > 0 , то за нерухомий кінець приймається а , тоді х0 = b .
У противному випадку, нерухомий кінець b , а як нульове наближення вибирається а .
На рис. 1.2 зображене поводження послідовних наближень у випадках:
а) ƒ(а) > 0 , ƒ''(а) > 0 ; б) ƒ(а) < 0 , ƒ''(а) < 0 .
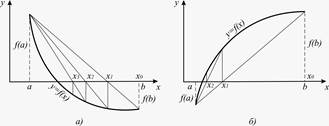
Рисунок 1.2 – Графічне зображення методу хорд (послідовні наближення)
Процес наближення відбувається до виконання умови (1.5) , або доки ƒ(хк) | ≤ Е (1.7)
Метод Ньютона (метод дотичних)
Умови збіжності методу припускають, що ƒ'(x) і ƒ''(x) зберігають знак на проміжку [a ; b] .
Уточнення значення кореня проводиться шляхом побудови збіжності послідовності.
хк = хк – 1 - ƒ(хк – 1) / ƒ'(хк – 1) , к = 1, 2, 3,... (1.8)
За х0 приймаємо той з кінців проміжку [a ; b] , на якому виконується умова
ƒ(х0) * ƒ''(х0) > 0 (1.9)
Поведінка послідовних наближень при ƒ(а) < 0 , ƒ''(а) < 0 (а) ; ƒ(а) > 0 , ƒ''(а) > 0 (б) ілюструється на рис. 1.3 .
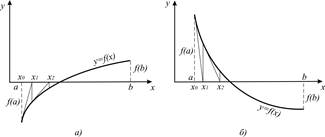
Рисунок 1.3 – Графічне відображення методу дотичних
Процес наближення відбувається до виконання умови (1.5) , або (1.7).
1.2.4 Використання пакету аналізу „что - если” Excel
Чисельний аналіз даних зазвичай відбувається через меню „Сервис” . Інструмент „Подбор параметра” дозволяє знайти значення аргументу, задовольняючого наданому значенню функції. Якщо необхідно вирішити рівняння ƒ(x) = 0 , треба визначити адресу клітини, куди буде занесене початкове значення кореня. Саме рівняння ƒ(x) записується в іншій клітині з посиланням на першу. У вікні „Подбор параметра” вказуємо початкові значення параметрів, зразок на рис.1.4.
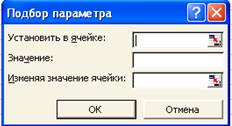
Рисунок 1.4 – Вікно „Подбор параметра”
Для уточнювання знайденого рішення потрібно в меню „Сервис / Параметри” на вкладниці „Вычисления” змінити значення відповідних параметрів: кількість ітерацій; погрішність.
1.3 Індивідуальні завдання
Для кожної функції визначити числовий проміжок у якому міститься один корінь рівняння, уточнити значення кореня вказаними вище методами.
1.3.1 1.3.2
1) 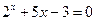 ; 1)
; 1) 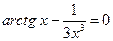 ;
;
2) 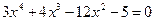 ; 2)
; 2) 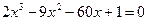 ;
;
3) 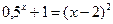 ; 3)
; 3) 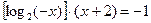 ;
;
4) 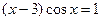 ,
, 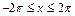 . 4)
. 4) 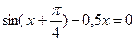 .
.
1.3.3 1.3.4
1) 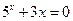 ; 1)
; 1) 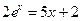 ;
;
2) 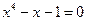 ; 2)
; 2) 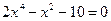 ;
;
3) 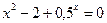 ; 3)
; 3) 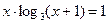 ;
;
4) 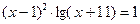 . 4)
. 4) 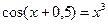 .
.
1.3.5 1.3.6
1) 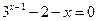 ; 1)
; 1) 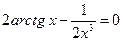 ;
;
2) 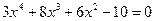 ; 2)
; 2) 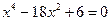 ;
;
3) 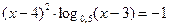 ; 3)
; 3) 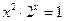 ;
;
4) 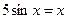 . 4)
. 4) 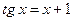 ,
, 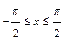 .
.
1.3.7 1.3.8
1) 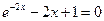 ; 1)
; 1) 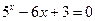 ;
;
2) 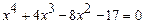 ; 2)
; 2) 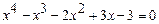
3) 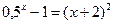 ; 3)
; 3) 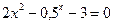 ;
;
4) 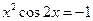 . 4)
. 4) 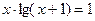 .
.
1.3.9 1.3.10
1) 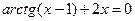 ; 1)
; 1) 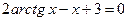 ;
;
2) 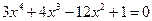 ; 2)
; 2) 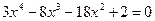 ;
;
3) 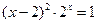 ; 3)
; 3) 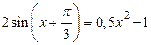 ;
;
4) 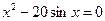 . 4)
. 4) 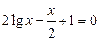 .
.
1.3.11 1.3.12
1) 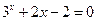 ; 1)
; 1) 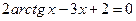 ;
;
2) 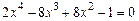 ; 2)
; 2) 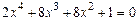 ;
;
3) 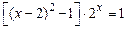 ; 3)
; 3) 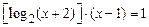 ;
;
4) 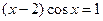 ,
, 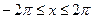 . 4)
. 4) 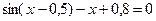 .
.
1.3.13 1.3.14
1) 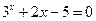 ; 1)
; 1) 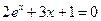 ;
;
2) 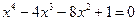 ; 2)
; 2) 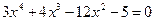 ;
;
3) 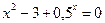 ; 3)
; 3) 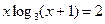 ;
;
4) 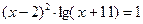 . 4)
. 4) 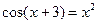 .
.
1.3.15 1.3.16
1) 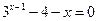 ; 1)
; 1) 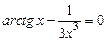 ;
;
2) 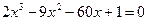 ; 2)
; 2) 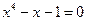 ;
;
3) 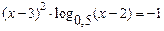 ; 3)
; 3) 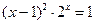 ;
;
4) 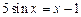 . 4)
. 4) 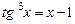 ,.
,. 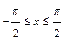
1.3.17 1.3.18
1) 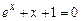 ; 1)
; 1) 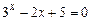 ;
;
2) 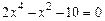 ; 2)
; 2) 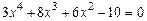 ;
;
3) 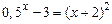 ; 3)
; 3) 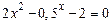 ;
;
4) 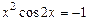 ,
, 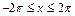 . 4)
. 4) 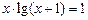 .
.
1.3.19 1.3.20
1) 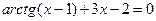 ; 1)
; 1) 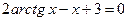 ;
;
2) 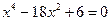 ; 2)
; 2) 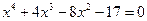 ;
;
3) 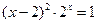 ; 3)
; 3) 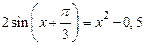 ;
;
4) 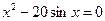 . 4)
. 4) 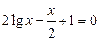 .
.
1.3.21 1.3.22
1) 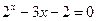 ; 1)
; 1) 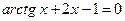 ;
;
2) 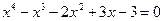 ; 2)
; 2) 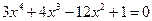 ;
;
3) 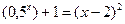 ; 3)
; 3) 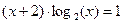 ;
;
4) 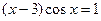 ,
, 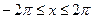 . 4)
. 4) 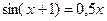 .
.
1.3.23 1.3.24
1) 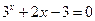 ; 1)
; 1) 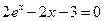 ;
;
2) 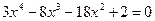 ; 2)
; 2) 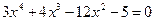 ;
;
3) 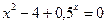 ; 3)
; 3) 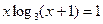 ;
;
4) 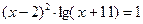 . 4)
. 4) 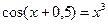 .
.
1.3.25 1.3.26
1) 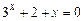 ; 1)
; 1) 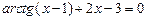 ;
;
2) 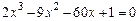 ; 2)
; 2) 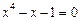 ;
;
3) 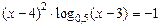 ; 3)
; 3) 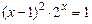 ;
;
4) 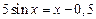 . 4)
. 4) 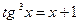 ,
, 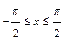 .
.
1.3.27 1.3.28
1) 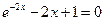 ; 1)
; 1) 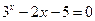 ;
;
2) 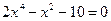 ; 2)
; 2) 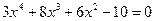 ;
;
3) 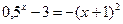 ; 3)
; 3) 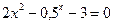 ;
;
4) 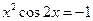 . 4)
. 4) 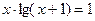 .
.
1.3.29 1.3.30
1) 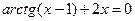 ; 1)
; 1) 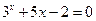 ;
;
2) 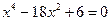 ; 2)
; 2) 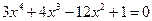 ;
;
3) 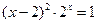 ; 3)
; 3) 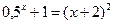 ;
;
4) 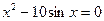 . 4)
. 4) 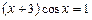 ,
, 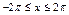
1.4 Приклади виконання лабораторної роботи
Приклад 1.4.1Розв’язати нелінійне рівняння 2 - lg x – x = 0 з точністю ε = 0,001 методом бісекцій.
1) Відокремимо корінь рівняння графічно, для чого дане рівняння представимо у вигляді lg x = - x + 2 .
Побудуємо графіки функцій y = lg x i y = - x + 2 .
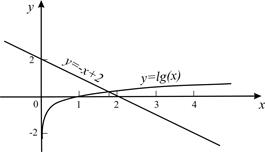
Рисунок 1.5 – Графічне відокремлення кореня рівняння
З рис. 1.5 видно, що шуканий корінь лежить на інтервалі [1 ; 2]. Перевіримо умову ƒ(а) * ƒ(b) < 0 :
ƒ(1) = 2-lg 1 – 1 = 1 > 0
ƒ(2) = 2-lg 2 – 2 ≈ -0,301 < 0 ,
тобто а1 = 1 ; b1 = 2 .
2) Напишемо програму чисельного розв’язання вказаного рівняння методом бісекцій, для чого на „Лист1” Excel помістимо об’єкт – „командна кнопка” з ім’ям CommandButton1 , як показано на рис. 1.6 .
Щоб вбудувати кнопку на Лист, виконайте наступні дії:
1) активізуйте кнопку „Конструктор”  на панелі інструментів Visual Basic;
на панелі інструментів Visual Basic;
2) активізуйте панель „Елементи керування” за допомогою кнопки  .
.
3) клацніть мишею на елементі керування „Кнопка” , а потім клацніть на Лист1 Excel. З’явиться кнопка з написом CommandButton1 .
4) у вікні властивостей „Кнопки” змініть властивості:
− Caption : текст „CommandButton1” на текст „Уточнення методом бісекцій” ;
− Font : зазначений розмір 12 і жирний ;
− Multiline : True ;
− WordWrap : True .
5) щоб зв’язати з подією Click на кнопці процедуру уточнення кореня рівняння методом бісекцій, двічі клацніть на самій кнопці. Відкриється вікно модуля, в якому написано заголовок процедури:
Sub CommandButton1_Click()
Перш, ніж записати відповідну програму, змінимо ім’я листа книги Excel: „Лист1” на „прим1” .

Рисунок 1.6 – Приклад розташування командної кнопки на листі Excel
Текст процедури:
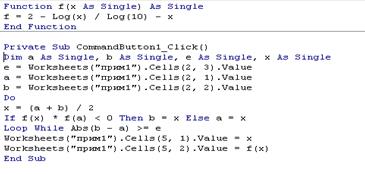
Виходимо із режима „Конструктор” .
Введемо початкові значення для а , b , ε у відповідні клітини листа „прим1” . Натискаючи на командну кнопку, результати уточнювання кореня побачимо також на листі „прим1” , як на рис. 1.7 .
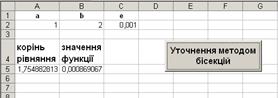
Рисунок 1.7 – Результат обчислень за методом бісекцій
Приклад 1.4.2Розв’язати нелінійне рівняння 2 - lg x – x = 0 з точністю ε = 0,001 методом хорд.
1) Відокремимо корінь рівняння звичайним табулюванням функції на інтервалі [a ; b] в середовищі Excel . Значення а , b підбираємо таким чином, щоб вказана функція існувала і була неперервна. Кількість розподілу інтервалу задаємо такою, щоб шаг (крок) зміни змінної був значимим.
В клітину E2 введемо формулу: = (C2 – B2) / D2 , в B5 : = B2, в B6 : = B5 + $E$2 , в C5 : = 2 – LOG10(B5) – B5 , в клітину А2 введемо значення точності обчислень ε , як показано на рис. 1.8 .
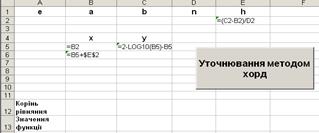
Рисунок 1.8 – Зразок заповнення клітин початковими даними
Таблицю заповнюємо за допомогою маркера заповнення  ↓. Шукаємо проміжок для х , де функція змінює свій знак на протилежний. Якщо такої зміни не відбувається, то достатньо змінити значення а , b в клітинах A2 , B2 . Автоматичний перерахунок в таблиці визначить нові значення функції. Так можна робити доки в таблиці не з’являться різні за знаками значення у . У нашому випадку х є [1,66 ; 2,44] , як показано на рис. 1.9 .
↓. Шукаємо проміжок для х , де функція змінює свій знак на протилежний. Якщо такої зміни не відбувається, то достатньо змінити значення а , b в клітинах A2 , B2 . Автоматичний перерахунок в таблиці визначить нові значення функції. Так можна робити доки в таблиці не з’являться різні за знаками значення у . У нашому випадку х є [1,66 ; 2,44] , як показано на рис. 1.9 .
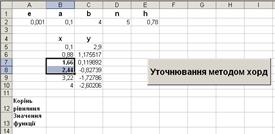
Рисунок 1.9 – Приклад вибору проміжку для х
Як і в попередньому випадку розміщуємо командну кнопку на Лист2 з ім’ям CommandButton1 , змінюємо відповідні властивості: Caption текст „CommandButton1” на текст „Уточнення методом хорд” . Зв’яжемо з подією Click на кнопці процедуру уточнення кореня рівняння методом хорд.
Знайдемо другу похідну :
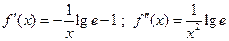 .
.
Створимо дві функції користувача.
Текст процедури:
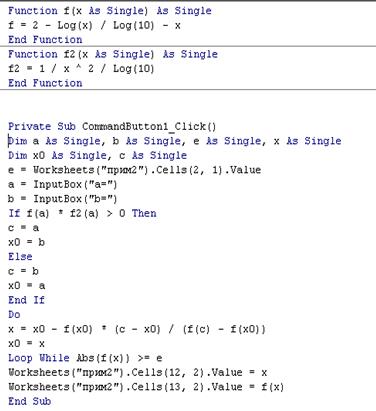
Зразок протоколу рішення наведено на рис. 1.10 .
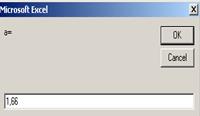
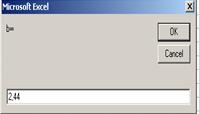
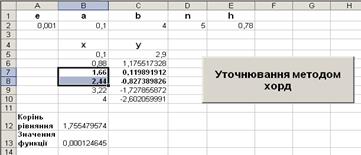
Рисунок 1.10 – Протокол рішення
Приклад 1.4.3Розв’язати нелінійне рівняння 2 - lg x – x = 0 з точністю ε = 0,001 методом дотичних.
1) Відокремимо корінь рівняння одним з двох способів.
2) Створимо форму, в якій розмістимо такі елементи керування:
− Написи Label1 , Label2 , Label3 , Label4 , Label5 , у яких властивості Caption змінені на тексти, зазначені на рис. 1., тобто: eps = , a = , b = , корінь = , значення функції = . Крім того, у написів змінена властивість Font – шрифт, жирность ;
− Текстові поля TextBox1 – для введення значення ε ; TextBox2 , TextBox3 – для введення значень інтервалу а , b ; TextBox4 , TextBox5 – для виведення результатів розрахунку. Також для цих елементів керування змінені властивості Name на te , ta , tb , xk , fun відповідно;
− Командна кнопка CommandButton1 , з якою зв’язується процедура введення та уточнювання кореня методом дотичних. Для неї змінена властивість Caption на текст „Рішення нелінійних рівнянь методом дотичних” .
Зразок форми наведений на рис. 1.11 .
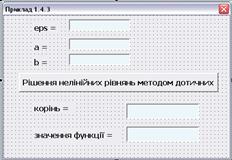
Рисунок 1.11 – Приклад форми
Перш ніж написати процедуру визначимось з похідними:
ƒ(х) = 2 - lg х – х
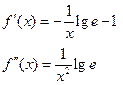
На рис. 1.12 наведена форма в процесі роботи. Користувач повинен ввести числа: eps , a , b в текстові поля і клацнути на кнопці „Уточнення методом дотичних”. Там же з’являться результати роботи програми.
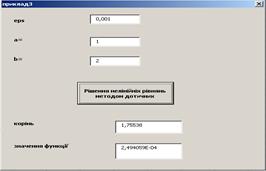
Рисунок 1.12 – Зразок форми в процесі роботи
Текст програми:

Приклад 1.4.4Розв’язати нелінійне рівняння 2 - lg x – x = 0 методами чисельного аналізу Excel.
1) Відокремимо початкове значення кореня рівняння одним з вказаних вище способів.
2) Шукаємо рішення в клітині A2 , заносимо початкове значення кореня, наприклад, 1 , рис. 1.
Саме рівняння запишемо в B2 : = 2 – LOG10(A2) – A2 . Використовуємо меню Сервис / Подбор параметра . У вікні вказуємо аргументи, як на рис. 1.13 .
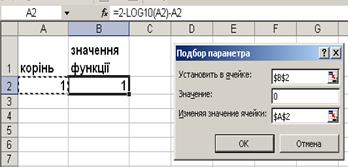
Рисунок 1.13 – Вікно „Подбор параметра”
Рішення побачимо в клітинах A2 та B2 , як показано на рис. 1.14 .
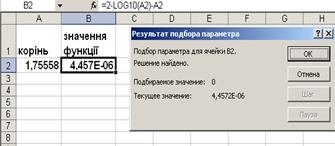
Рисунок 1.14 – Результати обчислень
ЛАБОРАТОРНА РОБОТА № 2
ТЕМА: Методи розв’язання систем нелінійних рівнянь
Розв’язання систем нелінійних рівнянь – важливіша задача прикладного аналізу. Розглянемо методи розв’язання на системі двох рівнянь з двома невідомими:
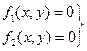 (2.1)
(2.1)
Ця задача складається з двох етапів:
1) відділення кореня, тобто визначення першого наближення до рішення;
2) уточнення значення кореня шляхом побудови відповідної послідовності наближень ітераційними методами.
2.1 Відділення першого наближення до рішення
Відділення початкового наближення можна зробити за допомогою графічних можливостей Excel, якщо систему (2.1) можна представити у вигляді:
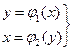 (2.2)
(2.2)
х0 , у0 визначаються як координати точки перетинання цих графіків.
Відокремити початкове наближення х0 , у0 до рішення системи можна із області існування змінних х , у для рівнянь (2.1).
2.2 Методи уточнення рішення системи нелінійних рівнянь
2.2.1 Метод ітерацій
Зведемо систему (2.1) до вигляду
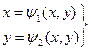 , (2.3)
, (2.3)
по встановленому початковому наближенню до рішення х0 , у0 , уточнення рішення відбувається за формулами:
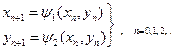 (2.4)
(2.4)
Умови збіжності методу припускають, що
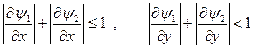 (2.5)
(2.5)
Рішення системи (2.1) вважається знайденим з точністю ε , якщо виконуються умови:
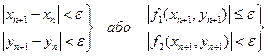
2.2.2 Використання пакету аналізу Excel
Рішення систем нелінійних рівнянь відбувається через меню „Сервис” та інструмент „Поиск решения” .
У вікні „Поиск решения” треба визначитись з адресами цільової функції та адресами, де буде розміщене рішення системи хn+1 , yn+1 .
Вказати за допомогою перемикача значення цільової функції (максимальне, мінімальне чи нульове) . Якщо систему (2.1) можна визначити у вигляді
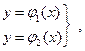 то
то
за цільову функцію вибирають =СРОТКЛ( ; ) - середньоквадратичне відхилення 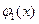 від
від 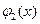 , як показано на рис. 2.1 .
, як показано на рис. 2.1 .
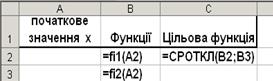
Рисунок 2.1 – Приклад визначення цільової функції
У загальному випадку будують функцію 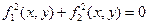 , яку визначають як цільову. Вікно пошуку рішення показано на рис. 2.2 .
, яку визначають як цільову. Вікно пошуку рішення показано на рис. 2.2 .
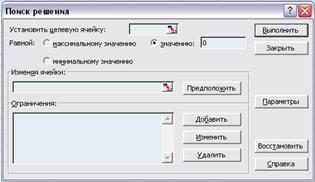
Рисунок 2.2 – Вікно „Поиск решения”
Зверніть увагу, що у групі „Равной” встановлено перемикач в положення „значению” , а в полі вводу вказано значення 0 .
Додатково необхідно у діалоговому вікні „Параметри поиска решения” зняти прапорець біля „Линейная модель” і натиснути на „Выполнить” .
2.3 Індивідуальні завдання
Для кожної системи нелінійних рівнянь визначити початкове наближення до рішення та уточнити це рішення з точністю ε = 0,001 .
2.3.1
1) 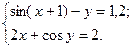 2)
2) 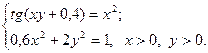
2.3.2
1) 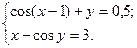 2)
2) 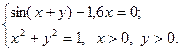
2.3.3
1) 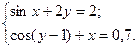 2)
2) 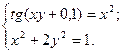
2.3.4
1) 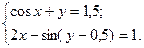 2)
2) 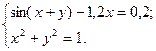
2.3.5
1) 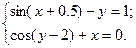 2)
2) 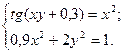
2.3.6
1) 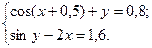 2)
2) 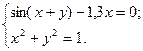
2.3.7
1) 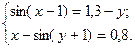 2)
2) 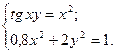
2.3.8
1) 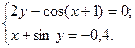 2)
2) 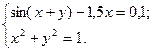
2.3.9
1) 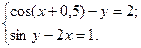 2)
2) 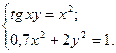
2.3.10
1) 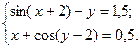 2)
2) 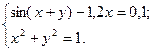
2.3.11
1) 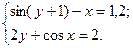 2)
2) 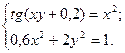
2.3.12
1) 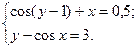 2)
2) 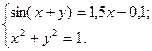
2.3.13
1) 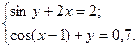 2)
2) 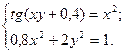
2.3.14
1) 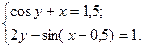 2)
2) 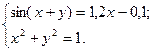
2.3.15
1) 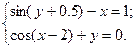 2)
2) 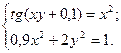
2.3.16
1) 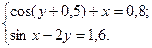 2)
2) 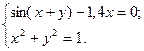
2.3.17
1) 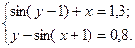 2)
2) 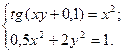
2.3.18
1) 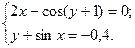 2)
2) 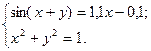
2.3.19
1) 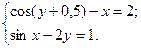 2)
2) 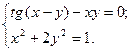
2.3.20
1) 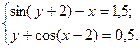 2)
2) 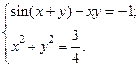
2.3.21
1) 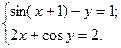 2)
2) 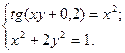
2.3.22
1) 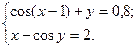 2)
2) 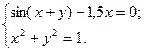
2.3.23
1) 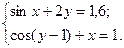 2)
2) 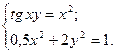
2.3.24
1) 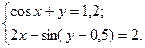 2)
2) 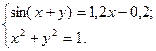
2.3.25
1) 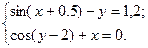 2)
2) 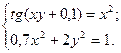
2.3.26
1) 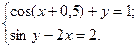 2)
2) 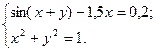
2.3.27
1) 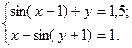 2)
2) 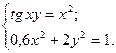
2.3.28
1) 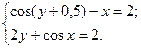 2)
2) 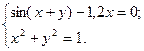
2.3.29
1) 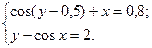 2)
2) 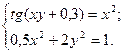
2.3.30
1) 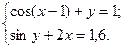 2)
2) 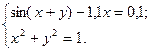
2.4 Приклади виконання лабораторної роботи
Приклад 2.4.1Розв’язати систему нелінійних рівнянь з точністю ε = 0,001 методом ітерацій.
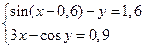 (2.4.1)
(2.4.1)
1) Визначимо початкове наближення графічно, для чого перепишемо систему (2.4.1) у вигляді:
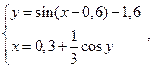
та протабулюємо у середовищі Excel , як показано на рис. 2.3 .
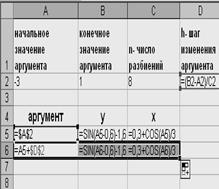
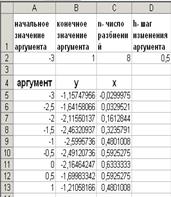
Рисунок 2.3 – Приклад табулювання функції у середовищі Excel
Виділимо дані у стовпчиках А та В , та активізуємо „Майстра діаграм” .
Вибираємо на першому кроці тип діаграми - „точечная” , на другому кроці на вкладинці „Ряд” для ряду 1 змінимо ім’я на у .
У групі „Ряд” натиснемо на кнопку „Добавить” , вкажемо ім’я другої функції х .
У полі для „значення х” вказати діапазон значень стовпчика С , тобто стовпчика, де розміщені відповідні значення другої функції х .
У полі для „значення у” вказати діапазон значень стовпчика А , стовпчика, де розміщені значення у для функції х , зразок наведено на рис. 2.4 .
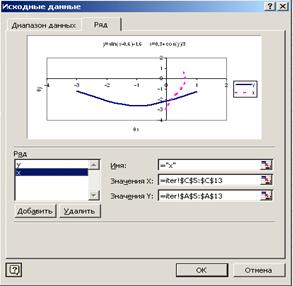
Рисунок 2.4 – Другий крок – вікно „Исходные данные”
Якщо на графіку немає точки перетинання цих функцій, то треба змінити значення стовпчика А .
2) Для уточнювання знайдених х0 , у0 додамо модуль у проект цієї книги, або розмістимо на „Лист1” кнопку CommandButton1 , де запишемо відповідну процедуру.
Надана система має вигляд (2.3). Перевіримо виконання умови збіжності методу ітерацій (2.5) :
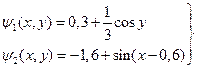
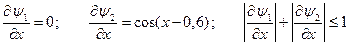
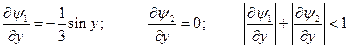
Текст процедури:
Протокол рішення наведено на рис. 2.5 .
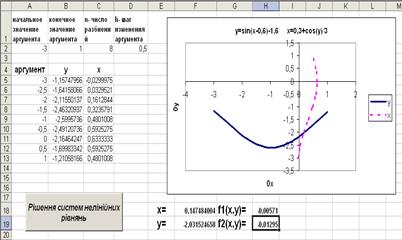
Рисунок 2.5 – Протокол рішення системи
Приклад 2.4.2Розв’язати систему нелінійних рівнянь
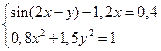 (2.4.2)
(2.4.2)
використовуючи пакет аналізу Excel.
1) Для визначення х0 , у0 протабулюємо функцію в середовищі Excel:
(sin(2x - y) - 1,2x - 0,4)2 + (0,8x2 + 1,5y2 – 1)2 = 0 .
Зразок наведено на рис. 2.6 .
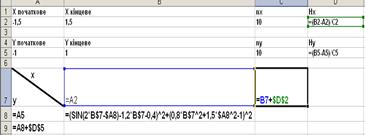
Рисунок 2.6 – Табулювання функції в середовищі Excel
У таблиці знайдемо саме наближене до 0 значення функції. Відповідні йому х, у і будуть визначати х0 ,у0, тобто, х0 = -0,3, у0 = -0,8.
Результат показано на рис. 2.7 .

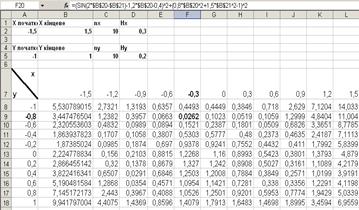
Рисунок 2.7 – Таблиця значень функції
2) Згідно пакету аналізу розмістимо ці значення у відповідних клітинах та запишемо визначену функцію. Використовуючи „Поиск решения” вказуємо адреси, як показано на рис. 2.8 .
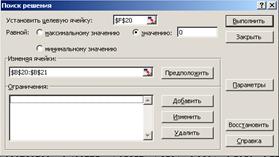
Рисунок 2.8 – Вікно „Поиск решения” з заданими параметрами
Підрахуємо значення системи для знайденого рішення. Відповідні результати показані на рис. 2.9 .

Рисунок 2.9 – Результати обчислень
ЛАБОРАТОРНА РОБОТА № 3
ТЕМА: Обчислення інтегралів
3.1 Теоретичні відомості
Точне обчислення визначеного інтеграла за формулою Ньютона-Лейбниця не завжди представляється можливим чи доцільним. У цих випадках, а також у випадках, коли підінтегральна функція задана табличним способом, доцільно проводити обчислювання приблизно. До найпростіших методів відносяться формула прямокутників, формула парабол (Сімпсона).
При обчисленнях за формулами прямокутників результати будуть тим точніші, чим більше число відрізків розбивки проміжку інтегрування. Найпростіша - формула лівих прямокутників:
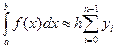 , (3.1)
, (3.1)
де 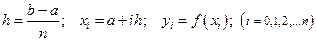
Для забезпечення наданої степені точності ε значення n визначається за умовою:
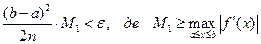 (3.2)
(3.2)
За формулою парабол маємо:
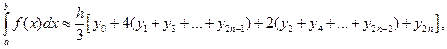 (3.3)
(3.3)
де 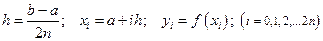
Згідно екстраполяції по Річардсону більш точне значення інтеграла можна визначити за формулою:
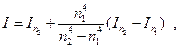 (3.4)
(3.4)
де 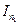 ,
, 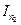 - два наближених значення
- два наближених значення 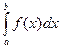 ,знайдених по формулі параболи для n1 та n2 (n2 > n1) .
,знайдених по формулі параболи для n1 та n2 (n2 > n1) .
3.2 Індивідуальні завдання
Для кожного варіанту:
1) обчислити інтеграл по формулі прямокутників з точністю ε = 0,01 ;
2) по формулі парабол обчислити інтеграл, уточнювання провести згідно формулі Річардсона.
3.2.1
1) 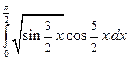 ; 2)
; 2) 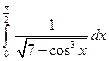 .
.
3.2.2
1) 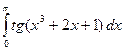 ; 2)
; 2) 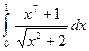 .
.
3.2.3
1) 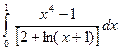 ; 2)
; 2) 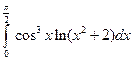 .
.
3.2.4
1) 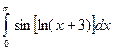 ; 2)
; 2) 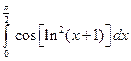 .
.
3.2.5
1) 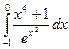 ; 2)
; 2) 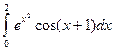 .
.
3.2.6
1) 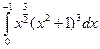 ; 2)
; 2) 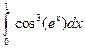 .
.
3.2.7
1) 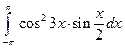 ; 2)
; 2) 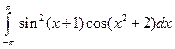 .
.
3.2.8
1) 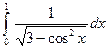 ; 2)
; 2) 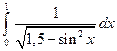 .
.
3.2.9
1) 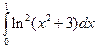 ; 2)
; 2) 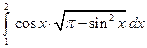 .
.
3.2.10
1) 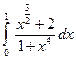 ; 2)
; 2) 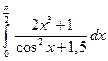 .
.
3.2.11
1) 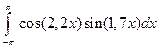 ; 2)
; 2) 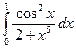 .
.
3.2.12
1) 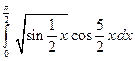 ; 2)
; 2) 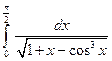 .
.
3.2.13
1) 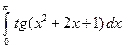 ; 2)
; 2) 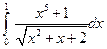 .
.
3.2.14
1) 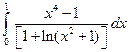 ; 2)
; 2) 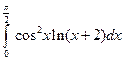 .
.
3.2.15
1) 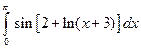 ; 2)
; 2) 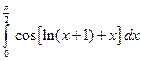 .
.
3.2.16
1) 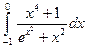 ; 2)
; 2) 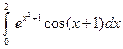 .
.
3.2.17
1) 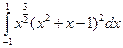 ; 2)
; 2) 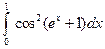 .
.
3.2.18
1) 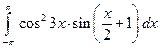 ; 2)
; 2) 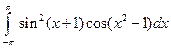 .
.
3.2.19
1) 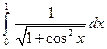 ; 2)
; 2) 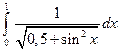 .
.
3.2.20
1) 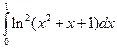 2)
2) 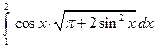 .
.
3.2.21
1) 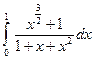 ; 2)
; 2) 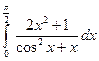 .
.
3.2.22
1) 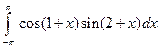 ; 2)
; 2) 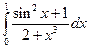 .
.
3.2.23
1) 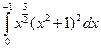 ; 2)
; 2) 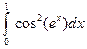 .
.
3.2.24
1) 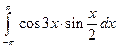 ; 2)
; 2) 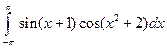 .
.
3.2.25
1) 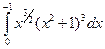 ; 2)
; 2) 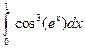 .
.
3.2.26
1) 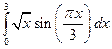 ; 2)
; 2) 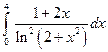 .
.
3.2.27
1) 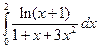 ; 2)
; 2) 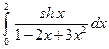 .
.
3.2.28
1) 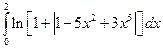 ; 2)
; 2) 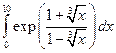 .
.
3.2.29
1) 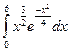 ; 2)
; 2) 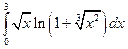 .
.
3.2.30
1) 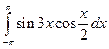 ; 2)
; 2) 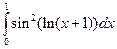 .
.
3.3 Приклади виконання лабораторної роботи
Приклад 3.3.1Обчислити інтеграл 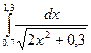 за формулою прямокутників з точністю ε=0,01.
за формулою прямокутників з точністю ε=0,01.
Вирішимо задачу, використовуючи середовище Excel. Треба обчислити функцію 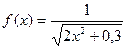 на проміжку [0,7;1,3].
на проміжку [0,7;1,3].
Кількість відрізків розбивки проміжку інтегрування визначимо з умови (3.2) :
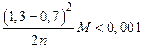 ,
,
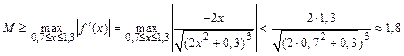 ,
,
М=2, тоді 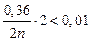 ;
; 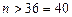 .
.
Розмістимо початкові значення та таблицю значень x, у у такому вигляді, як показано на рис. 3.1 .

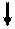

Рисунок 3.1 – Таблиця початкових значень та значень х, у
Згідно протоколу рішення, який показано на рис. 3.2 , отримаємо відповідь: 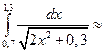 0,406865 .
0,406865 .
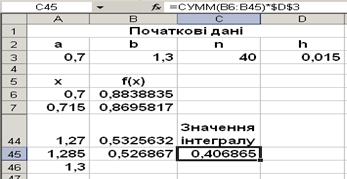
Рисунок 3.2 – Протокол рішення інтегралу за формулою прямокутників
Приклад 3.3.2Обчислити інтеграл 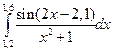 за формулою
за формулою
парабол, уточнювання провести згідно формули Річардсона.
Для вирішення задачі з’ясуємо початкові дані: a = 1,2 ; b = 1,6 , 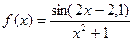 , оберемо n1 = 10 , n2 = 15 , які розмістимо на листі Excel з ім’ям „Сімпсона” . На цьому ж листі розмістимо кнопку Command Button1 , як показано на рис. 3.3 та створимо процедуру рішення.
, оберемо n1 = 10 , n2 = 15 , які розмістимо на листі Excel з ім’ям „Сімпсона” . На цьому ж листі розмістимо кнопку Command Button1 , як показано на рис. 3.3 та створимо процедуру рішення.

Рисунок 3.3 – Зразок листа Excel з ім’ям „Сімпсона”
Текст процедури:

Зразок протоколу рішення наведено на рис. 3.4 .

Рисунок 3.4 – Протокол рішення інтегралу за формулою парабол
Згідно протоколу рішення маємо:
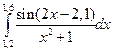 = 0б08389 .
= 0б08389 .
ЛАБОРАТОРНА РОБОТА №4
ТЕМА: Наближення (інтерполяція) функцій
4.1 Теоретичні відомості
Задача наближення функції виникає, коли для функції, даної при дискретних значеннях аргументу у вигляді таблиці (ці значення називаються вузлами інтерполяції) необхідно знайти значення функції в проміжних крапках. Накладаючи вимогу, щоб наближена функція у вузлах співпадала з табличними значеннями (рис. 4.1), одержуємо задачу інтерполяції.
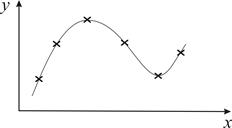
Рисунок 4.1 – Графік наближеної функції
Нехай в результаті спостережень за ходом деякого процесу побудована таблиця:
| x | x0 | x1 | x2 | … | xn |
| f(x) | f(x0) | f(x1) | f(x2) | … | f(xn) |
Тобто, функція f(x) задана таблицею значень для кінцевої безлічі значень х .
Якщо необхідно знайти значення f(x) для проміжного значення аргументу, то будують функцію φ(x) , просту для обчислень і таку, що для заданих x0 , x1 , x2 , ... , xn приймає значення f(x0) , f(x1) , f(x2) , ... , f(xn) .
В інших точках відрізка [x0, xn] вважаємо, що φ(x) приблизно визначає функцію f(x) з тим чи іншим ступенем точності.
Найчастіше, функцію φ(x) представляють у вигляді алгебраїчного багаточлена деякого ступеня.
Найпростіша інтерполяція – це лінійна, тобто, коли невідому аналітичну залежність f(x) замінюють відрізками прямих, які проходять через відповідні вузли інтерполяції. В цьому випадку потрібно визначити якому відрізку належить надане х* і за формулою лінійної інтерполяції знаходять f(x*) . Якщо xi <= x* <= xi+1 , то відповідна пряма проходить через вузли (xi , f(xі)) , (xi+1 , f(xі+1)) :
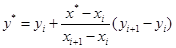 (4.1)
(4.1)
Точність підрахунків в цьому випадку незначна, тому що враховується вплив тільки 2-ох вузлів інтерполяції. Частіше будують багаточлен Pn(x) ступеня n , що в (n+1) даних точках x0 , x1 , x2 , ... , xn . приймає дані значення y0 = f(x0) , y1 = f(x
