Метод наименьших квадратов

Пусть по выборке (x_i, y_i) требуется определить оценки коэффициентов b₀ и b₁ эмпирического уравнения регрессии (5.8). В случае использования МНК минимизируется следующая функция потерь:

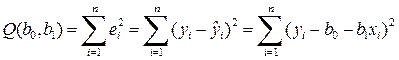. (5.10)

Нетрудно заметить, что функция Q является квадратичной функцией двух параметров b₀ и b₁, поскольку x_i и y_i – известные данные наблюдений. Поскольку функция Q непрерывна, выпукла и ограничена снизу (Q³0), то она имеет минимум.

Необходимым условием существования минимума функции двух переменных (5.10) является равенство нулю ее частных производных по неизвестным параметрам b₀ и b₁:

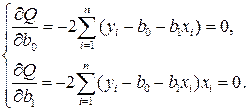(5.11)

После преобразований получим систему нормальных уравнений (систему линейных алгебраических уравнений) для определения параметров простой линейной регрессии:

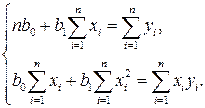(5.12)

Разделив оба уравнения на n, получим:

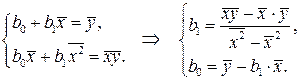(5.13)

Здесь 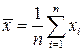, , 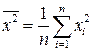, 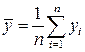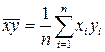. Таким образом, оценки параметров простой линейной регрессии по МНК определяются по формулам (5.13).

Нетрудно заметить, что b₁ можно вычислить по формуле

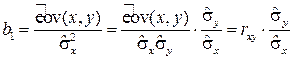, (5.14)

где r_xy – выборочный коэффициент корреляци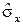и, и 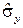– средние квадратичные отклонения. Таким образом, коэффициент регрессии b₁ пропорционален коэффициенту корреляции. Следовательно, если коэффициент корреляции r_xy уже рассчитан, то легко может быть найден коэффициент регрессии b₁ по формуле (5.14).

Отметим, что кроме уравнения регрессии Y на X: 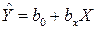, для тех же эмпирических данных может быть найдено уравнение регрессии X на Y: 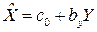. Коэффициенты регрессии b_x и b_y в этом случае будут связаны равенством:

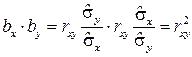. (5.15)

Подставляя значения b₀ и b₁, вычисленные по формулам (5.13), в (5.8), получим уравнение линейной регрессии Y на X:

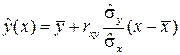. (5.16)

Аналогично можно получить уравнение линейной регрессии X на Y:

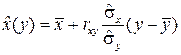. (5.17)

Можно заметить, что обе прямые регрессии пересекаются в точке 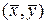. Причем, чем больше коэффициент корреляции, тем меньше угол j между прямыми (рис. 5.2). В частности, если r=±1, то обе прямые регрессии совпадут. Если коэффициент корреляции равен нулю, то линии регрессии будут параллельны координатным осям.

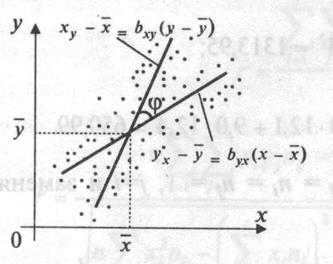
Рис. 5.2

Полученные формулы для коэффициентов регрессии позволяют сделать ряд выводов:

1. Эмпирическая прямая регрессии обязательно проходит через точку .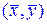

2. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений 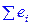, а также среднее значение отклонений 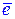равны нулю.

% Действительно, из формулы 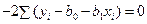в соотношении (5.11) следует, что . &

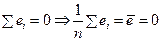3. Случайные отклонения e_i не коррелированы с наблюдаемыми значениями y_i зависимой переменной Y.

% Для обоснования данного утверждения покажем, что ковариация между Y и e равна нулю. Действительно,

.

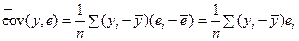Покажем, что 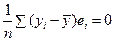. Просуммировав по i все соотношения (5.9), получим:

,

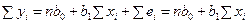т.к. 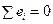. Разделив последнее соотношение на n, получим 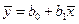. Вычитая из (5.9) полученное соотношение, приходим к следующей формуле:

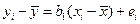. (5.18)

Тогда

.

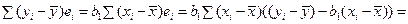
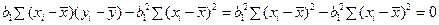Следовательно, . &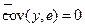

4. Случайные отклонения e_i не коррелированы с наблюдаемыми значениями x_i независимой переменной X.

% Действительно, 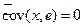в силу второй формулы системы (5.11). &

Для иллюстрации МНК рассмотрим следующий пример,

Пример 5.1. Для анализа зависимости объема потребления домохозяйства Y (у.е) от располагаемого дохода X (у.е) отобрана выборка объема n=12 (помесячно в течение месяца, результаты которой приведены в таблице 5.1. Необходимо определить вид зависимости; по МНК оценить параметры уравнения регрессии Y на X; оценить силу линейной зависимости между Y на X; спрогнозировать потребление при доходе X=160.

Табл. 5.1

i

xi

yi

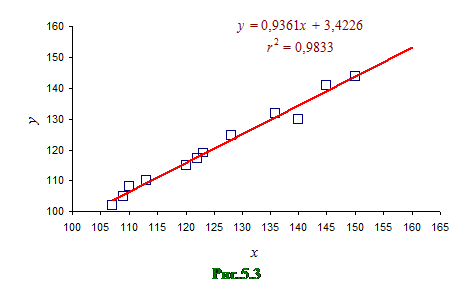
Решение. Для определения вида регрессионной зависимости построим корреляционное поле (рис.5.3). По расположению точек на корреляционном поле полагаем, что зависимость между X и Y линейная: 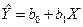. Для расчетов по МНК составим расчетную таблицу (табл. 5.2):

Табл. 5.2

i	xi	yi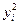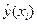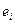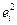
						103,5832	-1,5832	2,5065
						105,4554	-0,4554	0,2074
						106,3914	1,6086	2,5875
						109,1997	0,8003	0,6405
						115,7522	-0,7522	0,5659
						117,6244	-0,6244	0,3899
						118,5605	0,4395	0,1932
						123,2409	1,7591	3,0945
						130,7295	1,2705	1,6141
						134,4739	-4,4739	20,0153
						139,1543	1,8457	3,4068
						143,8347	0,1653	0,0273
Сумма						-	0,0000	35,2488
Среднее	125,25	120,6667	15884,75	15298,08	14736,17	-	-	-

Согласно МНК, по формулам (5.13) вычисляем

;

.

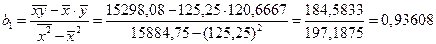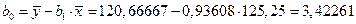Таким образом, уравнение парной линейной регрессии имеет вид:

.

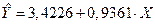Изобразим данную прямую регрессии на корреляционном поле (рис.5.3). По этому уравнению рассчитаем 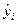, а также .

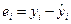Для анализа силы линейной зависимости вычислим коэффициент корреляции. Для этого предварительно найдем средние квадратичные отклонения:

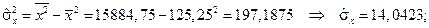
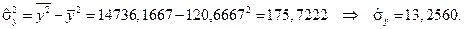
Тогда

.

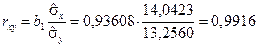Данное значение коэффициента корреляции позволяет сделать вывод об очень сильной (близкой к функциональной) линейной зависимости между рассматриваемыми переменными X и Y. Это также подтверждается расположением точек на корреляционном поле.

Прогнозируемое потребление при располагаемом доходе x=160 для данной модели составит .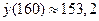

Построенное уравнение регрессии в любом случае требует определенной интерпретации и анализа. Интерпретация требует словесного описания полученных результатов с трактовкой найденных коэффициентов, с тем чтобы построенная зависимость стала понятной человеку, не являющимся специалистом в эконометрическом анализе. Коэффициент b₁ показывает, на какую величину изменится Y, если X возрастет на одну единицу. В случае примера 5.1 он может трактоваться как предельная склонность к потреблению, т.е. он показывает, что объем потребления изменится на 0,9361, если располагаемый доход возрастает на одну единицу.

Свободный член b₀ уравнения регрессии определяет прогнозируемое значение Y при величине X, равной нулю. Однако здесь необходима определенная осторожность. Очень важно, насколько далеко данные наблюдений за объясняющей переменной отстоят на оси ординат (зависимой переменной), т.к. даже при удачном подборе уравнения регрессии для интервала наблюдений нет гарантии, что оно останется таковым и вдали от выборки. В случае примера 5.1 значение b₀=3,4226 говорит о том, что при нулевом располагаемом доходе расходы на потребление составят в среднем 3,4226 у.е. Этот факт можно объяснить для отдельного домохозяйства (оно может тратить накопленные или одолженные средства), но для совокупности домохозяйств он теряет смысл. В любом случае значение коэффициента b₀ определяет точку пересечения прямой регрессии с осью ординат и характеризует сдвиг линии регрессии вдоль оси Y. â

Следует помнить, что эмпирические коэффициенты регрессии b₀ и b₁ являются лишь оценками теоретических коэффициентов b₀ и b₁, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных. Индивидуальные значения переменных могут отклоняться от модельных значений. В нашем примере эти отклонения выражены через значения e_i, которые являются оценками отклонений e_i для генеральной совокупности. Однако при определенных условиях уравнение регрессии служит незаменимым и очень качественным инструментом. Обсуждение этих условий будет проведено в дальнейшем.

5.1.5. Условия Гаусса-Маркова. Классическая линейная
регрессионная модель

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Однако они являются лишь оценками. Поэтому возникает вопрос о том, насколько они надежны, насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности, насколько близки оценки b₀ и b₁ коэффициентов регрессии к своим теоретическим прототипам b₀ и b₁, как близко оцененное значение 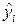к условному математическому ожиданию 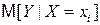. Для ответа на эти вопросы необходимы определенные дополнительные исследования.

Как следует из равенства (5.6), значения y_i зависят от значений x_i и случайных отклонений e_i. Следовательно, переменная Y является случайной величиной, напрямую связанной с e_i. Можно показать, что оценки коэффициентов регрессии – случайные величины, также зависящие от случайного отклонения.

Рассмотрим модель простой линейной регрессии

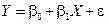. (5.19)

Пусть на основе выборки из n наблюдений оценивается регрессия:

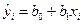. (5.20)

Будем также полагать, что X – это не случайная экзогенная переменная. Иными словами, ее значения во всех наблюдениях можно считать заранее заданными и никак не связанными с исследуемой зависимостью.

В соответствии с формулой (5.14)

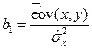. (5.21)

Это означает, что коэффициент b₁ также является случайной величиной. Теоретически коэффициент b₁ можно разложить на неслучайную и случайную составляющие.

.

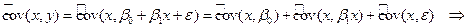
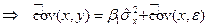Здесь использованы следующие правила вычисления ковариации:

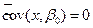, так как ; .

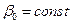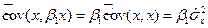Следовательно,

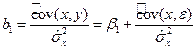. (5.22)

Аналогичный результат можно получить и для коэффициента b₀. Учитывая, что

.

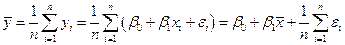В результате получим

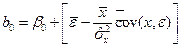. (5.23)

Таким образом, коэффициенты регрессии b₁ и b₀, полученные по любой выборке, представляется в виде суммы двух слагаемых: 1) постоянной величины, равной истинному значению коэффициента; 2) случайной составляющей, зависящей от случайного фактора e.

Отметим, что на практике такое разложение осуществить невозможно, поскольку неизвестны истинные значения b₀ и b₁, а также значения отклонений для всей генеральной совокупности. Они интересуют нас потому, что при определенных предположениях позволяют получить некоторую информацию о теоретических свойствах b₀ и b₁.

Итак, мы видим, что свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей e. Это означает, что до тех пор, пока не будет определенности о вероятностном поведении e, мы не можем ничего сказать о статистических свойствах этих оценок.

Для того чтобы регрессионный анализ, основанный на обычном МНК, давал наилучшие из всех возможных результаты, случайное отклонение e должно удовлетворять определенным условиям, которые известны как условия Гаусса-Маркова.

1⁰. Математическое ожидание случайного отклонения e_i равно нулю: 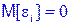для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайное отклонение может быть либо положительным, либо отрицательным, но оно не должно иметь систематического смещения. Фактически если уравнение регрессии включает постоянное слагаемое b₀, то это условие практически выполняется автоматически; если постоянное слагаемое b₀ отсутствует, то это условие может и не выполняться.

2⁰. Дисперсия случайных отклонений e_i постоянна: 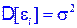для всех наблюдений.

Данное условие подразумевает, что несмотря на то, при каждом конкретном наблюдении случайное отклонение может больше или меньше, не должно быть некой априорной причины, которая вызывает большую ошибку в одних наблюдениях, чем в других. Постоянная дисперсия обычно обозначается 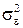или, более кратко, 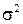. Величина 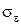, конечно, неизвестна. Одна из задач регрессионного анализа состоит в оценке этой величины.

Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному МНК, будут не эффективными, и можно получить более надежные результаты путем применения модифицированного МНК.

3⁰. Случайные отклонения e_i и e_j являются коррелированными: 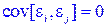для i¹j.

Это условие предполагает отсутствие систематической связи между значениями случайного отклонения в любых двух наблюдениях. Например, если случайное отклонение велико и положительно в одном наблюдении, то это не должно обуславливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении. Отметим, что с учетом выполнимости условия 1⁰, данное условие можно переписать в виде: 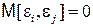(i¹j).

Если это условие не выполняется, то регрессия, оцененная по обычному МНК, вновь даст не эффективные результаты. Более надежные результаты можно получить также при помощи применения модифицированного МНК.

При выполнении условий 1⁰-3⁰ модель (5.19) называется классической линейной регрессионной моделью.

Наряду с выполнимостью указанных условий при построении регрессионных моделей делаются еще некоторые предположения.

4⁰. Объясняющая переменная x_i есть величина неслучайная

Если это условие не выполняется, то оценки коэффициентов регрессии могут оказаться смещенными и несостоятельными. Нарушение этого условия может быть связано с ошибками измерения объясняющих переменных или с использованием лаговых переменных.

В регрессионном анализе часто вместо условия о неслучайности объясняющей переменной используется более слабое условие о независимости (некоррелированности) распределений случайного отклонения и объясняющей переменной. Данное условие предполагает выполнение следующего условия

.

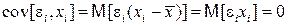Следовательно, данное условие можно записать в виде 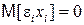. Обычно это условие выполняется автоматически, если объясняющие переменные не являются случайными в данной модели. Получаемые при этом оценки коэффициентов регрессии обладают теми же свойствами, что и оценки, полученные при использовании условия о неслучайности объясняющей переменной.

Отметим, что выполнимость данного условия не столь критичны для эконометрических моделей. В дальнейшем мы рассмотрим некоторые случаи, в которых данное условие нарушается и последствия этого.

5⁰. Случайное отклонение имеет нормальное распределение: .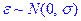

Дело в том, что если случайное отклонение имеет нормальное распределение, то такое же распределение будут иметь и коэффициенты регрессии. Это условие удобно для проведения проверки гипотез и построения доверительных интервалов. Предположение о нормальности основывается на центральной предельной теореме, в соответствие с которой, если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, т она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения. Случайное отклонение e определяется многими факторами, которые не входят в явной форме в уравнение регрессии. Поэтому даже если мы не знаем о распределении этих факторов, у нас есть все основания предположить, что оно нормально распределено. В большинстве случаев это не приводит к большим проблемам.

При выполнении условий 1⁰-5⁰ модель (5.19) называется нормальной классической линейной регрессионной моделью (НКЛРМ).