Рассмотрим граф 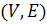 и рассмотрим множество цветов на числах
и рассмотрим множество цветов на числах 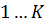 .
.
Определение. Правильной раскраской графа называется задание каждой вершине некоторого цвета, такого, что любая пара смежных вершин раскрашена в разные цвета.
Определение. Минимальное число красок, которое необходимо для окраски графа называется хроматическим числом графа.
Пример. Полный граф на 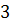 вершинах имеет хроматическое число
вершинах имеет хроматическое число 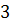 .
.
Любой полный граф на 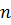 вершинах имеет хроматическое число
вершинах имеет хроматическое число 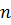 . Действительно, приписав к каждой вершине свой цвет, получится правильная раскраска графа. Если число цветов
. Действительно, приписав к каждой вершине свой цвет, получится правильная раскраска графа. Если число цветов 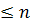 , то какая-то пара вершин будет окрашена в один и тот же цвет. Но в полном графе присутствуют все ребра. Поэтому это будет неправильная раскраска.
, то какая-то пара вершин будет окрашена в один и тот же цвет. Но в полном графе присутствуют все ребра. Поэтому это будет неправильная раскраска.
Утверждение. Каждый планарный граф можно раскрасить не более чем 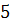 красками, т.е. хроматическое число планарного графа
красками, т.е. хроматическое число планарного графа 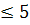 .
.
Будем считать, что рассматриваемый планарный граф является связным. В противном случае достаточно рассмотреть связные компоненты графа.
Предварительное утверждение: покажем, что в каждом планарном графе существует вершина, степень которой 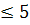 (степень вершины – число ребер графа, один из концов которых является данной вершиной).
(степень вершины – число ребер графа, один из концов которых является данной вершиной).
Доказательство:
Если число вершин в рассматриваемом графе 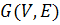 не больше
не больше 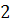 (
( 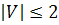 ), то утверждение очевидно. Поэтому будем считать, что число вершин в рассматриваемом графе не меньше
), то утверждение очевидно. Поэтому будем считать, что число вершин в рассматриваемом графе не меньше 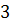 (
( 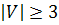 ). Будем считать, что граф связный. Рассмотрим какую-либо планарную укладку рассматриваемого графа.
). Будем считать, что граф связный. Рассмотрим какую-либо планарную укладку рассматриваемого графа.
Число вершин в графе будем обозначать 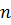 (
( 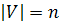 ). Число ребер в графе обозначим
). Число ребер в графе обозначим 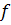 (
( 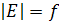 ). Число граней графа обозначим
). Число граней графа обозначим 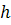 (
( 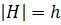 ).
).
Введем следующие обозначения: 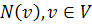 – степень вершины
– степень вершины 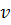 ,
, 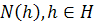 – число ребер, возникающих при обходе грани
– число ребер, возникающих при обходе грани 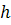 по ее периметру. Например,
по ее периметру. Например, 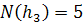 .
.
Рассмотрим следующую сумму:
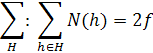
Доказательство:
Действительно, каждое ребро при обходе по всем граням будет учитываться дважды. Если это ребро является границей 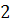 различных граней, то для каждой из
различных граней, то для каждой из 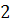 граней ребро будет учитываться по одному разу, как ребро
граней ребро будет учитываться по одному разу, как ребро 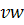 .
.
Если же ребро входит в древесную часть какой либо из граней, как висячее ребро на рисунке, то это ребро будет пройдено по периметру данной грани дважды.
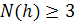 (по крайней мере
(по крайней мере 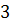 ребра нужно, чтобы окружить некоторую грань). Число граней будем обозначать
ребра нужно, чтобы окружить некоторую грань). Число граней будем обозначать 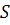 (
( 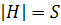 ). Получим:
). Получим:
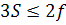 | (*) |
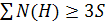 . Применим формулу Эйлера для планарного связного графа.
. Применим формулу Эйлера для планарного связного графа.
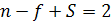
Тогда 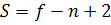 . Подставим данное значение в (*):
. Подставим данное значение в (*):
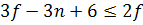
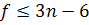 | (**) |
Покажем справедливость следующего равенства:
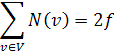
Действительно, в сумме слева каждое ребро учитывается дважды: как ребро, смежное двум своим концам. Предположим противное: степень каждой вершины 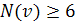 . Получим следующее неравенство:
. Получим следующее неравенство:
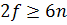
Оно противоречит неравенству
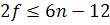
(**). Что и требовалось доказать.
Доказательство основного утверждения (хроматическое число планарного графа 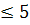 ):
):
Доказательство проводится по индукции по числу вершин в планарном графе. Для графа с одной вершиной утверждение очевидно. Допустим, что утверждение доказано для любого планарного графа с числом вершин 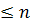 . Рассмотрим планарный граф
. Рассмотрим планарный граф 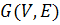 с числом вершин
с числом вершин 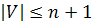 . В планарном графе обязательно найдется вершина со степенью
. В планарном графе обязательно найдется вершина со степенью 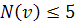 . Обозначим эту вершину
. Обозначим эту вершину 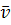 и рассмотрим какую-либо планарную укладку графа.
и рассмотрим какую-либо планарную укладку графа.
Если 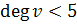 , то удаляем вершину и ребра инцидентные ей и поулчаем планарный граф с
, то удаляем вершину и ребра инцидентные ей и поулчаем планарный граф с 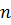 вершинами. По предположению индукции, такой граф можно раскрасить
вершинами. По предположению индукции, такой граф можно раскрасить 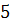 красками. Тогда вершину
красками. Тогда вершину 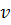 закрасим незадействованной краской , т.к. число смежных вершин с
закрасим незадействованной краской , т.к. число смежных вершин с 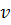
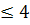 . Поэтому будем предполагать, что
. Поэтому будем предполагать, что 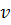 смежна с
смежна с 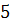 вершинами. Обозначим вершины, смежные с ней:
вершинами. Обозначим вершины, смежные с ней: 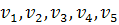 . Удалим вершину
. Удалим вершину 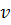 и инцидентные ей ребра. В результате получим планарный граф
и инцидентные ей ребра. В результате получим планарный граф 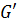 с
с 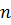 вершинами.
вершинами.
По предположению индукции, такой граф можно окрасить 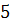 красками. Будем считать, что вершины
красками. Будем считать, что вершины 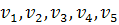 окрашены в цвета
окрашены в цвета 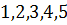 соответственно (если какой-либо цвет отсутствует, то вершину окрашиваем в незадействованный цвет). Рассмотрим граф
соответственно (если какой-либо цвет отсутствует, то вершину окрашиваем в незадействованный цвет). Рассмотрим граф 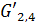 – подграф
– подграф 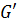 , который порожден вершинами, окрашенными в цвета
, который порожден вершинами, окрашенными в цвета 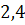 (т.е. подграф с вершинами, окрашенными в цвета
(т.е. подграф с вершинами, окрашенными в цвета 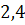 и всеми ребрами, оба конца которых принадлежат рассматриваемому множеству вершин).
и всеми ребрами, оба конца которых принадлежат рассматриваемому множеству вершин).
Если вершины 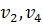 находятся в различных компонентах связности данного подграфа, то поменяем цвета (
находятся в различных компонентах связности данного подграфа, то поменяем цвета ( 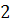 на
на 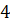 ) в той компоненте связности, которой принадлежит вершина
) в той компоненте связности, которой принадлежит вершина 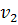 . В результате получим правильную окраску. При этом вершина
. В результате получим правильную окраску. При этом вершина 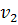 будет окрашена в
будет окрашена в 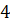 цвет. Тогда вершину
цвет. Тогда вершину 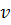 в первоначальном графе
в первоначальном графе 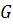 можно окрасить в освободившийся
можно окрасить в освободившийся 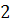 цвет. Поэтому будем считать, что
цвет. Поэтому будем считать, что 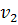 и
и 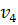 находятся в одной компоненте связности подграфа
находятся в одной компоненте связности подграфа 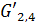 . Следовательно, существует цепь из вершин, которые окрашены в цвета
. Следовательно, существует цепь из вершин, которые окрашены в цвета 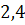 .
.
Рассмотрим аналогичный подграф 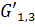 , который порожден вершинами, окрашенными в цвета 1,3. При этом вершины
, который порожден вершинами, окрашенными в цвета 1,3. При этом вершины 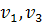 находятся в различных компонентах связности –так как вершина
находятся в различных компонентах связности –так как вершина 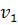 окружена циклом, состоящем из вершин, окрашенных в цвета
окружена циклом, состоящем из вершин, окрашенных в цвета 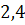 , а вершина
, а вершина 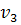 находится вне цикла. Рассмотрим компоненту связности, которой принадлежит вершина
находится вне цикла. Рассмотрим компоненту связности, которой принадлежит вершина 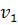 . Поменяем в данной компоненте цвет 1 на 3, а 3 на
. Поменяем в данной компоненте цвет 1 на 3, а 3 на 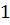 . Получаем правильную окраску
. Получаем правильную окраску 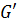 , в которой вершина
, в которой вершина 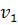 окрашена в 3 цвет. Тогда вершину
окрашена в 3 цвет. Тогда вершину 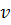 окрасим в 1 цвет.
окрасим в 1 цвет.
Что и требовалось доказать.
Утверждение. Хроматическое число любого планарного графа не превышает 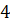 .
.
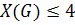
Утверждение. Любой граф можно уложить в 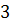 -х мерном пространстве без пересечения ребер.
-х мерном пространстве без пересечения ребер.
Доказательство.
Рассмотрим прямолинейный отрезок и расположенные на нем вершины графа  . Для каждого ребра отведем плоскость.
. Для каждого ребра отведем плоскость. 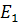 для
для 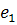 ,
, 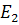 для
для 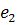 и т.д. расположим эти плоскости в книгу, как изображено на рисунке. Каждое ребро графа расположено в соответствующей ему плоскости. Так как ребра проведены через различные плоскости, то они не пересекаются.
и т.д. расположим эти плоскости в книгу, как изображено на рисунке. Каждое ребро графа расположено в соответствующей ему плоскости. Так как ребра проведены через различные плоскости, то они не пересекаются.
Что и требовалось доказать
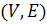 и рассмотрим множество цветов на числах
и рассмотрим множество цветов на числах 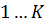 .
.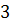 вершинах имеет хроматическое число
вершинах имеет хроматическое число 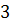 .
.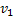
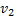
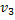
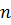 вершинах имеет хроматическое число
вершинах имеет хроматическое число 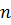 . Действительно, приписав к каждой вершине свой цвет, получится правильная раскраска графа. Если число цветов
. Действительно, приписав к каждой вершине свой цвет, получится правильная раскраска графа. Если число цветов 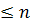 , то какая-то пара вершин будет окрашена в один и тот же цвет. Но в полном графе присутствуют все ребра. Поэтому это будет неправильная раскраска.
, то какая-то пара вершин будет окрашена в один и тот же цвет. Но в полном графе присутствуют все ребра. Поэтому это будет неправильная раскраска.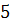 красками, т.е. хроматическое число планарного графа
красками, т.е. хроматическое число планарного графа 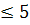 .
.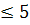 (степень вершины – число ребер графа, один из концов которых является данной вершиной).
(степень вершины – число ребер графа, один из концов которых является данной вершиной).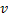
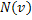
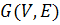 не больше
не больше 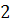 (
( 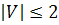 ), то утверждение очевидно. Поэтому будем считать, что число вершин в рассматриваемом графе не меньше
), то утверждение очевидно. Поэтому будем считать, что число вершин в рассматриваемом графе не меньше 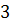 (
( 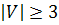 ). Будем считать, что граф связный. Рассмотрим какую-либо планарную укладку рассматриваемого графа.
). Будем считать, что граф связный. Рассмотрим какую-либо планарную укладку рассматриваемого графа.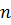 (
( 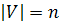 ). Число ребер в графе обозначим
). Число ребер в графе обозначим 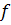 (
( 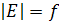 ). Число граней графа обозначим
). Число граней графа обозначим 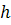 (
( 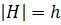 ).
).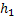
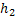
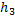
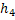
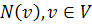 – степень вершины
– степень вершины 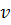 ,
, 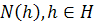 – число ребер, возникающих при обходе грани
– число ребер, возникающих при обходе грани 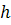 по ее периметру. Например,
по ее периметру. Например, 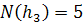 .
.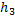
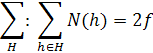
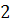 различных граней, то для каждой из
различных граней, то для каждой из 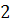 граней ребро будет учитываться по одному разу, как ребро
граней ребро будет учитываться по одному разу, как ребро 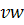 .
.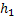
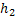
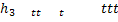
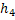
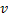
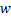
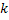
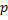
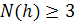 (по крайней мере
(по крайней мере 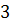 ребра нужно, чтобы окружить некоторую грань). Число граней будем обозначать
ребра нужно, чтобы окружить некоторую грань). Число граней будем обозначать 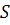 (
( 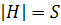 ). Получим:
). Получим: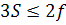
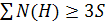 . Применим формулу Эйлера для планарного связного графа.
. Применим формулу Эйлера для планарного связного графа.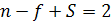
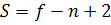 . Подставим данное значение в (*):
. Подставим данное значение в (*):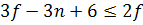
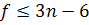
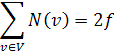
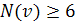 . Получим следующее неравенство:
. Получим следующее неравенство: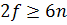
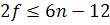
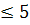 ):
):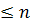 . Рассмотрим планарный граф
. Рассмотрим планарный граф 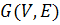 с числом вершин
с числом вершин 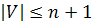 . В планарном графе обязательно найдется вершина со степенью
. В планарном графе обязательно найдется вершина со степенью 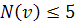 . Обозначим эту вершину
. Обозначим эту вершину 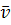 и рассмотрим какую-либо планарную укладку графа.
и рассмотрим какую-либо планарную укладку графа.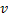
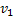
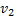
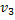
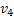
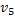
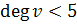 , то удаляем вершину и ребра инцидентные ей и поулчаем планарный граф с
, то удаляем вершину и ребра инцидентные ей и поулчаем планарный граф с 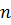 вершинами. По предположению индукции, такой граф можно раскрасить
вершинами. По предположению индукции, такой граф можно раскрасить 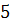 красками. Тогда вершину
красками. Тогда вершину 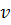 закрасим незадействованной краской , т.к. число смежных вершин с
закрасим незадействованной краской , т.к. число смежных вершин с 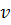
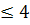 . Поэтому будем предполагать, что
. Поэтому будем предполагать, что 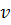 смежна с
смежна с 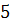 вершинами. Обозначим вершины, смежные с ней:
вершинами. Обозначим вершины, смежные с ней: 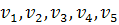 . Удалим вершину
. Удалим вершину 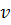 и инцидентные ей ребра. В результате получим планарный граф
и инцидентные ей ребра. В результате получим планарный граф 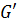 с
с 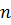 вершинами.
вершинами.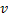
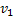
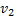
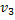
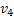
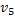
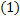
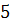 красками. Будем считать, что вершины
красками. Будем считать, что вершины 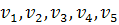 окрашены в цвета
окрашены в цвета 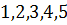 соответственно (если какой-либо цвет отсутствует, то вершину окрашиваем в незадействованный цвет). Рассмотрим граф
соответственно (если какой-либо цвет отсутствует, то вершину окрашиваем в незадействованный цвет). Рассмотрим граф 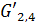 – подграф
– подграф 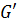 , который порожден вершинами, окрашенными в цвета
, который порожден вершинами, окрашенными в цвета 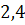 (т.е. подграф с вершинами, окрашенными в цвета
(т.е. подграф с вершинами, окрашенными в цвета 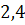 и всеми ребрами, оба конца которых принадлежат рассматриваемому множеству вершин).
и всеми ребрами, оба конца которых принадлежат рассматриваемому множеству вершин).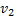
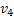
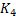
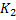
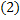
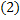
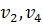 находятся в различных компонентах связности данного подграфа, то поменяем цвета (
находятся в различных компонентах связности данного подграфа, то поменяем цвета ( 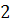 на
на 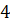 ) в той компоненте связности, которой принадлежит вершина
) в той компоненте связности, которой принадлежит вершина 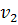 . В результате получим правильную окраску. При этом вершина
. В результате получим правильную окраску. При этом вершина 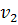 будет окрашена в
будет окрашена в 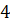 цвет. Тогда вершину
цвет. Тогда вершину 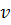 в первоначальном графе
в первоначальном графе 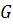 можно окрасить в освободившийся
можно окрасить в освободившийся 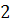 цвет. Поэтому будем считать, что
цвет. Поэтому будем считать, что 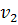 и
и 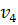 находятся в одной компоненте связности подграфа
находятся в одной компоненте связности подграфа 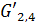 . Следовательно, существует цепь из вершин, которые окрашены в цвета
. Следовательно, существует цепь из вершин, которые окрашены в цвета 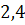 .
.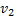
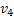
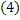
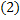
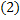
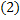
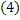
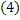
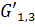 , который порожден вершинами, окрашенными в цвета 1,3. При этом вершины
, который порожден вершинами, окрашенными в цвета 1,3. При этом вершины 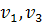 находятся в различных компонентах связности –так как вершина
находятся в различных компонентах связности –так как вершина 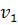 окружена циклом, состоящем из вершин, окрашенных в цвета
окружена циклом, состоящем из вершин, окрашенных в цвета 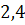 , а вершина
, а вершина 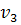 находится вне цикла. Рассмотрим компоненту связности, которой принадлежит вершина
находится вне цикла. Рассмотрим компоненту связности, которой принадлежит вершина 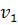 . Поменяем в данной компоненте цвет 1 на 3, а 3 на
. Поменяем в данной компоненте цвет 1 на 3, а 3 на 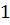 . Получаем правильную окраску
. Получаем правильную окраску 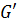 , в которой вершина
, в которой вершина 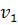 окрашена в 3 цвет. Тогда вершину
окрашена в 3 цвет. Тогда вершину 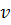 окрасим в 1 цвет.
окрасим в 1 цвет. .
.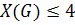
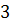 -х мерном пространстве без пересечения ребер.
-х мерном пространстве без пересечения ребер.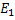
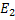
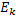
 . Для каждого ребра отведем плоскость.
. Для каждого ребра отведем плоскость. 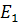 для
для 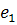 ,
, 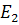 для
для 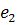 и т.д. расположим эти плоскости в книгу, как изображено на рисунке. Каждое ребро графа расположено в соответствующей ему плоскости. Так как ребра проведены через различные плоскости, то они не пересекаются.
и т.д. расположим эти плоскости в книгу, как изображено на рисунке. Каждое ребро графа расположено в соответствующей ему плоскости. Так как ребра проведены через различные плоскости, то они не пересекаются.