Нормальный закон распределения. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Функция Лапласа
По определению плотность нормально распределенной случайной величины равна
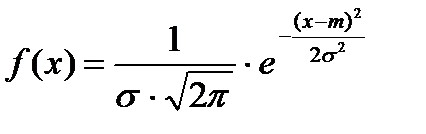
Возможные значения такой величины Х могут принимать любые действительные значения -∞<Х<∞, а распределение зависит от двух параметров . -∞<m<∞ и -∞<σ<∞.
Таким образом, график функции f(х) будет таким:
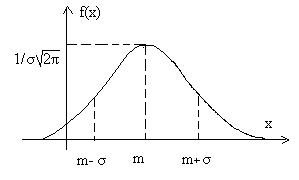 При изменении m кривая f(x) скользит вдоль оси абсцисс, не меняя своей формы. При изменении σ кривая меняет свою форму: если σ увеличивается, то кривая становится ниже и шире и наоборот.
При изменении m кривая f(x) скользит вдоль оси абсцисс, не меняя своей формы. При изменении σ кривая меняет свою форму: если σ увеличивается, то кривая становится ниже и шире и наоборот.
Если m=0 и σ=1, то закон нормального распределения называется стандартным. В этом случае
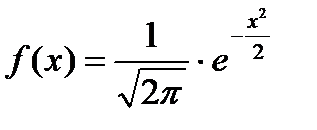
Если случайная величина Храспределена по нормальному закону с параметрами m и σ , то этот факт записывают так:. 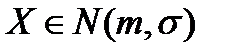
Вычислим математическое ожидание случайной величины
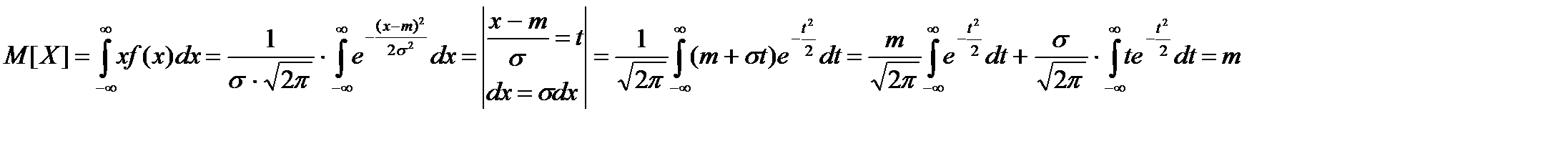
Таким образом, параметр m - это математическое ожидание случайной величины X.
Вычислим теперь дисперсию
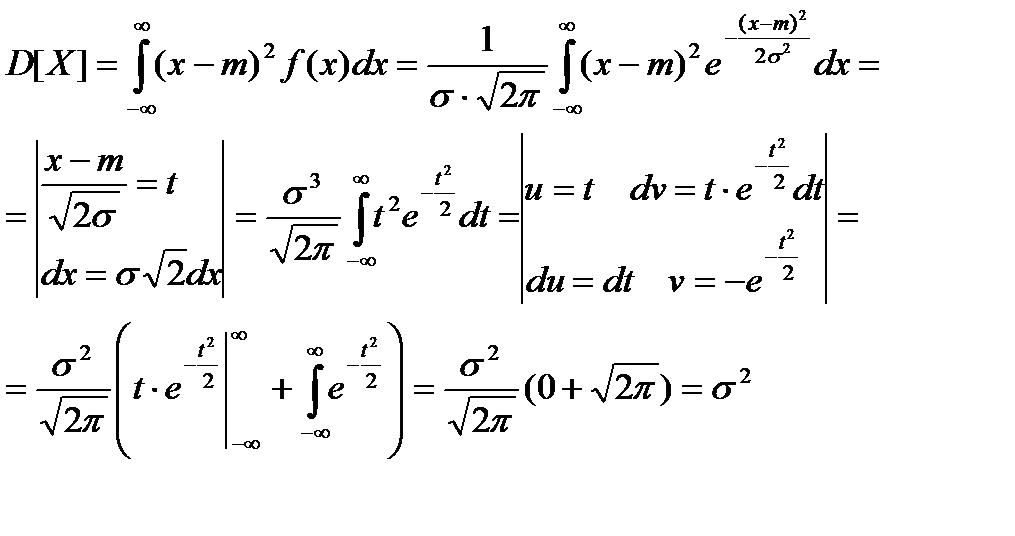
где мы использовали то, что по правилу Лопиталя
Таким образом, параметр σ - это среднеквадратическое отклонение, поскольку σ2- это дисперсия.
Мода и медиана нормального распределения совпадает с математическим ожиданием, т.к. максимум f(x) достигается при x=m и
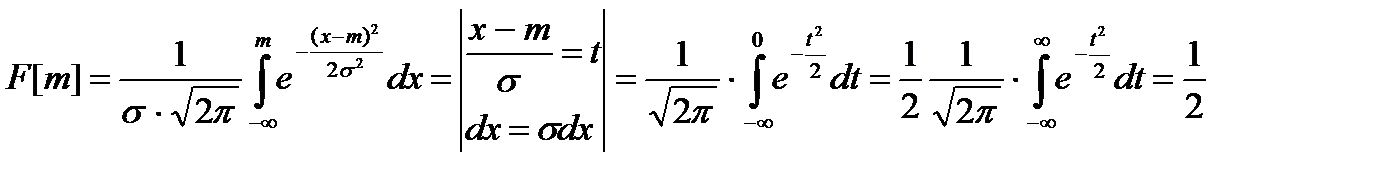
 где
где
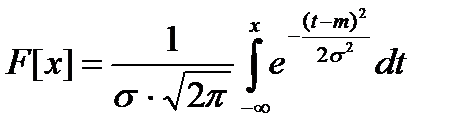
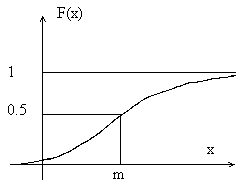
функция распределения закона 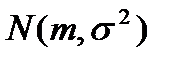 которая имеет график, представленный на рисунке.
которая имеет график, представленный на рисунке.
Пусть 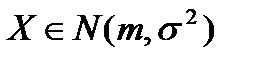 Вычислим Р(а<Х<b) - вероятность попадания нормально распределенной случайной величины в заданный интервал. По свойству плотности распределения имеем
Вычислим Р(а<Х<b) - вероятность попадания нормально распределенной случайной величины в заданный интервал. По свойству плотности распределения имеем
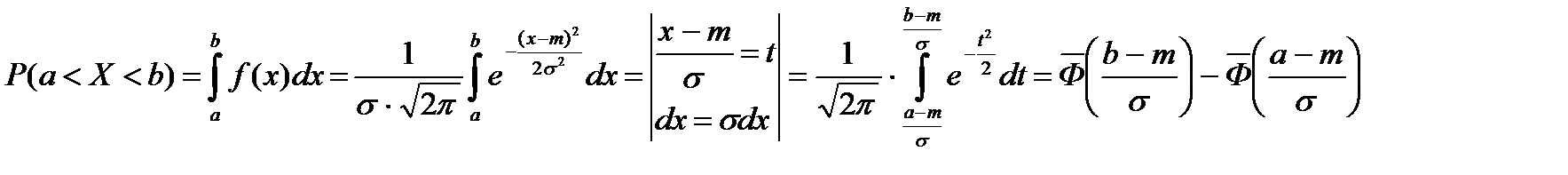
где мы использовали формулу Ньютона-Лейбница для определенных интегралов, а 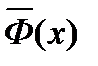 - любая первообразная для подынтегральной функции
- любая первообразная для подынтегральной функции
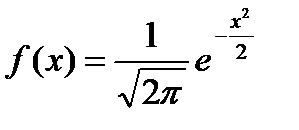
Любая первообразная может быть рассчитана по формуле
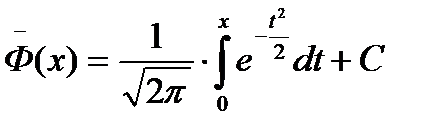
где С- произвольная постоянная. Это можно легко проверить дифференцированием .
При С=0 мы получаем функцию Лапласа
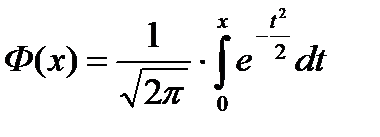
а при С=∞ -функцию распределения стандартного нормального закона
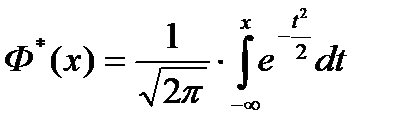
Нетрудно получить связь между Ф*(х) и Ф(х).
Окончательно получаем
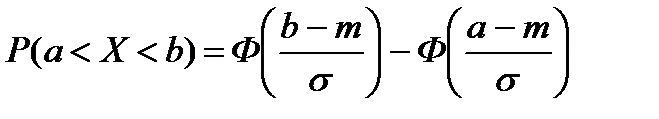
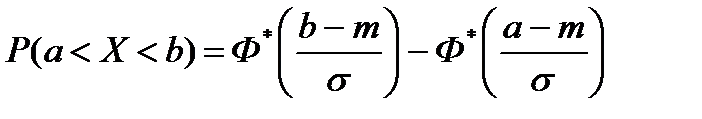
В зависимости от имеющихся у нас под руками таблиц мы воспользуемся той или иной формулой. Отметим, что пользоваться таблицами функции Лапласа удобней, так как она нечетна и мы легко - находим ее значения при отрицательном аргументе (обычно, таблицы заданы только для положительных значений аргумента). Пользоваться таблицами функции Ф*(х) в этом случае несколько неудобнее, если она задана только для положительных значений аргумента.
ПРИМЕР 1. Пусть 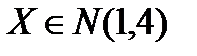 Найдем вероятность того, что Х примет значение из интервала ]0;3[.
Найдем вероятность того, что Х примет значение из интервала ]0;3[.
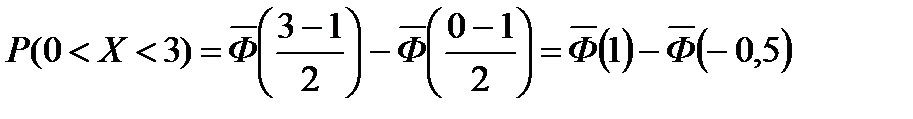
По таблице функции Лапласа получаем
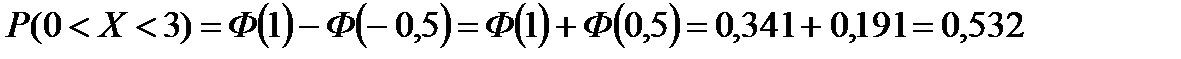
По таблице функции распределения стандартного нормального закона получаем, используя ее связь с функцией Лапласа:
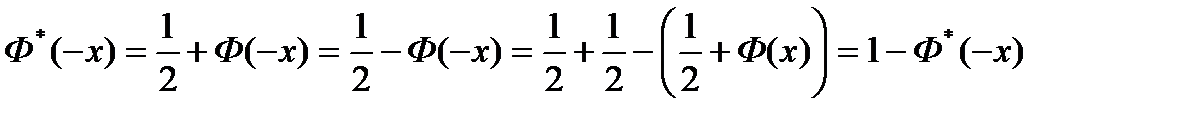
 В этом примере мы вывели полезную формулу
В этом примере мы вывели полезную формулу
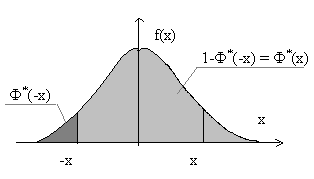
Ф*(-х)=1-Ф*(х),
которую легко пояснить следующим рисунком.
Найдем вероятность попадания нормальной случайной величины в интервал ]m-l,m+l[, симметричный относительно математического ожидания:
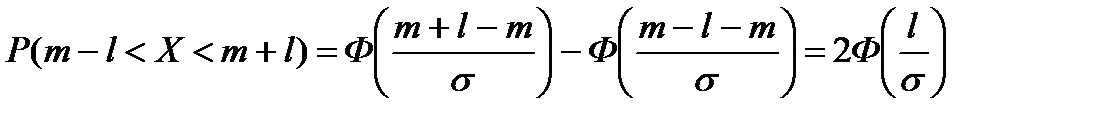
При различных l получаем
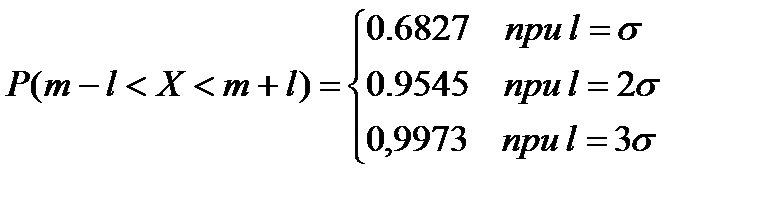
Как мы видим, хотя теоретически возможные значения Х могут быть любые, но практически все значения попадают в интервал ]m-3σ,m+3σ[. Этот факт обычно называют правилом «трех сигм». При нормальном распределении из 10000 измерений только 27 имеют «законное» право выйти из этого интервала ( событие маловероятное и им обычно пренебрегают). Поэтому можно считать, что все возможные значения нормальной случайной величины находятся в этом интервале.
