Глава 1 Гармонические колебания
КОЛЕБАНИЯ И ВОЛНЫ
Рекомендовано к изданию Ученым советом федерального государственного бюджетного образовательного учреждения высшего профессионального образования ²Оренбургский государственный университет² в качестве учебного пособия для студентов, обучающихся по программам высшего профессионального образования инженерно-технических направлений подготовки
Оренбург
УДК 534 (07)
ББК 22.336 я 7
П 27
Рецензент - доктор физико-математических наук В.Л. Бердинский
Перунова, М. Н.
П 27 Колебания и волны: учебное пособие / М. Н. Перунова;
Оренбургский гос. ун-т – Оренбург: ОГУ, 2012. – 386 с.
ISBN
В учебном пособии представлено систематическое изложение курса «Колебания и волны». Особое внимание уделено всеобщему характеру закономерностей колебательных процессов. Все разделы иллюстрированы примерами решения задач, от простых до сложных, олимпиадных. В пособие включены тестовые задания и задачи для самостоятельного решения.
Учебное пособие предназначено для студентов, обучающихся по программам высшего профессионального образования инженерно-технических направлений подготовки.
П 
УДК 534 (07)
ББК 22.336 я 7
ÓПерунова М. Н., 2012
ÓОГУ, 2012
ISBN
Содержание
Введение……………………………………………………………………….…. 5
Глава 1 Гармонические колебания ….. ……………………………………..…. 7
§ 1 Пружинный маятник………………………………………………………..…7
§ 2 Математический маятник………………………………………………... …20
§ 3 Физический маятник……………………………………………………..…..22
§ 4 Гармонический осциллятор………………………………………………... 24
§ 5 Примеры решения задач……………………………………………..………25
§ 6 Задания для самостоятельного решения………………………………..…..41
Глава 2 Маятники в постоянных силовых полях …………………………..….69
§ 1 Пружинный маятник в постоянном силовом поле…………………….…..69
§ 2 Математический маятник в постоянном силовом поле…………………...71
§ 3 Примеры решения задач…………………………………………………..…73
§ 4 Задания для самостоятельного решения……..…………………………..…78
Глава 3 Сложение колебаний…………………………………………………....84
§ 1 Метод векторных диаграмм………………………………………………....85
§ 2 Сложение взаимно перпендикулярных колебаний…………………….…..92
§ 3 Сложение колебаний с близкими частотами, проходящими вдоль
одной прямой………………………………………………………………..……96
§ 4 Спектральное разложение……………………………………………….…..98
§ 5 Примеры решения задач……………………………………………………100
§ 6 Задания для самостоятельного решения……..……………………………104
Глава 4 Свободные электрические колебания………………………………..108
§ 1 Уравнение колебаний в контуре…………………………………………...108
§ 2 Процессы, происходящие в колебательном контуре…………………......112
§ 3 Аналогия между электрическими …………………………………….......115
§ 4 Колебательный контур с источником постоянного тока ………………..119
§ 5 Примеры решения задач……………………………………………………123
§ 6 Задания для самостоятельного решения……..……………………………136
Глава 5 Затухающие колебания………………………………………………..146
§ 1 Затухание колебаний в системах с вязким трением……………………...147
§ 2 Как быстро затухают колебания в системах с вязким трением?...............152
§ 3 Затухание колебаний в системах с сухим трением……………………….158
§ 4 Примеры решения задач……………………………………………………161
§ 5 Задания для самостоятельного решения……..……………………………168
Глава 6 Вынужденные механические колебания……………………………..175
§ 1 Вынужденная сила изменяется по гармоническому закону……………..175
§ 2 Энергетические превращения……………………………………………...181
§ 3 Несинусоидальное периодическое воздействие………………………….183
§ 4 Параметрический резонанс………………………………………………...184
§ 5 Значение резонанса…………………………………………………………188
§ 6 Примеры решения задач……………………………………………………188
§ 7 Задания для самостоятельного решения……..……………………………193
Глава 7 Вынужденные электрические колебания…………………………….200
§ 1 Переменный ток…………………………………………………………….200
§ 2 Последовательное соединение R, L, C…………………………………….216
§ 3 Резонанс токов………………………………………………………………223
§ 4 Опять о мощности в цепи переменного тока……………………………..232
§ 5 Примеры решения задач……………………………………………………236
§ 6 Задания для самостоятельного решения……..……………………………238
§ 7 Принцип действия трансформатора. Передача энергии на
расстояние ……..…………………………………………..……………………245
§ 8 Примеры решения задач……………………………………………………253
§ 9 Задания для самостоятельного решения……..……………………………257
Глава 8 Автоколебания, автоколебательные системы……………………….264
§ 1 Часы с бестиковым механизмом…………………………………………..266
§ 2 Автогенератор Ван-дер-Поля на триоде…………………………………..267
Глава 9 Упругие волны…………………………………………………………272
§ 1 Механические волны……………………………………………………….272
§ 2 Примеры решения задач……………………………………………………292
§ 3 Задания для самостоятельного решения…………………..………………292
§ 4 Звук…………………………………………………………………………..306
§ 5 Примеры решения задач……………………………………………………319
§ 6 Задания для самостоятельного решения…………………..………………326
§ 7 Интерференция волн………………………………………………………..334
§ 8 Примеры решения задач……………………………………………………348
§ 9 Задания для самостоятельного решения…………………..………………351
Глава 10 Электромагнитные волны…………………………………………...358
§ 1 Уравнения Максвелла и волновое уравнение…………………………….358
§ 2 Излучение электромагнитной волны……………………………………...368
§ 3 Энергия электромагнитной волны………………………………………...371
§ 4 Импульс электромагнитной волны………………………………………..374
§ 5 Опыты Герца………………………………………………………………..376
§ 6 Задания для самостоятельного решения…………………………………..381
Список использованных источников………………………………………….386
Введение
Колебание – это более или менее регулярно повторяющийся процесс. Таково очень нестрогое, «качественное» определение понятия «колебание». Приведем несколько примеров периодических процессов, относящихся к различным областям физики (и не только физики). Колеблется груз, подвешенный на пружине; колеблется поверхность воды; колеблется струна музыкального инструмента; колеблется давление воздуха, вызывая колебания барабанной перепонки человеческого уха; периодически изменяется солнечная активность и т.д.
Кроме того, более или менее периодически меняется температура воздуха в течение года; периодически изменяется количеств автомобилей на улицах города (больше в часы пик - меньше поздней ночью); периодически изменяется экономическая ситуация в жизни общества - кризисные явления сменяются подъемами экономики и т.д.
По существу периодические процессы – это наиболее часто встречающие процессы в природе, а закономерности колебательных процессов – фундаментальные законы природы.
Наша задача – познакомиться с наиболее простейшими видами колебательного движения, основными характеристиками колебательных процессов, с математическим способом описания колебаний.
Время, через которое движение полностью повторяется, называется периодом Т. Число колебаний, совершаемых в единицу времени – частота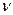 
. Очевидно, 
.
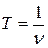Колебания можно классифицировать различными способами. По причине, вызывающей колебания, их можно разделить на свободные и вынужденные.
Свободные колебания происходят под действием внутренних сил, возникающих в системе при выведении ее из положения равновесия. Таковы колебания груза, подвешенного на пружине – достаточно вывести маятник из положения равновесия и больше не «вмешиваться» в его поведение, груз будет периодически изменять свое положение в пространстве.
Вынужденные колебания происходят под действием внешней периодически действующей силы. Например, вибрирует опора станка под действие регулярных толчков со стороны вращающихся деталей; колеблется корпус музыкального инструмента и столб воздуха внутри него под действием толчков со стороны прикрепленной к корпусу колеблющейся струны.
Другой способ классификации колебательных процессов основан на сравнении законов, по которым происходит изменение колеблющейся величины. Если какая-либо физическая величина изменяется по гармоническому закону (закону синуса или косинуса), то колебания называют гармоническими. Любые другие периодические изменения называются негармоническими. Заметим, что гармоническими могут быть как свободные, так и вынужденные колебания.
Глава 1 Гармонические колебания
§1 Пружинный маятник
Дифференциальное уравнение гармонических колебаний
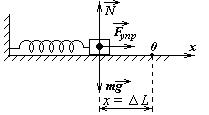Пружинный маятник – система, состоящая из пружины и прикрепленного к ней груза. Система располагается на горизонтальной поверхности. Рассмотрим идеальный случай, когда поверхность, по которой двигается груз, гладкая. Отсутствие трения в системе означает, что энергия, сообщенная системе при выведении ее из положения равновесия, будет сохраняться, не переходя во внутреннюю.
Выберем ноль на оси ОХ, вдоль которой колеблется груз, в положении недеформированной пружины. Такой выбор нуля позволяет приравнять координату тела х и деформацию пружины ΔL: x = Δ L.
Запишем второй закон Ньютона для груза, выведенного из положения равновесия:
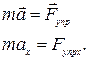
Согласно закону Гука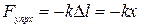 
, а проекция ускорения – вторая производная от координаты тела по времени 
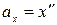. Тогда
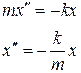(1)
Введем обозначение
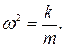
С учетом этого обозначения уравнение (1) примет вид
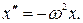(2)
Получили дифференциальное уравнение, содержащее функцию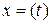 
и ее вторую производную, причем вторая производная прямо пропорциональна самой функции, взятой с противоположным знаком.
Решением дифференциального уравнения (2) является функция вида
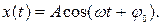(3)
Физический смысл констант А, ω, φ0 выясним, исходя из свойств гармонической функции.
а) Функция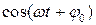 
ограниченная, ее максимальное значение равно 1. Когда косинус принимает максимальное значение, равное единице, отклонение тела от положения равновесия тоже принимает максимальное значение 
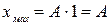. Таким образом, А - максимальное отклонение груза от положения равновесия – амплитуда.
б) Функция 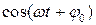периодическая, ее значение повторяется при изменении аргумента на 2π. С другой стороны, движение полностью повторяется через время, равное периоду колебаний Т. Тогда нетрудно видеть, что через время, равное периоду, аргумент косинуса изменяется на 2π:
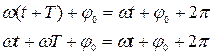
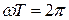(4)
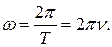
Величину ω, отличающуюся от обычной частоты ν в 2π раз, называют циклической частотой. Циклическая частота ω – величина, численно равная числу колебаний, совершаемых за 2π секунды.
в) Аргумент косинуса называют фазой φ. В момент начала колебаний t = 0 аргумент косинуса становится равным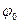 
; поэтому величину 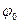называют начальной фазой колебаний. Фаза измеряется в радианах.
Кинематика гармонических колебаний
Поговорим подробнее о фазе. Фаза колебаний полностью определяет состояние колебательной системы в рассматриваемый момент времени – зная фазу, можно рассчитать координату, скорость, ускорение тела, кинетическую и потенциальную энергию, силу, действующую на тело.
Покажем это. По определению проекция скорости – это первая производная от координаты тела по времени:
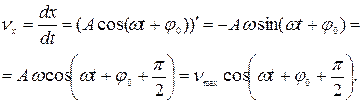
Видим, что скорость пружинного маятника, совершающего гармонические колебания, тоже меняется по гармоническому закону. Но аргумент функции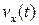 
в любой момент времени больше аргумента функции 
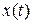на π/2. В этом случае говорят, что скорость колеблющегося тела опережает координату по фазе на π/2.
Проекция ускорения – первая производная от проекции скорости и вторая производная от координаты:
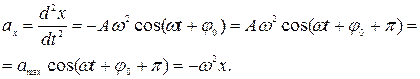
Фаза ускорения отличается от фазы координаты на π радиан – в этом случае говорят, что ускорение и координата колеблются в противофазе.
Зная деформацию пружины, скорость и ускорение колеблющегося тела, можно рассчитать его кинетическую и потенциальную энергии и силу, действующую на него:
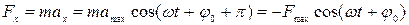
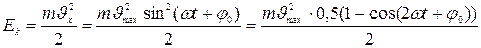
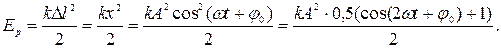
Видим, что обе энергии, кинетическая и потенциальная, тоже меняются по гармоническому закону, только с удвоенной частотой.
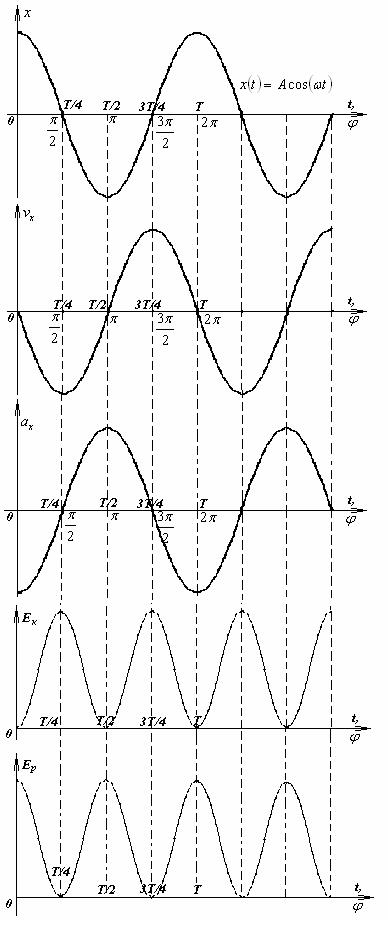
Подведем некоторые итоги
Мы показали, что пружинный маятник, будучи выведенными из положения равновесия, совершает колебания, при которых все кинематические характеристики движения (координата, скорость, ускорение), сила, кинетическая и потенциальная энергии меняются по закону синуса или косинуса. Поэтому колебания пружинного маятника и называются гармоническими.
Осталось выяснить, от чего зависит численные значения констант А - амплитуды, ω – циклической частоты , φ0 - начальной фазы , входящих в уравнение движения колеблющегося тела (3).
Константа ω – циклическая частота – появилась в дифференциальном уравнении, когда мы ввели обозначение:
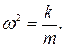
Видим, что циклическая частота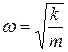 
зависит только от свойств самой колебательной системы. В случае пружинного маятника она зависит от жесткости пружины и массы прикрепленного к ней груза. Зная циклическую частоту на основании формулы (4), можем рассчитать период колебаний пружинного маятника 
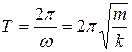. Он не зависит от размаха колебаний (только бы выполнялся закон Гука!), от способа выведения маятника из положения равновесия. Для данной пружины и данного груза период колебаний всегда одинаков!
Амплитуда колебаний зависит от энергии, сообщенной пружинному маятнику при выведении его из положения. Очевидно, в крайнем положении деформация пружины максимальна и равна амплитуде колебаний А. Полная энергия колебательной системы в этот момент состоит только из потенциальной энергии деформированной пружины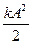 
, кинетическая энергия в этот момент отсутствует, ибо в крайнем положении маятник остановился.
Тогда
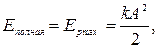
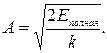
Начальная фаза зависит от того, каким образом маятник вывели из положения равновесия. Например, маятник отклонили от положения равновесия на расстояние А и отпустили без начальной скорости. Запишем уравнение движения колеблющегося тела и учтем тот факт, что в начальный момент координата тела равна А:
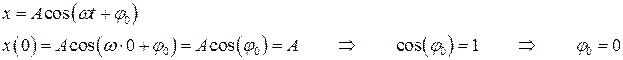
Уравнение движения маятника, выведенного из положения равновесия таким способом, выглядит просто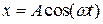 
.
Другая ситуация – маятник привели в колебания, толкнув его в положении равновесия. Тогда начальная координата тела равна нулю:
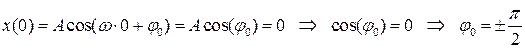
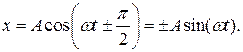Уравнение движения маятника тогда будет выглядеть следующим образом:
Знак, плюс или минус, зависит от выбора положительного направления оси 0Х. Если направление оси 0Х совпадает с направлением начальной скорости, то в уравнении движения будет знак плюс, и наоборот.
Динамика гармонических колебаний пружинного маятника
Рассмотрим процессы, происходящие в процессе колебаний пружинного маятника.
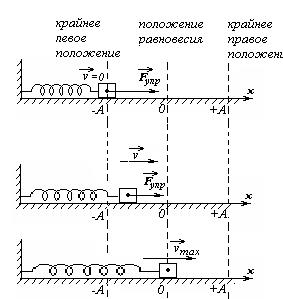В крайнем положении деформация пружины максимальна, следовательно, сила упругости, ускорение и потенциальная энергия деформированной пружины тоже максимальны. Скорость груза и кинетическая энергия равны нулю. Полная энергия системы состоит только из потенциальной энергии деформации пружины.
Первая четверть периода.
Пружина распрямляется, ее деформация уменьшается. Следовательно, уменьшается величина силы упругости и ускорения груза. Потенциальная энергия деформированной пружины уменьшается, переходя в кинетическую. Модуль скорости груза увеличивается.
Маятник проходит положение равновесия. В этом положении пружина не деформирована, значит, сила упругости обращается в ноль (это и есть условие равновесия). Согласно второму закону Ньютона ускорение тоже обращается в ноль. Потенциальная энергия деформации пружины перешла в кинетическую, этот вид энергии принимает максимальное значение. Скорость груза достигла максимального значения.
Вследствие своей инертности маятник не может изменить свою скорость мгновенно, он проскакивает положение равновесия. Начинается вторая четверть периода.
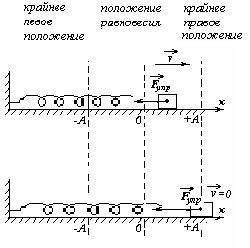Груз удаляется от положения равновесия, растягивая пружину. Сила упругости, изменившая свое направление, растет по модулю. Увеличивается потенциальная энергия упругой деформации пружины. Кинетическая энергия и скорость груза уменьшаются.
Груз удаляется от положения равновесия пока не остановится. В крайнем положении кинетическая энергия груза обращается в ноль, она полностью перешла в потенциальную энергию упругой деформации. Деформация пружины максимальна, модуль силы упругости и ускорения приняли наибольшее значение. Нетрудно видеть, что отклонения груза от положения в обе стороны одинаковы.
Вторая половина периода происходит аналогично.
Подведем итоги
В крайнем положении – это точки остановки маятника – скорость и кинетическая энергия маятника равны нулю. Отклонение маятника от положения равновесия максимально (и равно амплитуде). Деформация пружины максимальна, модуль силы упругости, ускорения и потенциальная энергия упругой деформации пружины максимальны. Полная энергия системы состоит только из потенциальной энергии.
В положении равновесия сила, под действием которой происходят колебания, обращается в ноль. Согласно второму закону Ньютона ускорение тоже обращается в ноль. Скорость и кинетическая энергия максимальна. Потенциальная энергия минимальна.
При переходе из крайнего положения в положение равновесия скорость и кинетическая энергия груза растут, а деформация пружины, модуль силы, ускорения и потенциальная энергия систему уменьшаются.
В процессе движения из положения равновесия в крайнее положение растут деформация пружины, модуль силы упругости и ускорения, потенциальная энергия упругой деформации. Скорость и кинетическая энергия груза уменьшаются (таблица 1).
Таблица 1
| Крайнее положение |  | Положение равновесия |  | Крайнее положение | |
| Отклонение от положения равновесия | Мах | Уменьшается | Увеличивается | Мах | |
| Деформация пружины | Мах | Уменьшается | Увеличивается | Мах | |
| Модуль силы упругости | Мах | Уменьшается | Увеличивается | Мах | |
| Модуль ускорения | Мах | Уменьшается | Увеличивается | Мах | |
| Модуль скорости | Увеличивается | Мах | Уменьшается | ||
| Кинетическая энергия | Уменьшается | Мах | Уменьшается | ||
| Потенциальная энергия | Мах | Уменьшается | Min | Увеличивается | Мах |
Фазовая траектория*
Состояние частицы полностью характеризуется заданием ее координат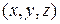 
и скоростей 
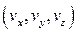. Почему? Координаты тела определяют потенциальную энергию взаимодействия тела с другими телами, а скорости – импульс тела и его кинетическую энергию. Именно поэтому хочется иметь наглядное изображение движения тела, в нашем случае маятника, позволяющее «увидеть» состояние колебательной системы в любой момент времени.
Задача решается несложно, если в декартовой системе координат по оси абсцисс откладывать координату тела, а по оси ординат – соответствующую проекцию скорости. Такая координатная плоскость называется фазовой плоскостью. Состояние тела на фазовой плоскости задается изображающей точкой, координаты которо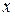й 
и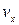 
. С течение времени 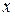и 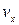тела изменяются, следовательно, точка, изображающая состояние тела на фазовой плоскости, перемещается, описывая так называемую фазовую траекторию.
В случае гармонического осциллятора координата и проекция скорости тела изменяются с течением времени следующим образом
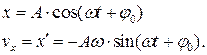
Отсюда несложно получить уравнение фазовой траектории:
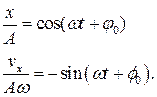
Возведем обе части каждого уравнения в квадрат и сложим:
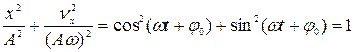
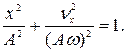(5)
Это уравнение эллипса с полуосями А и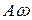 
. Фазовая траектория гармонического осциллятора выглядит следующим образом:
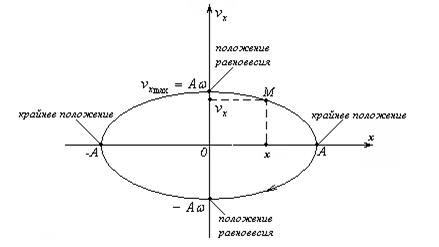
То, о чем мы говорили ранее, теперь стало наглядно. Явно видно, что движение тела ограничено в пространстве – оно колеблется на отрезке от –А до А. Проекция скорости тела тоже принимает ограниченные значения от - 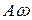до .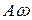
Вспомним, что амплитуда колеблющегося тела определяется энергией, сообщенной системе при выведении ее из положения равновесия:
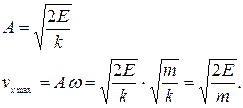
Очевидно, что сообщение колебательной системе большей энергии при выведении ее из положения равновесия приведет к увеличению амплитуды колебаний и максимального значения скорости. Фазовая траектория по-прежнему останется эллипсом, пропорционально увеличатся
только его полуоси. Мы получаем семейство фазовых траекторий, отличающихся амплитудой колебаний вследствие отличия энергий, сообщенных системе.
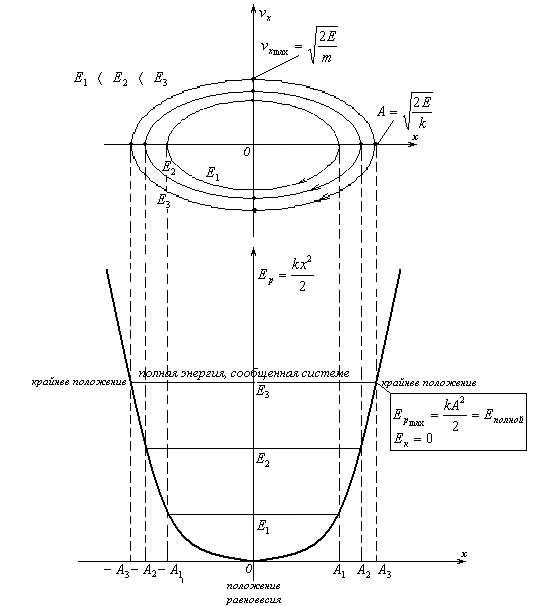
По существу, фазовая траектория - это наглядное изображение закона сохранения механической энергии.
Нетрудно показать, что выражение для закона сохранения энергии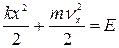 
преобразуется к виду (5). Для этого достаточно обе части равенства разделить на Е и вспомнить связь между полной энергией системы и амплитудой колебаний:
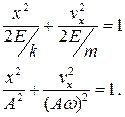
Если энергию колебательной системы каким-либо образом увеличивать, размах колебаний будет возрастать – колебания будут «раскачиваться». Фазовая траектория при этом будет «раскручиваться».
Если по каким-либо причинам энергия колебательной системы будет уменьшаться, размах колебаний будет уменьшаться. В этом случае колебания будут затухать. Фазовая траектория будет все больше «скручиваться».
§2 Математический маятник
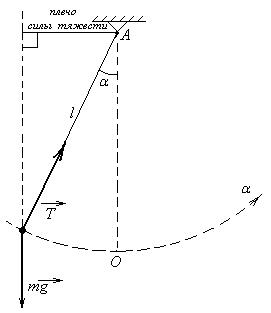Математическим маятником называют материальную точку массы m, подвешенную на нерастяжимой нити длины l. При выведении из положения равновесия маятник начинает качаться, совершать колебательное движение. Траекторией груза при этом будет дуга окружности.
Запишем основной закон вращательного движения:
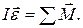
Учтем, что по определению угловое ускорение ε – вторая производная от угла поворота α, а вращающий момент относительно точки А создает только сила тяжести:
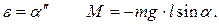
Знак «-» делает момент силы тяжести положительным, что соответствует ситуации на рисунке, ибо угол отклонения маятника отрицателен. Тогда с учетом малости угла отклонения маятника от положения равновесия (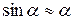 
) получаем
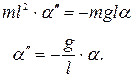
Обозначим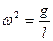 
. Окончательно получаем дифференциальное уравнение
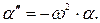
Это не что иное, как уравнение гармонических колебаний. Следовательно, математический маятник при отклонении на малые углы от положения равновесия будет совершать гармонические колебания с периодом
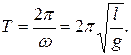
§3 Физический маятник
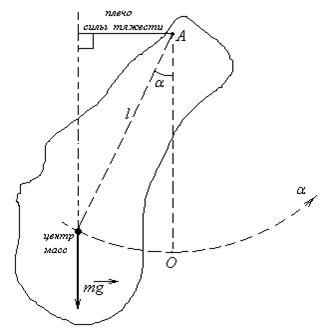Физический маятник – это любое тело с закрепленной осью вращения, не совпадающей с центром масс.
Пусть тело закреплено в точке А и может свободно вращаться относительной этой точки. Центр масс тела находится на расстоянии l от точки закрепления. Нетрудно видеть, что при выведении тела из положения равновесия его центр масс будет двигаться по дуге окружности радиуса l.
Поскольку сила реакции опоры, действующая в точке закрепления, вращающего момента не создает, второй закон Ньютона для вращательного движения будет выглядеть так:
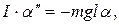
где I – момент инерции тела относительно точки А. Преобразуем полученное выражение
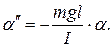
Введя обозначение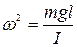 
, получаем уже известное дифференциальное уравнение гармонических колебаний 
.
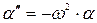Итак, при малых углах отклонения от положения равновесия физический маятник совершает гармонические колебания с периодом .
Приведенная длина физического маятника
Сравним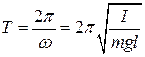 
периоды колебаний физического и математического маятников.
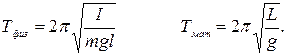
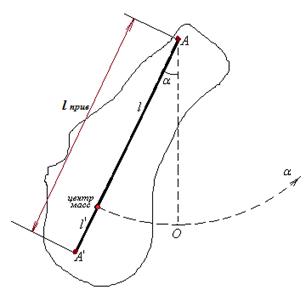
Величина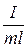 
имеет размерность длины. Введем обозначение 
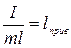, где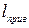 
- приведенная длина физического маятника. Понятно, что приведенная длина 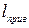- это длина такого математического маятника, период колебаний которого совпадает с периодом физического маятника. Приведенная длина не совпадает с расстоянием от точки подвеса до центра масс 
( 
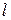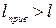)! При изменении положения оси вращения маятника будет меняться и приведенная длина.
Приведенная длина интересна тем, что при переносе точки подвеса маятника в точку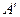 
период колебаний маятника не изменяется. Покажем это.
Приведенная длина исходного маятника
(*)
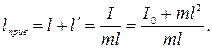Расстояние от новой точки подвеса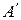 
до центра масс равно 
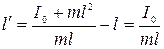. После переворота приведенная длина получившегося маятника будет равна 
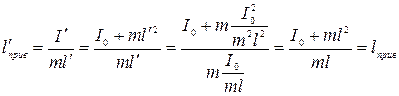. Видим, что приведенная длина перевернутого маятника совпала с приведенной длиной исходного маятника, следовательно периоды колебаний маятников одинаковы.
§ 4 Гармонический осциллятор
Пора сделать некоторые обобщения. Мы рассмотрели только три примера колебательных систем из области механики, но их можно привести десятки, причем из разных областей физики.
Очевидно, что в любой физической системе, поведение которой подчиняется дифференциальному уравнению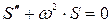 
будут наблюдаться гармонические колебания величины S. В этом случае систему называют гармоническим осциллятором.
Физические различия между гармоническими осцилляторами в конечном счете будут проявляться в том, что параметр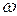 
, названный нами циклической частотой, определяется различными физическими величинами. В случае пружинного маятника циклическая частота определяется жесткостью пружины k и массой груза m: 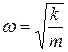. В случае математического маятника циклическая частота зависит от длины подвеса и ускорения свободного падения 
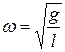, для физического маятника 
.
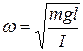Однако, есть одно важное обстоятельство, которое объединяет поведение всех этих физически различных колебательных систем! Каждый раз система, будучи выведенной из положения равновесия, отвечает на это возникновением силы (или вращающего момента), стремящейся вернуть систему в положение равновесия. Причем величина этой силы или вращающего момента пропорциональна величине смещения тела от положения равновесия. Это общее свойство всех гармонических осцилляторов. Силу вида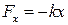 
, независимо от её природы, называют квазиупругой.
С математической точки зрения уравнения, описывающие любой гармонический осциллятор, абсолютно тождественны! Это дает нам право утверждать, что физические закономерности любого гармонического колебания, независимо от его природы, тоже тождественны. Эти закономерности мы и рассмотрели на примере пружинного маятника.
§ 5 Примеры решения задач
Задача1 Читаем уравнение гармонических колебаний
Зависимость координаты тела от времени имеет вид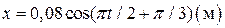 
. Определите характер движения тела.
Решение:
· Функция 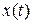меняется по закону косинуса, следовательно, тело совершает гармонические колебания.
· 
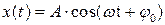Сопоставим уравнение движения тела с уравнением колебательного движения.
· Видим, что амплитуда колебаний равна А = 0,08 м.
· Множитель, стоящий в уравнении движения перед временем, - циклическая частота. В нашем случае она равна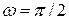 
с-1.
· Тогда частота колебаний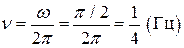 
.
Период колебаний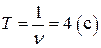 
.
· 
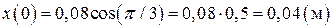Начальная фаза колебаний 
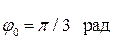. Зная начальную фазу, можно определить, каким образом маятник привели в колебательное движение.
Проекция скорости – производная от координаты по времени.
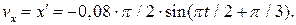
Проекция начальной скорости
.
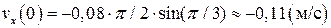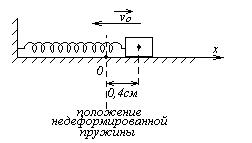Для возбуждения колебаний маятник отклонили от положения равновесия на 4 см и толкнули, сообщив скорость 0,11 м/с.
· Проекция ускорения – производная от проекции скорости
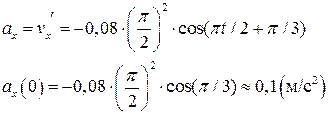
· Максимальные значения скорости и ускорения
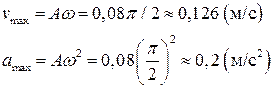
Задача 2 Составляем уравнение движения
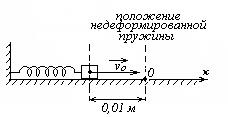Груз массой 400 г прикреплен к пружине жесткостью 40 Н/м. Пружину сжали на 1 см и толкнули груз к положению равновесия, сообщив грузу скорость 0,1 м/с. Составьте уравнение движения пружинного маятника.
Решение:
Введем систему координат, расположив ось ОХ вдоль траектории маятника. Ноль на оси ОХ поместим в положение недеформированной пружины, при таком выборе нуля координата груза и деформация пружины совпадают. Направим ось координат в сторону растяжения пружины.
Уравнение движения колеблющегося тела выглядит следующим образом
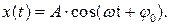
· Циклическая частота определяется параметрами колебательной системы
· 
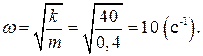
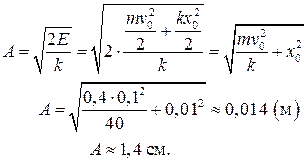Амплитуда колебаний зависит от энергии, сообщенной системе при выведении ее из положения равновесия. Полная механическая энергия в начальный момент времени равна 
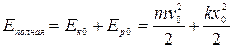. Тогда амплитуда колебаний
· Начальная фаза может быть найдена из начальных условий.
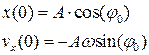
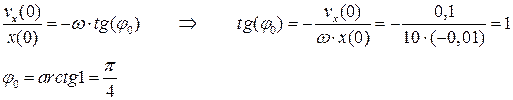
Окончательный результат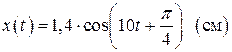 
Задача 3 Уравнение, связывающее координату и скорость колеблющегося тела
При смещении точки от положения равновесия 5 см скорость точки 6 см/с, а при смещении 3 см скорость точки 10 см/с. Найдите амплитуду и частоту колебаний.
Решение: